Risonanza elettrica
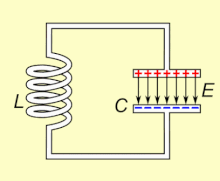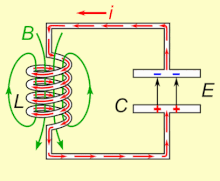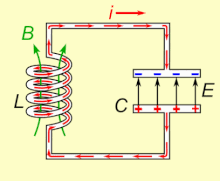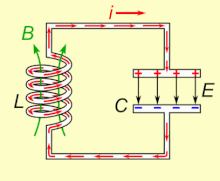
In un circuito a corrente alternata, la risonanza elettrica è un fenomeno stazionario che si manifesta ad una frequenza in cui la reattanza capacitiva 1/ωC e la reattanza induttiva ωL sono di uguale modulo, costringendo l'energia ad oscillare tra il campo magnetico di un induttore ed il campo elettrico di un condensatore.
Spiegazione[modifica | modifica wikitesto]
La risonanza si instaura allorché, considerando un circuito chiuso e senza perdite, il campo magnetico presente nell'induttanza genera, per via del suo naturale decadimento, una corrente elettrica autoindotta nel proprio avvolgimento che, scorrendo attraverso il circuito chiuso, carica il condensatore; a sua volta il condensatore, scaricandosi, fornisce la corrente elettrica che, attraverso l'avvolgimento dell'induttore, rigenera il campo magnetico iniziale nello stesso: ripetendosi indefinitamente tale processo, si assiste all'instaurarsi del fenomeno della risonanza. Il pendolo meccanico ne è una analogia.
Condizioni di risonanza[modifica | modifica wikitesto]
Alla risonanza, l'impedenza Z data dalla somma della reattanza induttiva e di quella capacitiva poste in serie raggiunge il suo minimo. L'ammettenza Y delle due reattanze poste in parallelo raggiunge invece il suo massimo. Nel caso di risuonatore in serie, l'impedenza è data dalla seguente espressione:
Mentre nel caso di risuonatore in parallelo:
in cui:
- ω è la pulsazione
- L è l'induttanza
- C è la capacità
- R è la resistenza parassita (ad esempio la resistenza parassita in serie all'induttanza dovuta al filo dell'avvolgimento con cui è realizzata nel caso di un risuonatore parallelo)
Pulsazione di risonanza[modifica | modifica wikitesto]

Quando, alla pulsazione di risonanza, il modulo della reattanza induttiva è uguale a quello della reattanza capacitiva l'impedenza diventa minima nel caso della serie e massima nel caso del parallelo.
La pulsazione per la quale le due reattanze si uguagliano in modulo è data, per entrambi i casi di risuonatore serie e risuonatore parallelo, dalla seguente espressione:
Tale pulsazione corrisponde alla pulsazione naturale di oscillazione nel caso di assenza di perdite (e quindi smorzamento nullo; in tal caso si ha un risuonatore ideale, caratterizzato da: nel caso serie; nel caso parallelo). Nella realtà le perdite sono sempre presenti (e il risuonatore si dice quindi "smorzato") a causa di componenti cosiddette "parassite" sempre presenti nei circuiti reali; esse portano ad una frequenza naturale di oscillazione differente (in particolare, "inferiore") da quella ideale precedentemente calcolata. Tale differenza sarà piccola in caso di basse perdite (i.e. fattore di merito Q elevato). In un circuito reale, caratterizzato pertanto da "perdite" che determinano il cosiddetto "smorzamento", la frequenza naturale del risuonatore serie vale:
Mentre nel caso di risuonatore parallelo vale:
È possibile esprimere elegantemente, con un'equazione valida per entrambi i casi serie e parallelo, la frequenza naturale dell'oscillatore smorzato in funzione del suo fattore di merito Q (detto anche fattore di qualità) e della frequenza naturale in assenza di smorzamento:
dove per il caso serie il fattore di merito è dato da:
mentre per il caso parallelo da:
Alla pulsazione di risonanza fa riscontro la frequenza di risonanza che è evidentemente
Frequenza di risonanza[modifica | modifica wikitesto]
Utilizzo[modifica | modifica wikitesto]
La risonanza viene utilizzata nei radioricevitori ad amplificazione accordata, negli amplificatori accordati, nei filtri accordati ed altri dispositivi che, in generale, devono operare prevalentemente con segnali caratterizzati da pulsazioni assegnate ed appartenenti ad un predefinito intervallo di valori.
Voci correlate[modifica | modifica wikitesto]
Altri progetti[modifica | modifica wikitesto]
 Wikizionario contiene il lemma di dizionario «risonanza elettrica»
Wikizionario contiene il lemma di dizionario «risonanza elettrica»











