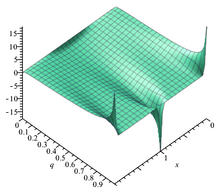
Funzione Theta originale di Jacobi, θ1 con u = iπz e con nome q = eiπτ = 0.1e0.1iπ Jacobi theta 1 Jacobi theta 2 In matematica , le funzioni theta di Jacobi sono funzioni speciali utili in analisi complessa .
Le funzioni
ϑ
1
(
z
,
q
)
,
ϑ
2
(
z
,
q
)
,
ϑ
3
(
z
,
q
)
,
ϑ
4
(
z
,
q
)
{\displaystyle \vartheta _{1}(z,q),\vartheta _{2}(z,q),\vartheta _{3}(z,q),\vartheta _{4}(z,q)}
Carl Gustav Jakob Jacobi nella teoria delle funzioni ellittiche nel 1829 . Sono rispettivamente definite con le serie :
θ
1
(
z
,
q
)
=
2
q
1
/
4
∑
n
=
0
∞
(
−
1
)
n
q
n
(
n
+
1
)
sin
(
(
2
n
+
1
)
z
)
,
{\displaystyle \theta _{1}(z,q)=2q^{1/4}\sum _{n=0}^{\infty }(-1)^{n}q^{n(n+1)}\sin {\big (}(2n+1)z{\big )},}
θ
2
(
z
,
q
)
=
ϑ
10
(
z
,
q
)
=
2
q
1
/
4
∑
n
=
0
∞
q
n
(
n
+
1
)
cos
(
(
2
n
+
1
)
z
)
,
{\displaystyle \theta _{2}(z,q)=\vartheta _{10}(z,q)=2q^{1/4}\sum _{n=0}^{\infty }q^{n(n+1)}\cos {\big (}(2n+1)z{\big )},}
θ
3
(
z
,
q
)
=
ϑ
00
(
z
,
q
)
=
1
+
2
∑
n
=
1
∞
q
n
2
cos
(
2
n
z
)
,
{\displaystyle \theta _{3}(z,q)=\vartheta _{00}(z,q)=1+2\sum _{n=1}^{\infty }q^{n^{2}}\cos(2nz),}
θ
4
(
z
,
q
)
=
ϑ
01
(
z
,
q
)
=
1
+
2
∑
n
=
1
∞
(
−
1
)
n
q
n
2
cos
(
2
n
z
)
,
{\displaystyle \theta _{4}(z,q)=\vartheta _{01}(z,q)=1+2\sum _{n=1}^{\infty }(-1)^{n}q^{n^{2}}\cos(2nz),}
dove
q
=
e
π
i
τ
{\displaystyle q=e^{\pi i\tau }}
τ
{\displaystyle \tau }
semipiano superiore complesso , cioè
τ
{\displaystyle \tau }
numero complesso con parte immaginaria positiva, e quindi
|
q
|
<
1
{\displaystyle |q|<1}
piano complesso , cioè per ogni
z
∈
C
{\displaystyle z\in \mathbb {C} }
L'importanza delle funzioni theta di Jacobi nella teoria delle funzioni ellittiche viene dalla possibilità di esprimere tutte le funzioni ellittiche di Jacobi come rapporto di due funzioni theta (vedi le formule 16.36.3-16.36.7 di Abramowitz e Stegun, e la prova di Whittaker e Watson).
Per
z
=
0
,
{\displaystyle z=0,}
ϑ
00
(
q
)
{\displaystyle \vartheta _{00}(q)}
ϑ
01
(
q
)
{\displaystyle \vartheta _{01}(q)}
ϑ
10
(
q
)
{\displaystyle \vartheta _{10}(q)}
ϑ
00
(
q
)
=
∑
k
=
−
∞
∞
q
k
2
,
{\displaystyle \vartheta _{00}(q)=\sum _{k=-\infty }^{\infty }q^{k^{2}},}
ϑ
01
(
q
)
=
ϑ
00
(
−
q
)
=
∑
k
=
−
∞
∞
(
−
1
)
k
q
k
2
,
{\displaystyle \vartheta _{01}(q)=\vartheta _{00}(-q)=\sum _{k=-\infty }^{\infty }(-1)^{k}q^{k^{2}},}
ϑ
10
(
q
)
=
∑
k
=
−
∞
∞
q
(
k
+
1
2
)
2
.
{\displaystyle \vartheta _{10}(q)=\sum _{k=-\infty }^{\infty }q^{{\big (}k+{\tfrac {1}{2}}{\big )}^{2}}.}
Inoltre vale la seguente relazione detta identità di Jacobi:
ϑ
00
(
q
)
4
=
ϑ
10
(
q
)
4
+
ϑ
01
(
q
)
4
.
{\displaystyle \vartheta _{00}(q)^{4}=\vartheta _{10}(q)^{4}+\vartheta _{01}(q)^{4}.}
Le seguenti formule esprimono la relazione delle funzioni theta con la funzione lambda ellittica:
ϑ
00
(
exp
(
−
π
w
)
)
=
∑
a
=
−
∞
∞
exp
(
−
a
2
π
w
)
=
(
∑
a
=
−
∞
∞
sech
(
a
π
w
)
)
1
/
2
=
2
π
−
1
K
(
λ
∗
(
w
)
)
,
{\displaystyle \vartheta _{00}{\big (}\exp(-\pi {\sqrt {w}}){\big )}=\sum _{a=-\infty }^{\infty }\exp(-a^{2}\pi {\sqrt {w}})=\left(\sum _{a=-\infty }^{\infty }\operatorname {sech} (a\pi {\sqrt {w}})\right)^{1/2}={\sqrt {2\pi ^{-1}K{\big (}\lambda ^{*}(w){\big )}}},}
ϑ
10
(
exp
(
−
π
w
)
)
=
∑
a
=
−
∞
∞
exp
(
−
(
a
+
1
2
)
2
π
w
)
=
(
∑
a
=
−
∞
∞
sech
(
(
a
+
1
2
)
π
w
)
)
1
/
2
=
2
π
−
1
λ
∗
(
w
)
K
(
λ
∗
(
w
)
)
=
2
λ
∗
(
4
w
)
4
π
−
1
K
(
λ
∗
(
4
w
)
)
,
{\displaystyle \vartheta _{10}{\big (}\exp(-\pi {\sqrt {w}}){\big )}=\sum _{a=-\infty }^{\infty }\exp \left(-(a+{\tfrac {1}{2}})^{2}\pi {\sqrt {w}}\right)=\left(\sum _{a=-\infty }^{\infty }\operatorname {sech} \left((a+{\tfrac {1}{2}})\pi {\sqrt {w}}\right)\right)^{1/2}={\sqrt {2\pi ^{-1}\lambda ^{*}(w)K{\big (}\lambda ^{*}(w){\big )}}}=2{\sqrt[{4}]{\lambda ^{*}(4w)}}{\sqrt {\pi ^{-1}K{\big (}\lambda ^{*}(4w){\big )}}},}
ϑ
01
(
exp
(
−
π
w
)
)
=
∑
a
=
−
∞
∞
(
−
1
)
a
exp
(
−
a
2
π
w
)
=
2
π
−
1
λ
∗
(
1
/
w
)
K
(
λ
∗
(
w
)
)
,
{\displaystyle \vartheta _{01}{\big (}\exp(-\pi {\sqrt {w}}){\big )}=\sum _{a=-\infty }^{\infty }(-1)^{a}\exp(-a^{2}\pi {\sqrt {w}})={\sqrt {2\pi ^{-1}\lambda ^{*}(1/w)K{\big (}\lambda ^{*}(w){\big )}}},}
dove
K
{\displaystyle K}
integrale ellittico completo di prima specie e vale la relazione:
K
(
1
−
λ
∗
(
w
)
2
)
K
(
λ
∗
(
w
)
)
=
w
.
{\displaystyle {\frac {K\left({\sqrt {1-\lambda ^{*}(w)^{2}}}\right)}{K{\big (}\lambda ^{*}(w){\big )}}}={\sqrt {w}}.}
Tabella dei valori:
q
ϑ₁₀(q)
ϑ₀₁(q)
ϑ₀₀(q)
exp(-π)
G
{\displaystyle {\sqrt {G}}}
G
{\displaystyle {\sqrt {G}}}
2
1
/
4
G
{\displaystyle 2^{1/4}{\sqrt {G}}}
exp(-2π)
2
−
1
/
2
2
−
1
G
{\displaystyle 2^{-1/2}{\sqrt {{\sqrt {2}}-1}}{\sqrt {G}}}
2
1
/
8
G
{\displaystyle 2^{1/8}{\sqrt {G}}}
2
−
1
/
2
2
+
1
G
{\displaystyle 2^{-1/2}{\sqrt {{\sqrt {2}}+1}}{\sqrt {G}}}
exp(-3π)
2
−
5
/
4
3
−
3
/
8
3
−
1
(
3
+
1
−
12
4
)
G
{\displaystyle 2^{-5/4}3^{-3/8}{\sqrt {{\sqrt {3}}-1}}({\sqrt {3}}+1-{\sqrt[{4}]{12}}){\sqrt {G}}}
2
−
5
/
4
3
−
3
/
8
3
−
1
(
3
+
1
+
12
4
)
G
{\displaystyle 2^{-5/4}3^{-3/8}{\sqrt {{\sqrt {3}}-1}}({\sqrt {3}}+1+{\sqrt[{4}]{12}}){\sqrt {G}}}
3
−
3
/
8
3
+
1
G
{\displaystyle 3^{-3/8}{\sqrt {{\sqrt {3}}+1}}{\sqrt {G}}}
exp(-4π)
2
−
1
(
2
4
−
1
)
G
{\displaystyle 2^{-1}({\sqrt[{4}]{2}}-1){\sqrt {G}}}
2
−
3
/
16
2
+
1
4
G
{\displaystyle 2^{-3/16}{\sqrt[{4}]{{\sqrt {2}}+1}}{\sqrt {G}}}
2
−
1
(
2
4
+
1
)
G
{\displaystyle 2^{-1}({\sqrt[{4}]{2}}+1){\sqrt {G}}}
exp(-5π)
2
−
3
/
2
5
−
1
/
2
5
−
1
(
5
4
−
1
)
2
G
{\displaystyle 2^{-3/2}5^{-1/2}{\sqrt {{\sqrt {5}}-1}}({\sqrt[{4}]{5}}-1)^{2}{\sqrt {G}}}
2
−
3
/
2
5
−
1
/
2
5
−
1
(
5
4
+
1
)
2
G
{\displaystyle 2^{-3/2}5^{-1/2}{\sqrt {{\sqrt {5}}-1}}({\sqrt[{4}]{5}}+1)^{2}{\sqrt {G}}}
2
1
/
4
5
−
1
/
2
5
+
2
G
{\displaystyle 2^{1/4}5^{-1/2}{\sqrt {{\sqrt {5}}+2}}{\sqrt {G}}}
dove
G
{\displaystyle G}
costante di Gauss e questa costante è il reciproco della media aritmetico-geometrica tra 1 e
2
{\displaystyle {\sqrt {2}}}
Altre relazioni importanti per l'aritmetica:
ϑ
10
(
q
)
2
=
2
ϑ
10
(
q
2
)
ϑ
00
(
q
2
)
;
{\displaystyle \vartheta _{10}(q)^{2}=2\vartheta _{10}(q^{2})\vartheta _{00}(q^{2});}
ϑ
00
(
q
)
+
ϑ
01
(
q
)
=
2
ϑ
00
(
q
4
)
;
{\displaystyle \vartheta _{00}(q)+\vartheta _{01}(q)=2\vartheta _{00}(q^{4});}
ϑ
00
(
q
4
)
+
ϑ
10
(
q
4
)
=
ϑ
00
(
q
)
;
{\displaystyle \vartheta _{00}(q^{4})+\vartheta _{10}(q^{4})=\vartheta _{00}(q);}
ϑ
00
(
exp
(
−
π
/
y
)
)
=
y
ϑ
00
(
exp
(
−
π
y
)
)
;
{\displaystyle \vartheta _{00}{\big (}\exp(-\pi /y){\big )}={\sqrt {y}}\,\vartheta _{00}{\big (}\exp(-\pi y){\big )};}
n
ϑ
00
(
exp
(
−
n
π
w
)
)
2
ϑ
00
(
exp
(
−
π
w
)
)
2
=
∑
k
=
1
n
dn
(
2
k
n
K
(
λ
∗
(
w
)
)
;
λ
∗
(
w
)
)
.
{\displaystyle {\frac {n\vartheta _{00}{\big (}\exp(-n\pi {\sqrt {w}}){\big )}^{2}}{\vartheta _{00}{\big (}\exp(-\pi {\sqrt {w}}){\big )}^{2}}}=\sum _{k=1}^{n}\operatorname {dn} \left({\frac {2k}{n}}K{\big (}\lambda ^{*}(w){\big )};\lambda ^{*}(w)\right).}
L'abbreviazione
dn
{\displaystyle \operatorname {dn} }
funzione ellittica di Jacobi Delta Amplitudinis.
Somma infinita dei valori reciproci dei numeri di Fibonacci in posti dispari:
∑
n
=
1
∞
1
F
2
n
−
1
=
∑
n
=
1
∞
5
Φ
2
n
−
1
Φ
4
n
−
2
+
1
=
5
2
∑
n
=
1
∞
sech
(
(
n
−
1
2
)
arcosh
(
3
2
)
)
=
5
4
ϑ
10
(
Φ
−
2
)
2
=
5
π
λ
∗
(
16
π
−
2
ln
(
Φ
)
2
)
K
(
λ
∗
(
16
π
−
2
ln
(
Φ
)
2
)
)
.
{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{F_{2n-1}}}=\sum _{n=1}^{\infty }{\frac {{\sqrt {5}}\Phi ^{2n-1}}{\Phi ^{4n-2}+1}}={\frac {\sqrt {5}}{2}}\sum _{n=1}^{\infty }\operatorname {sech} {\big (}(n-{\tfrac {1}{2}})\operatorname {arcosh} ({\tfrac {3}{2}}){\big )}={\frac {\sqrt {5}}{4}}\vartheta _{10}(\Phi ^{-2})^{2}={\frac {\sqrt {5}}{\pi }}{\sqrt {\lambda ^{*}(16\pi ^{-2}\ln(\Phi )^{2})}}K{\big (}\lambda ^{*}(16\pi ^{-2}\ln(\Phi )^{2}){\big )}.}
Somma infinita dei valori reciproci dei quadrati dei numeri di Fibonacci:
∑
n
=
1
∞
1
F
n
2
=
5
12
ϑ
10
(
Φ
−
2
)
4
−
5
24
ϑ
00
(
Φ
−
2
)
4
+
5
24
.
{\displaystyle \sum _{n=1}^{\infty }{\frac {1}{F_{n}^{2}}}={\frac {5}{12}}\vartheta _{10}(\Phi ^{-2})^{4}-{\frac {5}{24}}\vartheta _{00}(\Phi ^{-2})^{4}+{\frac {5}{24}}.}




















![{\displaystyle \vartheta _{10}{\big (}\exp(-\pi {\sqrt {w}}){\big )}=\sum _{a=-\infty }^{\infty }\exp \left(-(a+{\tfrac {1}{2}})^{2}\pi {\sqrt {w}}\right)=\left(\sum _{a=-\infty }^{\infty }\operatorname {sech} \left((a+{\tfrac {1}{2}})\pi {\sqrt {w}}\right)\right)^{1/2}={\sqrt {2\pi ^{-1}\lambda ^{*}(w)K{\big (}\lambda ^{*}(w){\big )}}}=2{\sqrt[{4}]{\lambda ^{*}(4w)}}{\sqrt {\pi ^{-1}K{\big (}\lambda ^{*}(4w){\big )}}},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/bd0b67a7c50929d0fa193f29bdf574b4cd524897)








![{\displaystyle 2^{-5/4}3^{-3/8}{\sqrt {{\sqrt {3}}-1}}({\sqrt {3}}+1-{\sqrt[{4}]{12}}){\sqrt {G}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7f8eb52a4a7c3101c332febe36c212124176d8a8)
![{\displaystyle 2^{-5/4}3^{-3/8}{\sqrt {{\sqrt {3}}-1}}({\sqrt {3}}+1+{\sqrt[{4}]{12}}){\sqrt {G}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/af86cd23e633a604fde6d1eb0b9e4d7ecd1a8e02)

![{\displaystyle 2^{-1}({\sqrt[{4}]{2}}-1){\sqrt {G}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9544d5cd142396b876a166711921878944eeadc9)
![{\displaystyle 2^{-3/16}{\sqrt[{4}]{{\sqrt {2}}+1}}{\sqrt {G}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0f66de12836c895b0e74ff459ff31785955bcfb0)
![{\displaystyle 2^{-1}({\sqrt[{4}]{2}}+1){\sqrt {G}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/57c244679f3fc67d168f82f98e9c857f70c7868e)
![{\displaystyle 2^{-3/2}5^{-1/2}{\sqrt {{\sqrt {5}}-1}}({\sqrt[{4}]{5}}-1)^{2}{\sqrt {G}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/137b6868ad6a1c536b71d332ca05fb06b1d56d84)
![{\displaystyle 2^{-3/2}5^{-1/2}{\sqrt {{\sqrt {5}}-1}}({\sqrt[{4}]{5}}+1)^{2}{\sqrt {G}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/fbf38cde615814be0411a9fde934894f33a2528f)










