Momento angolare

Esempio di funzionamento del momento angolare

Il momento angolare (dal latino momentum: movimento, impulso o, in senso traslato, efficacia, influenza), o momento della quantità di moto, è una grandezza fisica di tipo vettoriale che rappresenta la quantità che si conserva se un sistema fisico è invariante sotto rotazioni spaziali. Costituisce l'equivalente per le rotazioni della quantità di moto per le traslazioni.

Più in generale, nelle formulazioni della meccanica discendenti da un principio variazionale il momento angolare è definito, in termini del teorema di Noether, come la quantità conservata risultante dall'invarianza dell'azione rispetto alle rotazioni tridimensionali. Questa formulazione è più adatta per estendere il concetto di momento angolare ad altri enti, quali ad esempio il campo elettromagnetico.

Il momento angolare è uno pseudovettore, non uno scalare come l'azione. Per questo motivo la sua unità di misura nel Sistema internazionale (SI) è espressa in $kg\cdot m^{2}\cdot s^{-1}$ (kilogrammo per metro quadro su secondo), non in joule per secondo, anche se le due unità hanno le stesse dimensioni fisiche. Una grandezza correlata al momento angolare è il momento angolare specifico $\mathbf {h}$ , il quale rappresenta il momento angolare per unità di massa, ovvero il momento della velocità.

Definizione

Momento angolare (${\vec {L}}$) di un punto materiale di massa $m$. Nell'immagine sono indicati il vettore posizione (${\vec {r}}$) e la velocità (${\vec {v}}$)

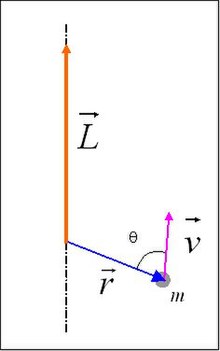
Nella meccanica newtoniana il momento angolare $\mathbf {L}$ rispetto ad un polo $O$ di un punto materiale è definito come il prodotto vettoriale tra il vettore che esprime la posizione $\mathbf {r}$ del punto rispetto a $O$ e il vettore quantità di moto $\mathbf {p}$:

$\mathbf {L} _{O}=\mathbf {r} \times \mathbf {p} =\mathbf {r} \times m\mathbf {v}$

Il modulo di $\mathbf {L} _{O}$ è quindi definito da:

$\|\mathbf {L} _{O}\|=\|\mathbf {r} \|\cdot \|\mathbf {p} \|\sin {\theta }=\mathbf {p} \cdot \mathbf {b} =m\mathbf {v} \cdot \mathbf {b}$

La direzione di $\mathbf {L} _{O}$ è perpendicolare al piano definito da $\mathbf {p}$ e da $\mathbf {r}$ e il verso è quello di un osservatore che vede ruotare $\mathbf {p}$ in senso antiorario. Il vettore $\mathbf {b} =\mathbf {r} \sin {\theta }$, che rappresenta la distanza dell'asse di rotazione dalla retta su cui giace $\mathbf {p}$, è detto braccio di $\mathbf {p}$.

Se $\mathbf {p}$ e $\mathbf {r}$ sono tra loro perpendicolari, si ha che $\sin \theta =1$, pertanto il momento angolare è massimo. Il momento angolare è nullo invece se la quantità di moto o il braccio sono nulli, oppure se $\mathbf {p}$ è parallelo ad $\mathbf {r}$, in tal caso infatti $\sin \theta =0$.

Poiché il prodotto di due variabili coniugate, ad esempio posizione e impulso, deve essere un'azione, questo ci dice che la variabile coniugata al momento angolare deve essere adimensionale: infatti è l'angolo di rotazione attorno al polo.

Momento angolare assiale

Si definisce momento angolare assiale rispetto a un asse ${\hat {z}}$ passante per un punto $O$ la componente ortogonale del momento angolare su un particolare asse ${\hat {z}}$, detto asse centrale:

$\mathbf {L} _{\hat {z}}:=[(\mathbf {r} \times \mathbf {p} )\cdot {\hat {\mathbf {z} }}]{\hat {\mathbf {n} }}$

dove ${\hat {\mathbf {n} }}$ è un versore, vettore di lunghezza unitaria, che identifica l'asse. Il modulo sarà:

$L_{\hat {n}}=|\mathbf {L} _{O}|\cdot \cos \varphi =|\mathbf {r} |\cdot |\mathbf {p} |\sin \vartheta \cos \varphi =(\mathbf {p} \cdot \mathbf {b} )\cos \varphi$

dove $\varphi$ è l'angolo formato dal vettore momento angolare $\mathbf {L} _{O}$ con l'asse ${\hat {n}}$. In pratica è la proiezione ortogonale del momento angolare sull'asse ${\hat {n}}$. Per questo il momento angolare assiale è nullo se l'angolo $\varphi =\pi /2$ e massimo quando l'asse ${\hat {z}}$ coincide con l'asse di $\mathbf {L} _{O}$, in tal caso infatti: $\varphi =0$.

Momento angolare per sistemi di punti materiali

Per sistemi discreti il momento angolare totale è definito dalla somma dei singoli momenti angolari:

$\mathbf {L} =\sum _{i}\mathbf {L} _{i}=\sum _{i}m_{i}\mathbf {r} _{i}\times \mathbf {v} _{i}$

dove $\mathbf {r} _{i}$ è il vettore posizione del punto i-esimo rispetto all'origine, $m_{i}$ è la sua massa, e $\mathbf {v} _{i}$ è la sua velocità. Sapendo che la massa totale di tutte le particelle è data da:

$m=\sum _{i}m_{i}$

si ha che il centro di massa è definito da:

$\mathbf {r} _{\text{CM}}={\frac {1}{m}}\sum _{i}m_{i}\mathbf {r} _{i}$

ne consegue che la velocità lineare del centro di massa è:

$\mathbf {v} _{\text{CM}}={\frac {1}{m}}\sum _{i}m_{i}\mathbf {v} _{i}.\,$

Se si definiscono $\mathbf {r} '_{i}$ il vettore posizione della particella , e $\mathbf {v} '_{i}$ la sua velocità rispetto al centro di massa, si ha:

$\mathbf {r} _{i}=\mathbf {r} _{\text{CM}}+\mathbf {r} '_{i}$ e $\mathbf {v} _{i}=\mathbf {v} _{\text{CM}}+\mathbf {v} '_{i}$

si può vedere che:

$\sum _{i}m_{i}\mathbf {r} '_{i}=0$   e    $\sum _{i}m_{i}\mathbf {v} '_{i}=0$

cosicché il momento angolare totale rispetto all'origine è:

$\mathbf {L} =\sum _{i}\mathbf {r} _{i}\times m_{i}\mathbf {v} _{i}=\left(\mathbf {r} _{\text{CM}}\times m\mathbf {v} _{\text{CM}}\right)+\sum _{i}(\mathbf {r} '_{i}\times m_{i}\mathbf {v} '_{i})=\mathbf {L} _{CM}+\mathbf {L} '_{i}$

Il primo termine è semplicemente il momento angolare del centro di massa. È il medesimo momento angolare che si otterrebbe se ci fosse una sola particella di massa $m$, posta nel centro di massa, che si muove con velocità $\mathbf {v}$. Il secondo termine è il momento angolare delle particelle relativamente al proprio centro di massa. Nei sistemi continui si estende in modo naturale la definizione introducendo la densità $\rho$ e il campo di velocità $\mathbf {v} (\mathbf {r} )$:

$\mathbf {L} =\int _{V}\rho \,\mathbf {r} \times \mathbf {v} \ \mathrm {d} V$

Legame con il moto rotatorio

Se le particelle formano un corpo rigido, il termine che descrive il loro momento angolare rispetto al centro di massa può essere ulteriormente semplificato. In questo caso, infatti, è possibile legare la sua espressione alla descrizione del moto rotatorio, ovvero alla velocità angolare ${\boldsymbol {\omega }}$ e alla velocità areolare ${\dot {\mathbf {A} }}$. Se la componente rotatoria è l'unica presente, ovvero nel caso in cui il corpo rigido si muova di moto circolare, è pari al prodotto del tensore di inerzia ${\underline {\underline {\mathbf {I} }}}$ e della velocità angolare:

$\mathbf {L} ={\underline {\underline {\mathbf {I} }}}{\boldsymbol {\omega }}$

oppure, analogamente, come il doppio del prodotto tra la massa totale e la velocità areolare:

$\mathbf {L} =2m{\dot {\mathbf {A} }}$

Lo stesso risultato si ottiene se al sistema di punti materiali discreti esaminato sopra si sostituisce una distribuzione continua di massa.

Legame con il momento meccanico

Relazione tra forza ($\mathbf {F}$), momento meccanico (${\boldsymbol {\tau }}$), quantità di moto ($\mathbf {p}$) e momento angolare ($\mathbf {L}$) in un sistema rotante.

Per quanto riguarda la dinamica dei sistemi di punti materiali, il momento angolare è una caratteristica fondamentale del moto. Infatti se un punto materiale $P$ si muove con quantità di moto: $\mathbf {p} =m\mathbf {v}$, il momento angolare del punto rispetto a un polo $O$ è dato da:

$\mathbf {L} =\mathbf {r} (t)\times \mathbf {p} (t)$

se il polo $O$ è in moto con velocità $\mathbf {v} _{O}$, allora il momento angolare varia nel tempo:

${\frac {\mathrm {d} \mathbf {L} }{\mathrm {d} t}}={\frac {\mathrm {d} }{\mathrm {d} t}}\left(\mathbf {r} \times \mathbf {p} \right)={\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}\times \mathbf {p} +\mathbf {r} \times {\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}$

dove:

• ${\frac {\mathrm {d} \mathbf {r} }{\mathrm {d} t}}$ rappresenta la velocità relativa del punto $P$ rispetto alla velocità di $O$
• ${\frac {\mathrm {d} \mathbf {p} }{\mathrm {d} t}}$ per il secondo principio della dinamica rappresenta la forza totale risultante.

Allora da questa relazione si ricava la seconda equazione cardinale della dinamica:

${\frac {\mathrm {d} \mathbf {L} }{\mathrm {d} t}}=(\mathbf {v} -\mathbf {v} _{O})\times \mathbf {p} +\mathbf {r} \times \mathbf {F} =\mathbf {v} \times \mathbf {p} -\mathbf {v} _{O}\times \mathbf {p} +\mathbf {M} _{O}$

essendo $\mathbf {v}$ e $\mathbf {p}$ paralleli, il loro prodotto vettoriale è nullo, dunque si ottiene:

$\mathbf {M} _{O}={\frac {\mathrm {d} \mathbf {L} }{\mathrm {d} t}}+\mathbf {v} _{O}\times \mathbf {p}$

dove $\mathbf {M} _{O}=\mathbf {r} \times \mathbf {F}$ è il momento meccanico. Nel caso di un corpo rigido rotante, si può osservare che $\mathbf {v} _{O}$ rappresenta la velocità tangenziale del corpo rotante, pertanto si ha che:

${\frac {\mathrm {d} \mathbf {L} }{\mathrm {d} t}}=\mathbf {M} -\mathbf {v} _{O}\times \mathbf {p} =\mathbf {M} -{\boldsymbol {\omega }}\times \mathbf {r} \times \mathbf {p} =\mathbf {M} -{\boldsymbol {\omega }}\times \mathbf {L}$

Nei casi in cui:

• il polo sia fermo
• il polo coincida con il centro di massa
• il polo si muova parallelamente alla traiettoria del centro di massa

allora ci si riconduce alla più familiare:

$\mathbf {M} ={\frac {\mathrm {d} \mathbf {L} }{\mathrm {d} t}}$

Il momento di una forza è definito come il prodotto vettoriale tra il vettore posizione del punto di applicazione della forza, e la forza stessa. Il suo modulo risulta quindi uguale al modulo della forza per il braccio. Si può dimostrare che se il polo è immobile, la derivata rispetto al tempo del momento angolare è uguale al momento delle forze applicate, cosicché se quest'ultimo momento è nullo allora il momento angolare si conserva.

Conservazione del momento angolare ed esempi

Il momento angolare è importante in tutti i moti dipendenti da variazioni che riguardano variabili angolari, inoltre resta fondamentale perché nei sistemi isolati, cioè non soggetti a momenti di forze esterne, vale la legge di conservazione del momento angolare.

Impulso angolare

Viene definito impulso angolare la variazione del momento angolare di un corpo che viene sottoposto ad un urto con un altro corpo. In altre parole è il momento angolare effettivamente trasmesso al momento dell'urto. Il momento angolare iniziale e finale, utili per calcolare l'impulso angolare, consistono nei momenti della quantità di moto finale e della quantità di moto iniziale. Dunque per calcolare l'impulso angolare in genere si usa misurare massa e velocità del corpo prima del contatto e trarre i dati iniziali e ripetere l'operazione dopo il contatto. Sfruttando la seconda equazione cardinale della dinamica di Eulero e la legge della cinematica di un moto circolare uniforme si ha che:

$\mathbf {M} ={\frac {\mathrm {d} \mathbf {L} }{\mathrm {d} t}}$

Integrando rispetto al tempo entrambi i membri si ottiene l'impulso angolare:

$\Delta \mathbf {L} =\int _{t_{1}}^{t_{2}}\mathbf {M} \,\mathrm {d} t$

Forze centrali

Nello studio dei moti in campi di forze centrali, la conservazione del momento angolare è fondamentale, poiché è legata alla costanza della velocità areolare. Esempi di questo tipo si riscontrano in meccanica newtoniana, ad esempio nello studio del moto del pendolo, e in meccanica celeste, dove il momento angolare orbitale, definito come il prodotto vettoriale tra la posizione e la quantità di moto del corpo orbitante al tempo di riferimento, riveste un ruolo chiave per le leggi di Keplero e lo studio dei moti dei pianeti, infatti il momento angolare orbitale specifico rappresenta una costante vettoriale di moto di un'orbita, cioè si conserva nel tempo.

Bibliografia

• Sergio Rosati, Fisica Generale, Milano, Casa Editrice Ambrosiana, 1990, ISBN 88-408-0368-8.
• Paolo Mazzoldi, Massimo Nigro, Cesare Voci, Fisica - Volume I (seconda edizione), Napoli, EdiSES, 2010, ISBN 88-7959-137-1.
• Gian Paolo Parodi, Marco Ostili, Guglielmo Mochi Onori, L'Evoluzione della Fisica-Volume 1, Paravia, 2006, ISBN 978-88-395-1609-1.
• David Halliday, Robert Resnick, Fundamentals of Physics, John Wiley & Sons, 1960-2007, pp. Chapter 10.

Voci correlate

• Momento meccanico
• Operatore momento angolare
• Momento angolare specifico
• Primo teorema di König

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file sul momento angolare

Collegamenti esterni

• (EN) angular momentum, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
• Momento angolare su Treccani.it, novembre 2013