Modello di Sommerfeld
In fisica dello stato solido il modello di Sommerfeld detto anche modello dell'elettrone libero è un semplice modello quantistico che descrivere il comportamento dei portatori di carica nei solidi metallici. Tale modello è stato sviluppato da Arnold Sommerfeld che ha combinato il modello di Drude (un modello che considera gli elettroni come un gas ideale classico, non riuscendo tuttavia a giustificare da solo la conducibilità elettrica dei metalli al variare della temperatura) con la statistica quantistica di Fermi-Dirac.
Il modello è molto semplice, ma riesce a dare una soddisfacente spiegazione di molti fatti sperimentali:
- conduttività elettrica;
- legge di Wiedemann-Franz che mette in relazione la conducibilità termica alla conduttività elettrica;
- dipendenza dalla temperatura del calore specifico elettronico;
- dipendenza approssimativa dall'energia della densità degli stati;
- compressibilità dei metalli;
- cammino libero medio
- Effetto Seebeck
Il miglioramento diretto di questo modello si ha con la teoria delle bande.
Per non appesantire il testo molti ragionamenti non sono esplicitati in quanto si rimanda al modello di Drude per lo sviluppo completo, infatti la differenza con tale modello è solo da un punto di vista statistico.
Ipotesi[modifica | modifica wikitesto]
Gli elettroni di valenza sono considerati completamente liberi e costituiscono a tutti gli effetti un gas ideale di elettroni. Come nel caso di un gas ideale la interazione elettrone-elettrone è completamente trascurata.
La struttura cristallina non è tenuta in considerazione. L'unico limite del modello è dato dalla scatola cubica di lato in cui sono contenuti gli elettroni.
La statistica a cui obbedisce tale gas quantistico è la statistica di Fermi-Dirac[1].
Modello stazionario[modifica | modifica wikitesto]
Consideriamo una scatola cubica di lato dentro cui sono contenute elettroni non interagenti. Si può dimostrare che la forma della scatola modifica i risultati finali in maniera irrilevante. Immaginiamo che il potenziale sia infinito all'esterno della scatola, di conseguenza la funzione d'onda deve essere nulla all'esterno della scatola stessa. Se scegliamo l'origine delle coordinate coincidente con un vertice del cubo e gli assi cartesiani orientati come i suoi spigoli, la funzione d'onda soddisferà per ragioni di continuità le equazioni:
La soluzione del problema è la combinazione lineare di onde piane viaggianti in direzioni opposte:
Tale equazione può essere riscritta come:
La necessità che vengano soddisfatte le condizioni al contorno richiede che le componenti di devono assumere solo dei valori discreti:

Dove , ed devono essere numeri positivi ed interi. Non sono soluzioni possibili nemmeno quelle soluzioni per cui uno solo degli è nullo: verrebbe infatti violato il principio di indeterminazione in quella direzione.
Se noi disegniamo, nello spazio , l'insieme dei punti che sono soluzioni del problema di particelle nella scatola cubica di lato , otteniamo un reticolo cubico semplice di punti in un solo ottante di tale spazio.
Allo zero assoluto mi aspetto che siano occupati solo gli stati con minore energia rispettando il principio di esclusione di Pauli. Il numero di elettroni nei solidi macroscopici è molto elevato per cui se andiamo a disporre i nostri elettroni negli stati possibili riempiendo prima gli stati con basso (bassa energia) e poi via via quelli con più elevato (grande energia). Dato che il numero è molto elevato si può trascurare la discretizzazione degli stati. Nello spazio gli stati possibili occupano i punti di un reticolo cubico semplice. La distanza tra punti adiacenti di tale reticolo vale ovviamente: . Nei reticoli cubici semplici di parametro reticolare , la densità dei punti reticolari vale ovviamente . Abbiamo che la densità dei punti nello spazio vale:
dove è il volume del cubo. Abbiamo calcolato tale densità di punti, ma ogni stato può essere occupato da due soli elettroni a causa del principio di esclusioni di Pauli, avendo gli elettroni un ulteriore grado di libertà interno dovuto allo spin semintero. Quindi per ogni stato permesso alla funzione d'onda di un elettrone, ci sono due stati elettronici, che corrispondono alle due possibili direzioni verso cui può puntare il momento angolare di un elettrone.
Quindi la densità di stati elettronici nello spazio vale:
Il significato fisico di (estendendo la sua definizione dallo spazio discreto a quello continuo) è che vi sono nel volume dello spazio un numero elettroni.
Possiamo determinare il raggio dell'ottavo di sfera contenente gli elettroni del metallo:
Si noti come si faccia un errore, trascurabile, dovuto all'inclusione dei punti sui tre piani cartesiani. Dalla equazione si ricava che:
Il raggio del settore sferico viene detto vettore d'onda di Fermi. Al contrario del caso classico quindi gli elettroni in un metallo anche a temperatura bassissima hanno un vasto range di valori di vettori d'onda e di conseguenza di energie cinetiche fino ad un certo valore massimo dipendente soltanto dalla densità degli elettroni.
Condizione al contorno periodica[modifica | modifica wikitesto]
La condizione data sulla funzione d'onda, che imponeva il suo annullarsi sulla superficie del cubo, è nella pratica poco soddisfacente, infatti porta come conseguenza che le soluzioni del problema siano onde stazionarie. Nei solidi macroscopici l'interazione degli elettroni con gli estremi del solido è spesso trascurabile nei fenomeni di trasporto di energia e carica: soluzioni quindi propagantesi descrivono meglio i fenomeni fisici di interesse, tranne che per i al limite della I zona di Brillouin, ma nel modello la periodicità del reticolo è trascurata. Le proprietà generali di un solido macroscopico ( è possibile dimostrarlo in maniera rigorosa[2] ) non dipendono dalle condizioni al contorno.

Una scelta più soddisfacente delle condizioni al contorno è quella di una condizione al contorno periodica, detta anche condizione al contorno di Born-Von Karman: si immagina che ogni faccia del cubo sia unita alla superficie opposta, in maniera tale che ogni elettrone che arrivi su una superficie non sia riflesso dalla superficie stessa, ma lasci il metallo entrando di nuovo dalla faccia opposta. Una condizione di tale tipo impone che la densità degli elettroni non vari lungo il solido. In tali termini la condizione sulla funzione d'onda è del tipo:
Le soluzioni del problema sono in tale caso semplicemente delle onde piane:
La necessità che vengano soddisfatte le condizioni al contorno richiede che le componenti di possano assumere solo dei valori discreti:
Dove , ed devono essere numeri interi positivi o negativi, ma non tutti nulli. Nello spazio k tali punti costituiscono un reticolo cubico. La distanza tra i punti del reticolo cubico semplice degli stati permessi, è due volte più grande rispetto alla precedente condizione al contorno. Quindi nello spazio l'insieme dei punti che sono soluzioni del problema di particelle nella scatola periodica di lato è un reticolo cubico semplice di punti di tale spazio, ma disposti simmetricamente intorno agli assi delle coordinate. Ma la distanza tra i punti del reticolo nello spazio normalmente provoca nessun effetto misurabile nei solidi macroscopici.
Tale condizioni portano alle stessa soluzione per quanto riguarda . Infatti ripetendo i ragionamenti nel caso .
Gli elettroni andranno quindi a riempire una sfera di raggio (non più un ottavo di sfera):
che è la stessa equazione di quella ricavata precedentemente. Quindi il vettore d'onda di Fermi è identico con tale condizione al contorno. La regione nello spazio permessa agli stati di un elettrone è una sfera.
Energia di Fermi[modifica | modifica wikitesto]
Poiché gli elettroni sono liberi la relazione di dispersione tra e vale:
quindi al valore massimo per corrisponde una energia massima, detta energia di Fermi:
o se si vuole una velocità quadratica massima
Si definisce temperatura di Fermi:
La velocità di Fermi ha un valore simile per tutti i metalli ed è circa della velocità della luce. L'esistenza di questa velocità spiega la ragione per cui i segnali elettrici nei metalli si propagano con la stessa velocità, circa la velocità di Fermi, indipendentemente dalla temperatura. La velocità di Fermi gioca nella teoria dei metalli un ruolo analogo alla velocità quadratica media termica di un gas classico.
Il modulo del vettore d'onda di Fermi ha un valore paragonabile a quello della prima zona di Brillouin. La sfera di raggio , contenente i livelli occupati una volta sola è detta sfera di Fermi. La superficie della sfera di Fermi che separa gli stati occupati da quelli non occupati si chiama superficie di Fermi.
| Elemento | |||
|---|---|---|---|
| Na | 3.24 | 40 | 1.1 |
| Cu | 7 | 82 | 1.6 |
| Al | 12 | 136 | 2.0 |
| Fe | 11 | 130 | 2.0 |
Densità degli stati[modifica | modifica wikitesto]
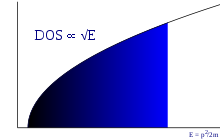
La densità degli stati, ovvero il numero di stati per unità di volume con vettore d'onda minore o uguale a vale:
Ma essendo posso scrivere l'equazione precedente in funzione di :
Ma se definiamo la densità degli stati per unità di volume con energia compresa tra ed è legata al numero di stati per unità di volume:
Da cui:
spesso si preferisce eliminare la massa degli elettroni dall'espressione e riscrivere l'espressione come:
Il potenziale chimico e la temperatura[modifica | modifica wikitesto]
Qui proviamo ad estendere quanto detto al caso di temperatura diverso da zero. Infatti la densità degli stati, in prima approssimazione, non cambia con la temperatura come pure il numero degli stati.
A temperatura abbiamo supposto che tutti gli elettroni stavano in livelli con energia minore od eguale ad . Se aumentiamo la temperatura, alcuni degli elettroni vicino alla superficie di Fermi potranno andare al di fuori della superficie di Fermi. Quindi a la probabilità di occupazione dello stato energetico diventa non più :
come abbiamo supposto per , ma assume una forma diversa che tiene conto del principio di esclusione di Pauli
Tendendo conto di tale principio si dimostra che per i fermioni la probabilità di occupazione dello stato con energia vale:
Dove , che ha le dimensioni di una energia, si chiama potenziale chimico e rappresenta l'energia da fornire al sistema per aggiungere un fermione, o se si vuole quando la probabilità di occupazione diventa . Tale distribuzione della probabilità viene detta distribuzione di Fermi-Dirac. Qualsiasi fluido di fermioni ha una distribuzione delle energie che segue tale distribuzione.
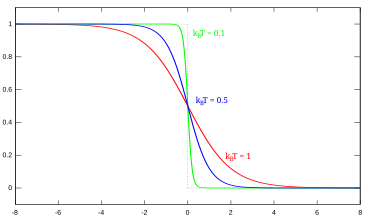
Facilmente si può verificare come per la distribuzione di Fermi-Dirac vale:
Quindi il potenziale chimico coincide con l'energia di Fermi per :
A una temperatura qualsiasi la densità di elettroni con energia compresa tra ed diviene uguale a:
L'integrale di per deve essere la densità totale di elettroni liberi del metallo:
Imponendo che sia indipendente dalla temperatura (come è ovvio) segue, mediante dei passaggi matematici qua non esplicitati[3], che:
Quindi a temperatura ambiente il potenziale chimico si discosta dall'energia di Fermi in maniera non significativa per tutti i metalli. Spesso per questa ragione si confonde il concetto di potenziale chimico con l'energia di Fermi.
Calore specifico elettronico[modifica | modifica wikitesto]
L'energia totale del gas di elettroni in funzione della temperatura è pari a:
dove è il volume del metallo. Sviluppando in serie di Taylor la distribuzione di Fermi-Dirac attorno all'energia di Fermi, si trova che:
Dove è l'energia nello stato fondamentale, quindi il calore specifico vale:
Notiamo come in tale espressione si sia volutamente non esplicitato , in quanto il conto è valido non solo nel caso del modello degli elettroni liberi: vale qualunque sia la funzione densità degli stati.
Nel caso che il modello dell'elettrone libero sia applicabile sostituendo a la sua espressione esplicita, si ricava:
Tra parentesi è stato messo in evidenza il termine che si era ricavato nella ipotesi che il gas di elettroni fosse classico (modello di Drude). Quindi l'effetto della statistica di Fermi-Dirac è di diminuire il valore previsto del calore specifico di , che vuol dire a temperatura ambiente un fattore dell'ordine di 100. Questo risultato è in buon accordo con quanto si trova sperimentalmente a temperatura ambiente, cioè che nei solidi non vi è differenza tra conduttori e non conduttori per quanto riguarda il calore specifico. Se, infatti, il gas di elettroni fosse una gas classico ci aspetteremmo un importante contributo al calore specifico dovuto agli elettroni di conduzione.
A bassa temperatura il contributo al calore specifico dovuto ai fononi, modello di Debye, scende con la temperatura con un andamento del tipo , per cui al di sotto di certe temperature il contributo del calore specifico dovuto agli elettroni di conduzione diventa il termine più rilevante; il calore specifico totale dei metalli, a temperature più basse di quella di Debye, ha una espressione del tipo:
con . Sperimentalmente in tutti i metalli il calore specifico dovuto agli elettroni, a bassa temperatura, segue una legge lineare con la temperatura. La costante moltiplicativa è in buon accordo con il valore appena dato solo per i metalli alcalini, negli altri metalli si trova una costante moltiplicativa diversa da quella prevista dal modello di Sommerfield. La teoria a bande rimuove tale incongruenza dovuta alla semplicità del modello.
Conducibilità elettrica[modifica | modifica wikitesto]
Esaminiamo la conducibilità elettrica usando il modello dell'elettrone libero della meccanica quantistica. A temperatura nulla gli elettroni occupano degli stati all'interno della sfera di Fermi nello spazio . Essendo la sfera di Fermi centrata attorno a per ogni stato con un certo valore ne esisterà un altro in maniera tale che la quantità di moto totale del gas di elettroni è nulla.
La cosa non cambia a infatti la distribuzione di Fermi-Dirac rende semplicemente meno netta la occupazione degli stati nella zona vicina alla sfera di Fermi, ma ugualmente vi è un'esatta compensazione dei vettori d'onda. Infatti la distribuzione degli stati non cambia con la temperatura.
L'applicazione di un campo elettrico cambia l'equazione di Schrödinger con l'aggiunta di un termine costante additivo in assenza di dissipazione. Ma se, con considerazioni simili a quelle che si vengono fatte nel caso classico, modello di Drude, si tiene conto della interazione con le imperfezioni l'effetto medio del campo elettrico è solo un aumento alle velocità possedute da ogni elettrone di una velocità di drift . Quindi il vettore d'onda di ogni elettrone cambierà di:
Quindi tutti gli elettroni si muovono nei nuovi stati spostati di dai vecchi. Gli stati occupati stanno ancora in una sfera, ma ora tale sfera è centrata attorno a .
Notiamo che è in direzione opposta ad a causa della carica negativa degli elettroni. Vediamo come ora non tutti gli elettroni sono in coppie di e . Alcuni stati su una sfera non sono occupati come prima ed altri sulla direzione opposta, che non erano occupati, sono ora occupati. C'è quindi uno sbilanciamento ed il valore medio della quantità di moto totale non è più nullo, quindi si ha una corrente elettrica.
Essendo , l'effetto è piccolo e quasi tutti gli elettroni sono compensati a coppie. Gli elettroni non compensati sono solo in una piccolissima regione attorno alla superficie di Fermi. Tutti gli altri elettroni sono compensati e loro quantità di moto media è nulla. Tali elettroni non contribuiscono assolutamente alla corrente elettrica. La corrente elettrica dipende solamente dagli elettroni non compensati vicini alla superficie di Fermi. Quindi sono una piccolissima frazione degli elettroni partecipano alla conduzione. Quindi a differenza dal caso classico dove tutti gli elettroni partecipavano alla conduzione con una velocità media , nel quadro quantistico solo gli elettroni con velocità circa eguale a quella di Fermi partecipano alla conduzione. Quindi il numero di tali elettroni è circa:
quindi la densità di corrente sarà circa:
che è lo stesso valore trovato nel caso classico, ma con un numero estremamente ridotto di elettroni di conduzione.
Nel modello quantistico, ha le dimensioni di una velocità, ma è legato allo spostamento della superficie di Fermi, e non la media velocità di drift come nel modello di Drude.
Utilizzando gli stessi ragionamenti del modello di Drude si ricava che:
ora è il tempo medio tra una collisione e la successiva per gli elettroni vicini la superficie di Fermi.
La conducibilità elettrica quindi diventa eguale a:
Quindi, poiché la forma della distribuzione delle velocità degli elettroni non influenza il calcolo della conducibilità in DC ed in AC o nel calcolo del coefficiente di Hall, la trattazione di questi fenomeni non cambia sostanzialmente se si usa la statistica classica o quella di Fermi-Dirac.
Il cammino libero medio è:
e rappresenta la distanza media percorsa dai soli elettroni vicino alla superficie di Fermi. Il modello di Drude considera il cammino libero medio connesso alla distanza tra gli ioni nel materiale, questo implica un moto diffusivo degli elettroni dovuto alla collisione con gli ioni. Nel modello di Sommerfield il cammino libero medio dipende dalla velocità di Fermi e quindi è un ordine di grandezza maggiore del caso classico, come si anche viene verificato sperimentalmente. Il cammino libero è quindi non il risultato della collisione con gli ioni, ma invece è legato alle imperfezioni dei materiali, i difetti e alle fluttuazioni termiche<[4].
Conducibilità termica[modifica | modifica wikitesto]
Uno dei grandi successi del modello di Drude è il buon accordo con il risultato sperimentale della conducibilità termica: i metalli buoni conduttori di elettricità sono buoni conduttori di calore. In realtà l'accordo è dovuto a un doppio errore nella formula utilizzata, in ogni caso il risultato del modello di Drude è errato per un fattore due. Possiamo, facendo un ragionamento simile a quanto fatto nel modello di Drude, ricavare che la costante che compare nella legge di Fourier è data da:
A differenza del modello di Drude, in cui vale la stessa espressione, le grandezze fisiche che compaiono hanno un valore diverso e sono: la velocità di Fermi ,il tempo di collisione di Fermi e il calore specifico dal gas quantistico di elettroni , quindi:
Questa costante detta di Lorentz è molto simile al valore sperimentale della maggior parte dei metalli ed è esattamente il valore previsto dalla legge empirica di Wiedemann-Franz. Il valore previsto della costante di Lorentz dal modello di Drude è invece due volte più piccolo.
Compressibilità dei metalli[modifica | modifica wikitesto]
L'energia totale per unità di volume a seguendo questo modello è pari a:
Notiamo che non dipende dalla temperatura al contrario di quanto si trova con il modello di Drude in cui l'energia di ogni singolo elettrone vale , che si annulla a temperatura zero. Quindi per avere la stessa energia il gas di elettroni classio dovrebbe trovarsi a circa la temperatura di Fermi. Possiamo calcolare la pressione allo zero assoluto:
dove è il volume and è la energia totale, la derivta è fatta a temperatura e potenziale chimico costante. Questa pressione è detta pressione di degenerazione degli elettroni e deriva dal principio di esclusione di Pauli. Questa pressione permette di calcolare il modulo di compressibilità del metallo:
Con questa espressione si ottiene l'ordine di grandezza giusto del modulo di compressibilità dei metalli alcalini e dei metalli nobili. In genere negli altri metalli vi è una discrepanza maggiore dovuta al fatto che in questo ragionamento non si è tenuto conto della struttura cristallina che chiaramente ha un ruolo.
Effetto Seebeck[modifica | modifica wikitesto]
L'effetto Seebeck è un effetto termoelettrico, che si ha quando vi è una differenza di temperatura tra due parti di un metallo. Il gas di elettroni, come un gas di particelle sarà più diradato nella regione più calda, e quindi ci aspetta che, essendo gli elettroni carichi, si generi una differenza di potenziale. La costante di Seebeck, cioè la costante di proporzionalità tra differenza di temperatura e differenza di potenziale, con un ragionamento simile al modello di Drude, può riscriversi come:
sostituendo a si ha che:
Si è lasciato in parentesi il termine previsto dal modello di Drude, in questo caso il modello di Drude prevede erroneamente una costante di Seebeck di un paio di ordini di grandezza maggiore di quanto trovato sperimentalmente e mentre il modello di Sommerfeld prevede il giusto ordine di grandezza.
Note[modifica | modifica wikitesto]
- ^ N.W. Ashcroft and N.D. Mermin "Solid State Physics", 1976, pp 30-53, ISBN 978-0-03-083993-1
- ^ J. L. Lebowitz e E. H. Lieb, Phys. Rev. Lett. 1969; 22 631.
- ^ N.W. Ashcroft and N.D. Mermin "Solid State Physics", 1976, pp 41-47, ISBN 978-0-03-083993-1
- ^ Evgeny Tsymbal, Electronic Transport (PDF), su University of Nebraska-Lincoln, 2008.
Voci correlate[modifica | modifica wikitesto]
- Modello di Drude
- Struttura elettronica a bande
- Calore specifico
- Conduttività elettrica
- Conducibilità termica
- Modulo di compressibilità
- Legge di Wiedemann-Franz
- Effetto Seebeck
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) free electron / free-electron model of metals, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.





![{\displaystyle \psi (x,y,z)=A\left[e^{i{\vec {k}}\cdot {\vec {r}}}-e^{-i{\vec {k}}\cdot {\vec {r}}}\right]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/2adf6f08aa9b992d12fa7156d9f76f6eebae3c55)














































































![{\displaystyle \mu =E_{F}\left[1-{\frac {1}{3}}\left({\frac {\pi k_{B}T}{2E_{F}}}\right)^{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d71d87d70236c978f2fdec22bf678e1384fc127)













































