Teorema di Modigliani-Miller
In finanza, il teorema di Modigliani-Miller (dagli economisti Franco Modigliani e Merton Miller che ne proposero la formulazione originale) costituisce la base della moderna teoria della struttura del capitale. Nella sua formulazione più semplice, il teorema afferma che, in assenza di tasse, costi di fallimento, asimmetrie informative, in un mercato efficiente il valore di un'impresa non è affetto dalla modalità con cui l'impresa si finanzia. Non importa dunque se l'impresa ottiene il proprio capitale raccogliendo finanziamenti tramite l'emissione di azioni o tramite debito; allo stesso modo la politica di dividendo non ha effetti sul valore dell'impresa. Il teorema è costituito da due proposizioni distinte, che possono essere estese a una situazione che prevede la presenza di tassazione.
Il teorema di Modigliani-Miller rappresenta inoltre un importante contributo alla teoria della finanza aziendale, o corporate finance, dal punto di vista metodologico; con il lavoro di Modigliani e Miller del 1958 si introducono infatti per la prima volta gli strumenti analitici formali dell'economia politica nell'analisi di un problema di finanza aziendale .
Proposizioni del teorema di Modigliani-Miller[modifica | modifica wikitesto]
Si considerino due imprese, identiche in tutto salvo la struttura del capitale. La prima impresa, detta U, è unlevered, ossia il suo capitale è interamente costituito da capitale di rischio (cioè è interamente versato dagli azionisti nel caso di una società per azioni). L'altra impresa, detta L, è levered, ossia il suo capitale è in parte costituito da equity o capitale di rischio, in parte da debito. La prima proposizione del teorema di Modigliani-Miller afferma che il valore delle due imprese è il medesimo:
dove è il valore dell'impresa U, quello dell'impresa L. è pari al costo di acquistare tutte le azioni dell'impresa U, al costo di acquistare tutte le azioni dell'impresa L e di ripagarne il debito per intero.
Il ragionamento alla base del risultato è brevemente illustrato: si consideri il caso di un investitore che intende acquistare l'impresa U o l'impresa L. Invece di acquistare tutte le azioni dell'impresa U, potrebbe acquistare le azioni dell'impresa L e indebitarsi per un ammontare pari al debito di L. I rendimenti da entrambi gli investimenti sarebbero identici. Dunque il valore di tutte le azioni di L (o equity di L) deve essere uguale a quello di tutte le azioni di U, meno il debito di L.
Questa discussione chiarifica alcune delle ipotesi del teorema. Si è infatti implicitamente ipotizzato che il costo del debito per l'investitore sia lo stesso che per l'impresa L; ciò non è necessariamente verificato in caso di mercati inefficienti o asimmetrie informative.
Quanto alla seconda proposizione, essa stabilisce la seguente relazione tra costo del capitale dell'equity, o capitale di rischio, , per un'impresa indebitata, il costo del capitale per un'impresa il cui capitale è costituito esclusivamente da equity, , il costo del debito e il rapporto debito-equity (o leva finanziaria, a seconda delle definizioni) :
La proposizione afferma dunque che il costo del capitale dell'equity è una funzione lineare della leva finanziaria dell'impresa. Una maggiore leva finanziaria (ovvero più debito rispetto al capitale) implica un più alto costo del capitale proprio, a causa del maggiore rischio (ad es., di insolvenza) a carico degli azionisti dell'impresa.
Entrambe le proposizioni sono valide sotto l'ipotesi che non sussistano imposizione fiscale e costi di transazione, nonché che investitori e imprese possano indebitarsi allo stesso tasso. Se da un lato queste condizioni non sono in genere verificate nei mercati reali, come fatto rilevare dagli stessi Modigliani e Miller nel loro contributo originale, l'importanza del teorema sta nel fatto che la struttura del capitale ha rilevanza precisamente perché una delle condizioni è violata. Il teorema fornisce dunque delle indicazioni circa quali fattori possano determinare la struttura del capitale.
Estensioni[modifica | modifica wikitesto]
Risultato di Modigliani-Miller in presenza di tassazione[modifica | modifica wikitesto]
In presenza di tassazione, le espressioni presentate sopra sono leggermente modificate. Denotando tramite l'aliquota d'imposta e tramite il valore del debito, la prima proposizione del teorema diventa:
Il significato dell'espressione sopra è che le imprese possono trarre vantaggio dall'indebitamento, dal momento che possono dedurre dal pagamento delle imposte sugli utili i pagamenti di interessi, così che l'indebitamento riduce il livello di tassazione; per contro, i pagamenti di dividendi agli azionisti, che costituiscono interamente il costo del capitale per un'impresa che non ha debito, non sono di norma deducibili ai fini fiscali.
L'espressione sopra si presta inoltre a un'interpretazione intuitiva: si ipotizzi che il debito dell'impresa abbia maturità «infinita», sicché l'impresa versa in perpetuo, ogni anno, ai suoi creditori, un interesse pari a ; il beneficio in termini di tassazione (il pagamento di interessi è infatti deducibile) sarà allora . Il valore attuale di una rendita perpetua con rata è, per un tasso d'interesse pari a :
appunto l'ammontare per cui eccede . In altre parole: la presenza di debito incrementa il valore dell'impresa per un ammontare pari al valore attuale dei vantaggi fiscali che l'impresa deriva dal debito.
La seconda proposizione diventa inoltre:
con analoga interpretazione al caso precedente.
Risultato di Modigliani-Miller e CAPM[modifica | modifica wikitesto]
Si ipotizzi inoltre che il CAPM sia valido; ciò implica che il rendimento di qualunque attività finanziaria si esprime come:
dove denota il rendimento privo di rischio, il rendimento atteso del mercato, e:
Sostituendo nell'espressione per il rendimento della levered company, si ha:
ossia:
Sotto l'ipotesi (comunemente effettuata nei libri di testo) che il debito sia privo di rischio, , così che l'espressione per il beta del capitale di rischio (equity) della levered company si riduce a:
Un'applicazione: riacquisto di azioni proprie finanziato tramite emissione di debito[modifica | modifica wikitesto]
Si consideri un'impresa inizialmente priva di debito. Il business dell'impresa genera in perpetuo un flusso di cassa pari a 10 000 euro ogni anno, al netto delle imposte; le azioni dell'impresa hanno un beta , il tasso d'interesse privo di rischio è e il rendimento atteso del mercato è . Ipotizzando che il CAPM sia valido, il tasso di rendimento richiesto dall'investitore rappresentativo al fine di detenere azioni dell'impresa sarà:
Il valore dell'impresa può essere allora calcolato utilizzando il metodo del WACC la formula per una rendita perpetua: dal momento che l'impresa genera una rendita perpetua con cedola pari a 10 000 euro ogni anno, scontando la rendita al tasso si ottiene:
il valore dell'impresa priva di debito.
Si ipotizzi a questo punto che il reddito dell'impresa sia soggetto a un'aliquota d'imposta , e che l'impresa intenda riacquistare 40 000 euro di azioni proprie, emettendo contestualmente 40 000 euro di debito. In assenza di tassazione, quest'operazione lascerebbe inalterato il valore dell'impresa: si tratterebbe semplicemente di rimpiazzare una fonte di finanziamento (il capitale proprio) con una alternativa (il debito). Dal momento che vi è imposizione fiscale, tuttavia, l'operazione crea valore; nello specifico, il valore dell'impresa diviene:
utilizzando la proposizione di Modigliani-Miller in presenza di tassazione.
Struttura ottimale del capitale e costi attesi d'insolvenza[modifica | modifica wikitesto]
La conclusione dell'estensione del teorema originario all'ipotesi di un'economia con tasse è che le imprese traggono un vantaggio, in termini di imposizione fiscale, dal debito. In assenza di svantaggi a controbilanciare il guadagno fiscale derivante dal debito, le imprese dovrebbero finanziare i loro investimenti esclusivamente tramite debito.
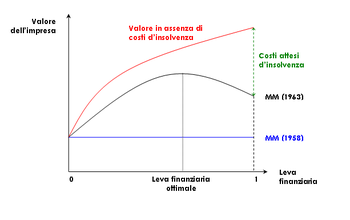
Naturalmente quest'ultima conclusione non è realistica, da un punto di vista positivo — in genere, le imprese fanno anche ricorso al capitale di rischio, o equity — né da un punto di vista normativo — sarebbe rischioso per le imprese indebitarsi oltre misura. Modigliani e Miller mettono le mani avanti, consci del fatto che il loro elegante modello presta il fianco a tali critiche; nello stesso lavoro in cui sviluppano le due proposizioni in presenza di tassazione, sottolineano come un aumento del debito innescherà inevitabilmente dei costi, derivanti ad esempio da un aumento parallelo della probabilità di insolvenza dell'impresa, che andranno a bilanciare i vantaggi fiscali. La soluzione del trade-off tra vantaggio fiscale e svantaggio derivante dalla probabilità di insolvenza determinerà una struttura ottimale del capitale. Questo risultato altro non è che la prima espressione di una serie di teorie della struttura ottimale del capitale che vanno sotto il nome comune di teorie del trade-off.
Bibliografia[modifica | modifica wikitesto]
Contributi originali[modifica | modifica wikitesto]
- (EN) Franco Modigliani; Merton Miller, The Cost of Capital, Corporate Finance, and the Theory of Investment, in American Economic Review, vol. 3, n. 48, giugno 1958, pp. 261-297.
- (EN) Merton Miller; Franco Modigliani, Corporate Income Taxes and the Cost of Capital: A Correction, in American Economic Review, vol. 3, n. 53, 1963, pp. 433-443.
Manualistica[modifica | modifica wikitesto]
- (EN) Richard A. Brealy; Stewart C. Myers; Franklin Allen, Principles of Corporate Finance, New York, McGraw-Hill Irwin, 2006, ISBN 0-07-255274-3. Un manuale per i practitioner e gli studenti di corsi universitari e di master in business administration.
- (EN) Jean Tirole, The Theory of Corporate Finance, Princeton University Press, 2006, ISBN 0-691-12556-2. Un manuale dall'approccio più teorico, diretto al ricercatore.
Voci correlate[modifica | modifica wikitesto]
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) Modigliani-Miller theorem, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.




















![{\displaystyle R_{i}=R_{f}+\beta _{i}\left({\mbox{E}}[R_{m}]-R_{f}\right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/c497341a9b4c513d3e871ee2427fb2c1e6202098)

![{\displaystyle {\mbox{E}}[R_{m}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/82d0a7e5765b364f4d2d3bd6d5db06e5f4b1188d)

![{\displaystyle R_{f}+\beta _{L}({\mbox{E}}[R_{m}]-R_{f})=R_{f}+\beta _{U}({\mbox{E}}[R_{m}]-R_{f})+{\frac {D}{E}}\left[R_{f}+\beta _{U}({\mbox{E}}[R_{m}]-R_{f})-R_{f}-\beta _{D}({\mbox{E}}[R_{m}]-R_{f})\right](1-T_{C})}](https://wikimedia.org/api/rest_v1/media/math/render/svg/222b1b0aa38ed0d56821c0feb611c28796d05acf)


![{\displaystyle \beta _{L}=\beta _{U}\left[1+(1-T_{C}){\frac {D}{E}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6dfc48df45d822ce0d433e96e81f4a16d237a079)







