Statica delle strutture
La statica delle strutture è la parte della meccanica che sviluppa lo studio statico di corpi riconducibili a forme strutturali note nella meccanica delle strutture, in particolare travi e travature. Interesse prevalente è lo studio delle strutture isostatiche, le sole per le quali, attraverso le sole condizioni di equilibrio statico, è possibile pervenire ad una determinazione completa del loro stato di sollecitazione interna. Tale studio oggigiorno è svolto prevalentemente per via analitica e numerica. Nel passato molto utilizzati risultavano gli strumenti della statica grafica, adesso richiamati saltuariamente e solo a fini didattici.
Condizioni di equilibrio di una struttura[modifica | modifica wikitesto]
Una struttura in un'assegnata configurazione geometrica è in equilibrio se tale equilibrio sussiste per ognuna delle parti in cui la struttura può essere decomposta. Il problema dell'equilibrio statico di una struttura può essere pertanto ricondotto al problema dell'equilibrio statico di tutte le sue parti. In tali relazioni di equilibrio intervengono non solo le forze (e le coppie) esterne applicate, ma anche le azioni (le sollecitazioni interne) che le varie parti si scambiano reciprocamente. Ai fini della valutazione dell'equilibrio, le varie parti della struttura possono essere riguardate come corpi rigidi.
Equazioni cardinali della statica[modifica | modifica wikitesto]
Condizione necessaria e sufficiente affinché un corpo rigido risulti in equilibrio è che siano nulli:
- il risultante delle forze applicate (equilibrio alla traslazione), cioè la sommatoria delle forze dovrà essere uguale a 0
- il risultante dei momenti delle forze e delle coppie applicate (equilibrio alla rotazione), allo stesso modo anche la sommatoria dei momenti dovrà essere uguale a 0
Per un corpo nello spazio tridimensionale, le equazioni cardinali della statica corrispondono a 6 equazioni scalari (3 alla traslazione e 3 alla rotazione). Nel caso piano (le traiettorie dei punti del corpo appartengono ad un piano, ove sono contenute le forze applicate), le equazioni della statica corrispondono a 3 equazioni scalari (due alla traslazione e una alla rotazione (attorno ad una direzione normale al piano del problema).
Per un sistema composto da un numero generico c di parti, dovendo le equazioni della statica valere per ognuna delle sue parti, il loro numero complessivo è 6c nel caso tridimensionale e 3c nel caso piano.
I gradi di libertà[modifica | modifica wikitesto]
Dicesi grado di libertà il numero di parametri cinematici necessari a caratterizzare il moto o l'atto di moto di un sistema. Un corpo rigido nello spazio tridimensionale ha 6 gradi di libertà (3 alla traslazione e 3 alla rotazione). Nel problema piano, il corpo rigido ha 3 gradi di libertà (due alla traslazione e una alla rotazione).
La cinematica di un sistema composto da c corpi rigidi è definita dalla cinematica di ogni corpo del sistema. Il suo grado di libertà è la somma quindi dei gradi di libertà delle sue parti.
Il grado di libertà di un sistema eguaglia il numero di equazioni scalari necessarie ad imporre l'equilibrio
Un vincolo è ogni impedimento alla libera mobilità dei corpi. In statica delle strutture i vincoli considerati sono:
- olonomi (impongono restrizione alla sola posizione dei corpi);
- fissi (sono indipendenti dal tempo);
- bilateri (ogni componente cinematica impedita lo è in entrambi i versi);
- privi di attrito (consentono integralmente i movimenti a cui non si oppongono).
I vincoli si dicono esterni se limitano gli spostamenti assoluti, interni se limitano gli spostamenti relativi tra le parti di un sistema. Si dice grado di vincolo il numero di componenti di spostamento vincolate: in questo senso si parla di vincolo semplice se limita una sola componente di spostamento, di vincolo doppio, triplo... quando le componenti impedite sono più d'una.
Si parla di cedimento vincolare quando il vincolo impone, alla componente di spostamento vincolata, di assumere un determinato valore non nullo.
In Meccanica, i vincoli sono equivalenti a delle forze, in quanto modificano il moto di un sistema ogniqualvolta questo cerchi di violarli. Dicesi reazione vincolare la forza esplicata da un vincolo. Affinché si possa esercitare la condizione di vincolo cinematico, le reazioni vincolari hanno una ben precisa caratterizzazione in funzione della componente di spostamento che deve essere vincolata: ciò determina alcuni caratteri vettoriali (direzione e punto di applicazione) delle reazioni vincolari, e quindi il numero di parametri scalari indipendenti (il grado di vincolo) attraverso cui si esprime la reazione vincolare.
Tipi di vincoli[modifica | modifica wikitesto]


Per problemi piani, i vincoli più comunemente utilizzati in statica delle strutture sono di seguito descritti.
- il carrello o appoggio semplice è un vincolo semplice ed impedisce lo spostamento del punto vincolato lungo l'asse ortogonale al piano di scorrimento del carrello. Lascia al corpo due libertà di movimento: la traslazione lungo il piano di scorrimento del carrello e la rotazione attorno al punto vincolato. La reazione vincolare corrisponde ad una forza applicata nel punto vincolato e diretta lungo la direzione ortogonale al piano di scorrimento.
- la cerniera è un vincolo doppio che impedisce lo spostamento del punto vincolato lungo una qualsiasi direzione del piano del problema. Lascia il corpo libero di ruotare intorno al punto stesso. Reagisce con una forza applicata al punto e diretta secondo una qualsiasi direzione appartenente al piano del problema: tale forza può essere rappresentata dalle sue due componenti su due assi ortogonali.
- l’incastro è un vincolo triplo che impedisce al corpo sia le due componenti di traslazione che la rotazione. Reagisce attraverso due componenti di forza su due diverse direzioni e una coppia.
- il pendolo o biella è un vincolo semplice equivalente del carrello: impedisce gli spostamenti del punto vincolato lungo l'asse della biella e permette al corpo gli spostamenti ortogonali a tale asse e la rotazione attorno al punto. Reagisce con una forza applicata al punto e diretta lungo l'asse della biella.
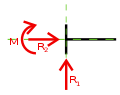
- il doppio pendolo o bipendolo è un vincolo doppio che impedisce la traslazione lungo l'asse dei pendoli e la rotazione del corpo. Permette al corpo di traslare lungo la direzione ortogonale all'asse dei pendoli: in tal senso il vincolo viene detto anche pattino o glifo. Reagisce con una forza diretta secondo l'asse del pendolo ed una coppia.
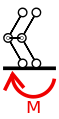
- il doppio doppio pendolo o quadripendolo o pendolo improprio o pantografo è un vincolo semplice che impedisce le rotazioni del corpo. Lascia libero il corpo di traslare. Reagisce tramite una coppia.
-
Il carrello
-
La cerniera
-
L'incastro
-
Il pendolo
-
Il doppio pendolo
-
Il doppio doppio pendolo
Sistemi vincolati[modifica | modifica wikitesto]
Dicesi vincolato un sistema meccanico (una struttura), composto da più corpi (le parti della struttura), soggetto ad un sistema di vincoli cinematici. Il grado di vincolo m del sistema è la somma del grado dei singoli vincoli. Per spostamenti infinitesimi rigidi delle parti della struttura, la presenza di vincoli cinematici è in generale espressa da un sistema di m equazioni algebriche lineari negli n parametri cinematici che descrivono la libera mobilità della parti della struttura (n è il grado di libertà del sistema)
dove sono gli eventuali cedimenti assegnati dei vincoli. La matrice A (m x n) dei coefficienti è detta matrice cinematica del sistema.
Per un sistema vincolato, il problema dell'equilibrio si traduce in un sistema di n equazioni algebriche lineari nell'insieme degli m parametri rappresentativo delle reazioni vincolari:
ove sono i termini noti delle equazioni legati agli assegnati valori delle forze e delle coppie esterne agenti sul sistema. La matrice B (n x m) dei coefficienti è detta matrice di equilibrio, o matrice statica. Si dimostra che, per una opportuna scelta dei parametri , la matrice di equilibrio è pari alla trasposta della matrice cinematica
Caratterizzazione statica e cinematica dei sistemi vincolati[modifica | modifica wikitesto]



I sistemi meccanici si caratterizzano staticamente e cinematicamente sulla base delle soluzioni possibili dei sistemi di equazioni che rappresentano rispettivamente le condizioni di equilibrio del sistema e l'azione cinematica dei vincoli
e quindi sulla base delle proprietà algebriche delle due matrici A e B dei coefficienti che intervengono nel problema. Detto p il rango di tali matrici (il rango delle due matrici coincide essendo una la trasposta dell'altra), si hanno le seguenti tipologie:
- sistema isostatico (p=n=m): il grado di vincolo eguaglia il grado di libertà e i vincoli sono ben posti, cioè tra loro indipendenti. Il problema statico (così come il problema cinematico) ammette soluzione e la soluzione è unica: si dice allora che il sistema è staticamente determinato (a qualsiasi valore dei carichi esterni sono associate reazioni vincolari che rendono il sistema equilibrato) e cinematicamente determinato (i vincoli sono strettamente sufficienti ad impedire atti di moto rigido delle sue parti, o a determinarli univocamente nel caso di cedimenti assegnati).
- sistema labile (p=m<n) : il grado di vincolo è inferiore al grado di libertà del sistema e i vincoli presenti sono ben posti. In termini cinematici, il relativo problema ammette soluzioni: i vincoli applicati, sono insufficienti ad impedire atti di moto rigido del sistema, capaci di articolarsi secondo l=n-m meccanismi di labilità (il sistema è cinematicamente indeterminato ed l=n-m è il grado di labilità). In termini statici, il relativo problema non ammette in generale soluzione. Sono possibili due situazioni, che dipendono dal rango p' della matrice ottenuta orlando la matrice statica con il vettore dei termini noti. Se p'>p il sistema è staticamente impossibile. Se p'=p il sistema (pur cinematicamente labile) è staticamente determinato. La classificazione statica dipende quindi dal sistema di carico presente.
- sistema iperstatico (p=n<m): il grado di vincolo è superiore al grado di libertà. In termini statici, il relativo problema ammette soluzioni: il sistema è sempre in equilibrio ma le condizioni di equilibrio sono in numero insufficiente a determinare univocamente i valori delle reazioni vincolari (il sistema è staticamente indeterminato ed i=m-n è il suo grado di iperstaticità). In termini cinematici, il relativo problema non ammette in generale soluzione per generici valori dei cedimenti: i vincoli sono sovrabbondanti e gli atti di moto del sistema sono sempre impediti.
- sistema degenere (p<min{n,m}): i vincoli presenti sono malposti ed insufficienti ad impedire atti di moto del sistema (il sistema ha n-p meccanismi di labilità). L'equilibrio sussiste solo per particolari valori dei carichi (p'=p), ma il numero p di equazioni indipendenti di equilibrio non è sufficiente a determinare univocamente il valori delle reazioni vincolari (il sistema ha m-p iperstaticità). In pratica un sistema degenere presenta contemporaneamente meccanismi di labilità e condizioni di iperstaticità.
Strutture isostatiche, iperstatiche e labili[modifica | modifica wikitesto]
Per una generica struttura è sempre verificata la relazione tra grado di libertà, di vincolo, di labilità e di iperstaticità
Da ciò si traggono le seguenti condizioni sufficienti per la labilità e l'iperstaticità di una struttura:
- la struttura è sicuramente labile;
- la struttura è sicuramente iperstatica.
Le due condizioni non sono tuttavia necessarie per la labilità e l'iperstaticità: un sistema degenere presenta sia iperstaticità sia labilità, pur avendo .
D'altra parte l'uguaglianza tra grado di libertà e grado di vincolo risulta una condizione necessaria ma non sufficiente per la isostaticità:
- la struttura è isostatica.
I vincoli infatti possono essere mal posti e la struttura risulterà in effetti degenere. In conclusione una struttura è isostatica se c'è uguaglianza tra grado di vincolo e grado di libertà e se si dimostra che i vincoli sono efficaci, cioè se si dimostra che sono assenti meccanismi di labilità della struttura.
Le strutture isostatiche rivestono un ruolo prevalente in statica delle strutture, in quanto esse sono univocamente risolvibili (in termini di reazioni vincolari e di sforzi di sollecitazione interna) mediante il solo utilizzo delle condizioni di equilibrio statico.
Per le strutture iperstatiche, le sole equazioni della statica non sono sufficienti per una loro risoluzione: in tal caso occorre fare riferimento al metodo delle forze o al metodo delle rigidezze.
Le strutture labili sono, in generale, staticamente irrisolvibili.
Le caratteristiche di sollecitazione[modifica | modifica wikitesto]

Un corpo (una trave) in equilibrio sotto l'azione di un sistema di forze esterne, può sempre pensarsi composto da due parti definite da un piano di sezionamento. Il vincolo di continuità agisce in corrispondenza della sezione imponendo che le due parti permangano combacianti durante il moto del corpo. Tale vincolo di continuità si esplica sulla sezione mediante un sistema puntuale di sollecitazioni (le tensioni interne) che le due parti del corpo si scambiano reciprocamente attraverso le due facce della sezione.
Le forze di contatto che una parte del corpo esercita sull'altra intervengono, assieme alle forze esterne applicate, nelle condizioni di equilibrio che devono continuare a valere per ognuna delle due parti del corpo. Pertanto il risultante ed il momento risultante delle forze di contatto interne sono determinabili sulla base delle equazioni cardinali delle statica di una delle due parti del corpo, equilibrando il risultante ed il momento risultante delle forze esterne ivi applicate.
Si dicono caratteristiche di sollecitazione di una sezione le componenti dei vettori del risultante e del momento risultante delle forze di contatto interne della sezione, in un riferimento locale solidale al piano della sezione. Per un problema piano esse sono:
- sforzo normale (N) (componente del risultante delle forze di contatto nella direzione perpendicolare alla faccia della sezione)
- sforzo di taglio (T) (componente del risultante delle forze di contatto nella direzione parallela alla faccia della sezione)
- momento flettente (M) (componente del momento risultante nella direzione normale al piano del problema)
Le caratteristiche di sollecitazione variano al variare della sezione. Una loro rappresentazione sintetica è ottenibile mediante diagrammi. In strutture piane, obiettivo primario della statica delle strutture è la ricostruzione dei diagrammi dello sforzo normale, dello sforzo di taglio e del momento flettente.
Bibliografia[modifica | modifica wikitesto]
- Belluzzi Odone, Scienza delle Costruzioni (1º volume), Zanichelli, Bologna, 1953 e successive edizioni
- Giulio Ceradini. Scienza delle costruzioni. 1: Cinematica e statica dei sistemi rigidi. ESA, Roma, 1985. ISBN 88-405-3017-7.
- Elisa Guagenti Grandori et al. Statica. McGraw-Hill, Milano, 1995. ISBN 88-386-0657-9.
- Antonio Domenico Lanzo. Analisi di Travature Elastiche: metodi e applicazioni. Aracne, Roma, 2007. ISBN 978-88-548-1162-1.