Scelta intertemporale
Nella teoria del consumatore, la scelta intertemporale è la decisione dell'individuo concernente l'allocazione del consumo, del risparmio e del lavoro tra il presente e il futuro (distribuzione nel tempo).
Il modello di Fisher[modifica | modifica wikitesto]
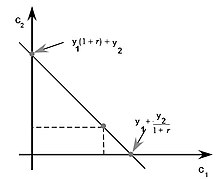
Il modello di Fisher può essere illustrato prendendo due periodi: il periodo attuale o periodo 1 (questo mese o quest'anno) e il periodo futuro o periodo 2 (il mese prossimo o l'anno prossimo). L'individuo pianifica il suo consumo tenendo conto dei suoi bisogni e dei suoi redditi attuali e previsti. Il vincolo di bilancio è:
dove è il consumo attuale e il consumo futuro; il reddito attuale e il reddito futuro. La somma risparmiata (se questa differenza è positiva) o presa in prestito (se questa differenza è negativa) è investita o presa in prestito al tasso di interesse . Le preferenze del consumatore sono rappresentate dalla funzione di utilità intertemporale . Si ottiene la massima utilità con il metodo di Lagrange:
dove è una variabile ausiliaria. Le condizioni di primo ordine sono:



Risolvendo questo sistema di equazioni si ottengono le funzioni di consumo:
Dalle condizioni di primo ordine si può anche dedurre la relazione seguente:
Il termine a sinistra è chiamato il tasso di preferenza intertemporale. All'equilibrio deve essere uguale al tasso di interesse[1].
Graficamente, la soluzione è ottenuta quando la curva d'indifferenza più alta è tangente alla retta del vincolo di bilancio (punto A).
Variazione del tasso di interesse[modifica | modifica wikitesto]
Se il tasso di interesse aumenta la retta del vincolo di bilancio subisce una rotazione oraria con perno il punto dove il consumo di ogni periodo è uguale al reddito del periodo (punto E).
Questa variazione ha un effetto di reddito[2] (il consumatore che ha risparmiato nel periodo 1 avrà un reddito più grande nel periodo 2) e un effetto di sostituzione[3] (risparmiare diventa più vantaggioso poiché l'interesse aumenta)[4]. Se il consumatore voleva prendere un prestito, l'effetto totale è una diminuzione del consumo nel periodo 1. In caso di risparmio, l'effetto totale è ambiguo.
Utilizzando la teoria della preferenza rivelata, si può anche dire che un consumatore che risparmia resta sempre un risparmiatore quando il tasso di interesse aumenta. Se il tasso di interesse diminuisce, il consumatore che ha preso un prestito continua a essere un debitore nel periodo 1[5].
Tutti questi risultati sono valevoli solo nel caso di due periodi. Se ci sono altri periodi non si è obbligati a rimborsare il prestito nel periodo 2.
La regola di Keynes-Ramsey[modifica | modifica wikitesto]
Si fa sovente l'ipotesi che la funzione di utilità intertemporale è di forma additiva nei periodi:
dove è il “tasso soggettivo di sconto del tempo” e l'utilità istantanea. L'idea di uno «sconto soggettivo» delle utilità future come per i valori finanziari risale a Böhm-Bawerk. Secondo questo autore[6] la sottovalutazione dei beni futuri[7] è dovuta alla mancanza d'immaginazione e ad una debolezza della volontà degli individui.
Sostituendo prendendo il valore dedotto dal vincolo di bilancio si ottiene la condizione di primo ordire per la massimizzazione della funzione di utilità intertemporale:
Prendendo questa equazione intertemporale di Eulero si ottiene la regola di Keynes-Ramsey[8]:
Il tasso marginale di sostituzione intertemporale deve essere uguale al prezzo relativo dei consumi.
Generalizzazione con tempo continuo[modifica | modifica wikitesto]
Nel caso di numerosi periodi si preferisce sovente utilizzare il tempo continuo. La funzione di utilità intertemporale diventa allora:
La variazione del consumo dipende dall'equazione differenziale:
dove sono gli attivi finanziari, il reddito non finanziario (reddito del lavoro per esempio), il consumo e il punto sopra la variabile indica la derivata rispetto al tempo. Siccome i valori finanziari futuri non possono avere un valore attuale negativo, bisogna imporre la restrizione:
(niente schema Ponzi)
Utilizzando il metodo di Pontryagin si ha il valore corrente dell'hamiltoniana:
dove è una variabile ausiliaria. Dopo avere sostituito questa variabile nelle condizioni di primo ordine[9] [10] si ottiene la regola di Keynes-Ramsey:
dove:
Il tasso di crescita ottimale del consumo dipende dall'elasticità di sostituzione intertemporale e dall'eccedenza del tasso di interesse rispetto al tasso soggettivo di sconto intertemporale.
Sconto iperbolico[modifica | modifica wikitesto]
Gli esperimenti effettuati con degli studenti trovano che la sottovalutazione dei beni futuri non segue una legge esponenziale come supposto qui sopra. Per esempio Thaler[11] ha osservato che, quale valore mediano, gli studenti chiedono, al posto di 15 $ immediatamente, 20 $ se un mese dopo, 50 $ se un anno dopo e 100 $ se dieci anni dopo. Questi valori implicano uno sconto di 347% per un mese, 120% per un anno e 19% per 10 anni. Una diminuzione del tasso di sconto con lo scorrere del tempo può essere rappresentato da una legge iperbolica:
Quando tende verso zero si ritrova lo sconto esponenziale: .
Questo tipo di sconto, preferito dagli psicologi[12], conduce ad una incoerenza intertemporale[13]. Il consumatore non segue il piano di consumo previsto precedentemente anche nel caso in cui niente cambia eccetto il tempo trascorso. La preparazione di un piano di consumo non ha grande utilità se lo sconto è iperbolico.
Modello del ciclo vitale di Modigliani[modifica | modifica wikitesto]
Il punto di partenza della teoria del ciclo vitale è il modello di Fisher con un orizzonte temporale corrispondente a tutta la vita di un consumatore. Supponiamo che il reddito annuale sia costante e uguale a fino all'anno di pensionamento e zero in seguito. Se il consumatore vive anni, il consumo uniforme sarà di (supponendo un tasso di interesse nullo). Il consumatore risparmia ogni anno , fino al pensionamento, e in seguito utilizzerà il risparmio accumulato per il consumo durante gli anni in pensione.
Nel caso più generale[14], sia il valore attuale dei redditi previsti l'anno t dall'individuo di T anni:
dove è il capitale accumulato, i redditi previsti e r il tasso di interesse.
Se la funzione di utilità è omogenea rispetto ai consumi, si ottiene la funzione di consumo seguente:
dove è il reddito medio previsto e un fattore proporzionale che dipende dalla funzione di utilità.
Il modello può essere generalizzato introducendo il risparmio a scopo di eredità, la sicurezza sociale o una durata di vita aleatoria.
La teoria di Modigliani è utilizzata per studiare i sistemi di pensione pubblici e privati e il legame tra risparmio e crescita[15].
Il modello di Friedman[modifica | modifica wikitesto]
Secondo Friedman[16] il consumo dipende dal reddito permanente dell'individuo, cioè dal reddito medio a lungo termine:
dove è il consumo (permanente) e è un coefficiente che dipende dal tasso di interesse, dal tasso di sconto soggettivo intertemporale e dal rapporto tra il patrimonio e il reddito del consumatore.
Sia il consumo dell'individuo i al tempo t. Si ha:
dove è il consumo transitorio. Inoltre:
- .
Ciò significa che il reddito transitorio non ha nessun effetto sul consumo globale.
Friedman suppone che non ci sia correlazione tra alcune di queste variabili, in particolare tra il reddito transitorio e il consumo transitorio:
dove è il coefficiente di correlazione.
Friedman propone di stimare il reddito permanente utilizzando la tecnica dei ritardi distribuiti:
dove sono dei coefficienti.
Le stime ottenute con dati aggregati ottengono una variazione del consumo superiore al valore previsto dalla teoria del reddito permanente (variazione eccessiva del consumo)[17].
Le stime con i dati individuali danno un risultato assai soddisfacente per la teoria del reddito permanente e quella del ciclo vitale[18].
Note[modifica | modifica wikitesto]
- ^ Fisher Irving, The Theory of Interest, New York, 1907, p. 291
- ^ Da D a B
- ^ Da A a D
- ^ J.M. Henderson and R.E. Quandt, Microeconomic Theory, London, 1980, p.331
- ^ Hal R. Varian, Intermediate Microeoconmics, London, 2009
- ^ Eugen von Böhm-Bawerk, Kapital und Kapitalzins, Innsbruck, 1914
- ^ Una vacanza tra un anno ha meno utilità di una vacanza oggi.
- ^ Frank Ramsey, « A Mathematical Theory of Saving », Economic Journal, 1928, pp. 543-559
- ^ :
- ^ La condizione di trasversalità deve essere soddisfatta:
- ^ Richard Thaler, « Some empirical evidence on dynamic inconsistency «, Economic Letters, 1981, pp. 201-207
- ^ Shane Frederick et al., « Time discounting and time preference: A critical review », Journal of economic literature, 2002, pp. 351-401
- ^ Robert Strotz, « Myopia and Inconsistency in Dynamic Utility Maximisation «, Review of Economic Studies, 1956, pp. 165-180
- ^ Francesco Franco et. al., The Collected Papers of Franco Modigliani, vol. 6, Boston, 2005, p. 49
- ^ Angus Deaton, « Franco Modigliani and the life-cycle theory of consumption »,.BNL Quarterly Review, 2005, pp. 91-107
- ^ Milton Friedman, A Theory of the Consumption Function, Princeton, 1957
- ^ John Campbell and Gregory Mankiw, « Permanent Income, Current Income, and Consumption », Journal of Business and Economic Statistics, 1990, pp. 265-279
- ^ Orazio Attanasio and Martin Browning, « Testing the Life Cycle Model of Consumption: what can we learn from micro and macro data », Investigaciones Economicas, 1994, pp. 433-463
Bibliografia[modifica | modifica wikitesto]
- Olivier Blanchard and Stanley Fischer, Lectures on Macroeconomics, Boston, 1989
- Gernot Doppelhofer, «Intertemporal Macroeconomics », in N.F.G. Allington and J.S.L. McCombie, Cambridge Essays in Applied Economics, Cambridge, 2003
- Rudiger Dornbusch and Stanley Fischer, Macro-Economics, London, 1981
- Hal R. Varian, Intermediate Microeconomics, London, 2009








![{\displaystyle L=V(C_{1},C_{2})+\lambda \left[Y_{1}(1+r)+Y_{2}-C_{1}(1+r)-C_{2}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d4ced5bc2f866594cbafea3db029f6d12c550b72)

















![{\displaystyle {\mathcal {H}}^{c}=u(C_{t})+\lambda \left[rA+Y-C\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7e5a10ee27b7b1e9cfc5249532eaa57b9c8c1cfb)


![{\displaystyle \left[1/\theta (C)\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2350e74d615a4bdb9eabd796470c57af16d2eff1)






![{\displaystyle \left[{\frac {N}{L}}{\bar {Y}}\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/db9aed8ea816ba932611a3a2366a2d26e96500bd)



















![{\displaystyle {\dot {\lambda }}=\rho \lambda -{\frac {\partial {\mathcal {H}}^{c}}{\partial A}}=\lambda \left[\rho -r\right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/60369195aeee73393f840f6063b21104f34ec678)
