Nonogram

I Nonogram oppure Paint by Numbers (dipingere con i numeri) o griddlers, sono dei rompicapi logici grafici in cui le celle di una griglia devono essere colorate o lasciate in bianco in base a dei numeri a lato della griglia utili a svelare un'immagine nascosta. In questo tipo di rompicapo, il numero indica quante celle consecutive devono essere riempite, o in riga, o in colonna. Per esempio, un indizio del tipo "4 8 3" significa che c'è un insieme di quattro, otto e tre quadrati da riempire in questo ordine, con almeno un quadrato bianco tra gruppi successivi.
Questi rompicapi sono spesso nella modalità bianco e nero, ma possono essere anche nelle versioni con più colori. Se questi sono colorati, allora il numero degli indizi saranno colorati in base al colore dei quadrati da riempire (in base al colore). Due numeri di colore diverso possono o non possono avere spazi tra di loro. Ad esempio, un quattro nero seguito da un due rosso potrebbe significare, o quattro spazi neri, o alcuni spazi vuoti, o due spazi rossi, oppure potrebbe semplicemente significare avere quattro spazi neri seguiti immediatamente da due spazi rossi.
Non c'è teoricamente un limite alla dimensione di un nonogram, e la struttura non è necessariamente una forma quadrata.
Nomi[modifica | modifica wikitesto]
I Nonogram sono anche conosciuti in molti altri nomi, includendo Paint by Numbers, Griddlers, Pic-a-Pix, Picross, Pixel Puzzles, Crucipixel, Edel, FigurePic, gameLO, Grafilogika, Hanjie, Illust-Logic, Japanese Crosswords, Japanese Puzzles, Kare Karala!, Logic Art, Logic Square, Logicolor, Logik-Puzzles, Logimage, Obrazki logiczne, Zakódované obrázky, Maľované krížovky, Oekaki Logic, Oekaki-Mate, Paint Logic, Shchor Uftor, Gobelini, e Tsunamii. Essi sono stati chiamati anche con Paint by Sudoku e Binary Coloring Books, anche se questi nomi non sono del tutto esatti.
Tecniche di soluzione[modifica | modifica wikitesto]
Per poter risolvere un rompicapo, si deve determinare quali celle siano da colorare e quali siano vuote. Durante il processo di risoluzione, gli spazi aiutano a determinare dove un indizio può essere propagato. I risolutori generalmente usano dei puntini o delle crocette per marcare le celle che sono sicuramente degli spazi.
Molto importante è cercare di non indovinare la disposizione delle celle. Solo le celle che possono essere determinata dalla logica possono essere riempite. Se si cerca di indovinare, un singolo errore può propagarsi nella griglia a tal punto di rovinare completamente la soluzione. Errori del genere si notano solo dopo un po' di tempo ed è molto difficile correggere il puzzle. Generalmente, solo i più grandi ed esperti risolutori sono in grado di correggere un problema del genere.
La figura nascosta non svolge nessun compito durante il processo di soluzione. Anche se ad un certo punto l'immagine nascosta è ormai evidente, generalmente non bisogna far affidamento a tale immagine. L'immagine, tuttavia, può aiutare a cercare ed eliminare degli errori.
I semplici puzzle possono essere usualmente risolti da un ragionamento su una singola riga (o singola colonna) in ogni dato periodo di tempo, per determinare, per riga (o per colonna) , più celle riempite o vuote possibili. Poi si prova un'altra riga (o colonna) fino a quando non vi sono righe (o colonne) che contengono celle indeterminate.
Alcuni puzzle complicati possono anche richiedere diversi tipi di ragionamento del tipo "cosa succede se?", che includono più di una riga (o più colonne). Questa tecnica lavora per contraddizione: "Quando una cella non può essere riempita poiché altre celle produrrebbero un errore, allora questa diventerà definitivamente uno spazio. E viceversa."
Semplici caselle[modifica | modifica wikitesto]
All'inizio del processo di risoluzione, un semplice metodo può essere usato per determinare più caselle possibili. Questo metodo usa delle congiunzioni di possibili posti per ogni possibile blocco di caselle. Ad esempio, in una riga di dieci celle con un solo indizio "8", il blocco da 8 caselle può essere così considerato:

- nel bordo di destra, lasciando 2 spazi alla sinistra;
- nel bordo di sinistra, lasciando 2 spazi alla destra;
- o da qualche parte nel mezzo.
Di conseguenza, un pezzo del blocco sarà, dovuto alla congiunzione, posto nel centro.
Lo stesso procedimento può essere applicato quando ci sono più aiuti in una determinata riga. Ad esempio, in una riga con dieci celle con indizi di "4" e "3", i blocchi di caselle possono essere:

- disposti tutti a sinistra, lasciando un solo spazio vuoto tra i due gruppi, lasciando due spazi vuoti alla destra;
- disposti tutti a destra, lasciando un solo spazio vuoto tra i due gruppi, lasciando due spazi vuoti alla sinistra;
- o da qualche parte nel mezzo.
Di conseguenza, il primo blocco di quattro caselle sicuramente include nella soluzione la terza e la quarta cella, mentre il secondo blocco di tre caselle, include solamente l'ottava cella. Le caselle possono pertanto essere piazzate nella terza, quarta ed ottava cella. Nota importante: quando si determinano le caselle in questa maniera, le caselle possono essere piazzate in celle solamente se c'è una sovrapposizione di blocchi; in questo esempio, sebbene ci sia una sovrapposizione nella sesta cella, questi sono differenti blocchi, e così non si può ancora sapere se la sesta cella conterrà o no una casella.
Semplici spazi[modifica | modifica wikitesto]
Questo metodo consiste nel determinare gli spazi per la ricerca di celle che sono fuori dal range per qualche possibile blocco di caselle. Ad esempio, si consideri una riga di dieci celle con caselle nella quarta e nona cella, e con indizi di "3" ed "1".

In primo luogo, l'indizio "1" è completo e ci sarà uno spazio in ogni lato del blocco. In secondo luogo, l'indizio "3" può solo aiutare a cercare caselle tra la seconda e la sesta cella, poiché la quarta cella è una casella; tuttavia, questo comporta che alcune celle non possono essere caselle in ogni caso, cioè la prima e la settima cella, che saranno degli spazi.
Forzatura[modifica | modifica wikitesto]
In questo metodo, sarà mostrato il significato degli spazi. Uno spazio piazzato in qualche posto nel centro di una riga incompleta, può forzare un largo blocco ad uno dei lati. Inoltre, un gap troppo piccolo per qualche blocco, può essere riempito da spazi.

Ad esempio, si consideri una riga di dieci caselle con spazi nella quinta e settima cella, e con indizi di "3" e "2":
- l'indizio "3" forza il primo blocco alla sinistra, poiché non può essere piazzato altrimenti; in questo caso, la seconda e terza cella, saranno caselle;
- lo spazio vuoto nella sesta cella è troppo piccolo per blocchi da due e tre, e quindi può essere riempito da spazi;
- infine, l'indizio "2" porterà ad una casella alla nona cella.
Colla[modifica | modifica wikitesto]
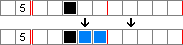
A volte è presente una cella piena la cui distanza dal bordo è minore dell'indizio. In questo caso l'indizio si propaga dalla cella piena in direzione opposta rispetto al bordo.
Per esempio, se si ha una riga di 10 celle la cui terza casella è piena e si ha l'indizio "5", l'indizio si propaga fino alla quinta cella.
Questo metodo si può utilizzare anche lontano dai bordi.

- Uno spazio si comporta come un bordo se l'indizio è forzato a destra dello spazio.
- Il primo indizio può essere preceduto da altri indizi se essi sono già fissati alla sinistra dello spazio usato come bordo,
Libri[modifica | modifica wikitesto]
Diversi libri sul nonogram sono stati pubblicati negli Stati Uniti d'America dal 2006 a causa del successo avuto l'anno prima da un altro gioco, il Sudoku. I titoli comprendono Paint-doku, O'ekaki: Paint by Sudoku, The Essential Book of Hanjie e Crosspix.
Voci correlate[modifica | modifica wikitesto]
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file su nonogram
Wikimedia Commons contiene immagini o altri file su nonogram