Biforcazione a nodo sella
In Matematica, una biforcazione a nodo sella è una biforcazione locale nella quale, al variare del parametro, si ha la creazione o la distruzione dei punti d'equilibrio. L'esempio classico di nodo sella è dato dall'equazione differenziale
dove r è il parametro che può assumere valori positivi, negativi o nulli.
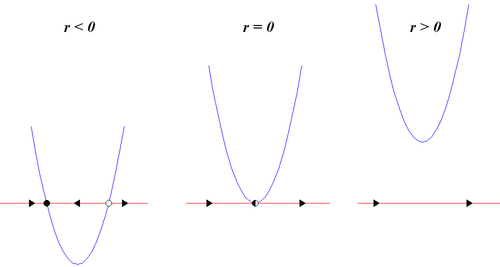
- Se vi sono due punti d'equilibrio, uno stabile a ed uno instabile a .
- Quando (punto di biforcazione) vi è esattamente un punto fisso. Tale punto (non più iperbolico) è chiamato punto sella ed è originato dal collasso in un unico punto dei due punti d'equilibrio visti prima. Per tale ragione conserva a sinistra le caratteristiche di stabilità e a destra quelle di instabilità.
- Se i punti di equilibrio scompaiono.
Dal diagramma di biforcazione si vede che tutti i punti di equilibiro sono instabili
Un altro esempio di biforcazione a sella è dato dall'equazione differenziale:
In tal caso si ottengono risultati speculari a quanto visto sopra rispetto al valore critico ovvero:
- nessuno punto di equilibrio per ;
- un punto d'equilibrio semistabile (instabile a destra e stabile a sinistra«») in per ;
- due punti di equilibrio per , di cui: uno instabile in ed uno stabile in .
Anche il diagramma di biforcazione risulta speculare al diagramma della prima forma rispetto al punto .
Le due parabole sono dette forme canoniche o forme normali delle biforcazioni a nodo sella, in quanto ogni altra biforcazione dello stesso tipo può essere ricondotta qualitativamente ad una delle due. Inoltre anche altri tipi di sistemi si possono studiare, in determinati intervalli, come fossero nodi sella.
Terminologia[modifica | modifica wikitesto]
La biforcazione a nodo sella (saddle-node in inglese) è detta anche biforcazione tangente (tangential bifurcation) o biforcazione fold (da fold, piega). A causa dell'improvvisa apparizione e scomparsa dei punti d'equilibrio per parametri ai due lati del valore critico, Ralph Abraham ha inventato il nome di blue sky bifurcation (dall'espressione inglese out of the clear blue sky = improvvisamente, senza segnali d'avvertimento).
Un caso pratico[modifica | modifica wikitesto]
Tramite la biforcazione nodo sella è possibile descrivere il bloccaggio degli pneumatici durante una frenata di emergenza, infatti la curva che caratterizza l'aderenza di uno pneumatico ha un andamento di tipo quadratico. Quando si applica una coppia frenante alla ruota, nascono due equilibri di cui solo uno stabile, gli equilibri si avvicinano all'aumentare della coppia frenante fino a collidere e dare luogo ad un equilibrio di sella. Il valore di coppia frenante per cui avviene tale fenomeno è il massimo applicabile, oltre il quale entrambi gli equilibri scompaiono e la ruota tende al bloccaggio.
Transizione al caos[modifica | modifica wikitesto]
La transizione al caos del sistema si ha quando il sistema raggiunge il valore critico del parametro di controllo del sistema. Il tipo di transizione al caos del tipo di sistemi come quello "Saddle-Node" è definito come meccanismo di intermittenza ed è stato teorizzato da Pomeau e Manneville nel 1980. Quello che si nota in questo tipo di sistemi è, superato il parametro critico, si hanno dei "burst" caotici che compaiono all'interno del comportamento regolare. La durata degli intervalli regolari, nell'intorno del valore critico del parametro, va come 1/(r-rc) dove r è il valore del parametro e rc è il valore critico dopo il quale si hanno i burst caotici. In un diagramma di biforcazione quello che si vede è che il punto fisso stabile e quello instabile si avvicinano all'approssimarsi del valore critico del parametro fino a fondersi al valore critico e a scomparire appena dopo.
Bibliografia[modifica | modifica wikitesto]
- Strogatz S.H. (1994), Nonlinear Dynamics and Chaos (Perseus Books, Cambridge)
- Cencini M., Cecconi F., Vulpiani A. (2010), "Chaos" (World Scientific)
Voci correlate[modifica | modifica wikitesto]
- Biforcazione a forcone
- Biforcazione transcritica
- Diagrammi di biforcazione
- Larva del pino (sistema dinamico)
- Teoria delle biforcazioni
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file su Biforcazione a nodo sella
Wikimedia Commons contiene immagini o altri file su Biforcazione a nodo sella












