Biforcazione imperfetta
In matematica, una biforcazione è detta imperfetta se il suo studio è riconducibile a quello di una biforcazione canonica a meno di un fattore di disturbo.
Un esempio è dato dall'equazione differenziale della biforcazione pitchfork cui viene aggiunta, come imperfezione, una costante :
Se si perde la simmetria classica dei sistemi con biforcazioni a forcone. Per tale ragione è detto parametro di imperfezione.
Studio della funzione[modifica | modifica wikitesto]
L'equazione differenziale è di difficile studio analitico, poiché vi sono due diversi parametri che fanno variare il sistema (ossia ed ).
Per ovviare a tale problema si considerano vari grafici con fissato e si studia geometricamente il sistema al variare del parametro . In particolare si cercano le intersezioni tra le curve ed .
Caso [modifica | modifica wikitesto]
Quando la cubica è monotòna non crescente. La linea orizzontale si interseca con la cubica esattamente in un punto per ogni valore di .
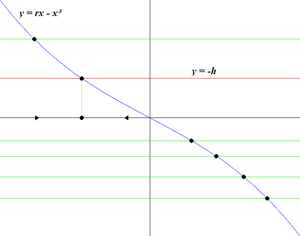
Caso [modifica | modifica wikitesto]
Quando la curva non è più monotòna, quindi al variare di vi sono una, due o tre intersezioni.
Poiché lo studio delle intersezioni è simmetrico rispetto ad , studiamo i vari casi solo per (ovvero ).
Vi sarà un valore critico del parametro, , in cui la linea orizzontale è esattamente la tangente alla curva . Tale valore sarà dato dal massimo (minimo nel lato simmetrico rispetto all'asse delle ascisse) relativo alla cubica.
Per ricavare il valore del massimo e quello di studiamo la derivata
da cui, scegliendo il valore positivo:
e quindi:

Vediamo che succede diminuendo il parametro :
- per si ha una sola intersezione che corrisponde ad un punto d'equilibrio stabile (la stabilità è facilmente ricavabile sia analiticamente sia geometricamente);
- per nasce un nuovo punto d'equilibrio semistabile (instabile a sinistra e stabile a destra) che si aggiunge al punto d'equilibrio stabile già presente;
- per vi sono, oltre al primo punto fisso stabile, due punti d'equilibrio distinti: uno più centrale rispetto alla simmetria della cubica instabile e l'altro stabile.
Ovviamente una situazione speculare la si verifica per .
Per i valori critici ed vi è l'improvvisa comparsa/scomparsa di due punti d'equilibrio, ovvero si ha, localmente, una biforcazione saddle-node.
Diagramma di biforcazione vs. [modifica | modifica wikitesto]

Studiando la stabilità tramite diagramma di biforcazione si vede che, se si ha il diagramma solito della biforcazione pitchfork, mentre per si ottengono due curve disgiunte:
- un ramo stabile definito per ogni , che tende a per e a per ;
- una curva definita per composta da un ramo stabile ed uno instabile che per tendono rispettivamente a (in segno opposto al ramo stabile precedente) e a .
Bibliografia[modifica | modifica wikitesto]
- Strogatz S.H. (1994), Nonlinear Dynamics and Chaos (Perseus Books, Cambridge).




























