Utente:Grasso Luigi/sandbox2/Teorema di rotazione di Eulero

In geometria, il teorema della rotazione di Eulero afferma che, in uno spazio 3-dimensionale, qualsiasi spostamento di un corpo rigido con un punto del corpo fisso nel riferimento, equivale ad una rotazione singola su un asse che attraversa il punto fissato. Ciò significa in altre parole che componendo due rotazioni si ottiene ancora una rotazione. Quindo l'insieme delle rotazioni ha la struttura di un gruppo, detto gruppo rotazione SO(3).
Il teorema prende il nome da Leonhard Euler, che lo provò per primo nel 1775 tramite la geometria sferica. L'asse di rotazione è noto come un asse di Eulero, tipicamente rappresentato da un vettore unità . Il suo prodotto con l'angolo di rotazione viene detto asse angolo. L'estensione del teorema alla cinematica introduce il concetto di asse istantaneo di rotazione, una linea di punti fissi.
In termini di algebra lineare, il teorema afferma che, nello spazio 3D, due sistemi di coordinate cartesiani con un'origine comune sono correlati da una rotazione attorno ad un asse fisso. In altri termini il prodotto di due matrici di rotazione è ancora una matrice di rotazione e per una matrice di rotazione non unitaria, un autovalore è reale con valore 1 e gli altri due o sono complessi coniugati, o reali coincidenti al valore −1. L'autovettore corrispondente all'autovalore è l'asse di rotazione che connette i due sistemi.
Teorema di Eulero (1776)[modifica | modifica wikitesto]
Eulero enuncia il teorema come segue: [1]
Theorema. Quomodocunque sphaera circa centrum suum conuertatur, semper assignari potest diameter, cuius directio in situ translato conueniat cum situ initiali.
o (in Italiano):
Teorema. Quando una sfera viene mossa attorno al suo centro, è sempre possibile trovare un diametro la cui direzione è nella posizione spostata lo stesso come nella posizione iniziale.

Dimostrazione[modifica | modifica wikitesto]
La dimostrazione originale di Eulero utilizza la geometria sferica e quindi ogni volta che si parla di triangoli devono essere intesi come triangoli sferici.
Analisi iniziale di Eulero[modifica | modifica wikitesto]
Per arrivare alla dimostrazione, Eulero analizza come sarebbe la situazione se il teorema fosse vero. A tal fine, supponiamo che la linea gialla in figura 1 passa per il centro della sfera ed è l'asse di rotazione che stiamo cercando, e il punto è uno dei due punti d'intersezione di quell'asse con la sfera. Allora considera un cerchio arbitrario che non contiene (il cerchio blu), e la sua immagine dopo la rotazione (il cerchio rosso), che è ancora un cerchio che non contiene . Contrassegna un punto sulla loro intersezione con . (Se i cerchi coincidono, allora può essere un qualsiasi punto su entrambi; altrimenti è uno dei due punti d'intersezione.)

Adesso sta sul cerchio iniziale (blu), e la sua immagine sarà sul cerchio trasportato (rosso). Denotiamo tale punto immagine con . Poichè sta pure sul cerchio ruotato (rosso), è l'immagine di un punto che sta sul cerchio iniziale (blu) e denota tale preimmagine con (vedi la figura 2). Allora considera i due archi di congiunzione e . Essi hanno la stessa lunghezza perchè l'arco si trasforma nell'arco . Inoltre, poiché è un punto fissato, il triangolo si trasforma nel triangolo , questi sono triangoli isosceli, e l'arco biseca l'angolo ∠ (arco bisettrice simile alla retta bisettrice della geometria ordinaria).
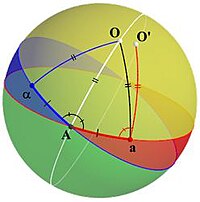
Costruzione del meglio punto invariante[modifica | modifica wikitesto]
Costruiamo un punto che potrebbe essere invariante utilizzando le considerazioni precedenti. Iniziamo con il cerchio blu e la sua immagine sotto la trasformazione di rotazione attorno al diametro della sfera per , che è il cerchio rosso come nella figura 1. Sia un punto intersezione dei due cerchi. Se l'immagine di sotto trasformazione è lo stesso punto allora è un punto fisso della trasformazione, e dato che il centro è anche un punto fisso, il diametro della sfera contenente è l'asse di rotazione e questo prova il teorema.
Nel caso in cui è l'immagine di e la sua preimmagine, allora connettiamo questi due punti ad con gli archi e . Questi archi hanno la stessa lunghezza. Costriamo il cerchio che biseca ∠ e individuiamo il punto sul cerchio in maniera tale che gli archi e hanno stessa lunghezza, e denotiamo la regione della sfera contenente e limitata dai cerchi blu e rosso l'interno dell'angolo sferico ∠ . (Quella regione gialla in figure 3.) Essendo = e inoltre è sull'arco bisettrice dell'angolo sferico ∠ , noi allora abbiamo che = .
Dimostrazione invarianza per trasformazioni geometriche[modifica | modifica wikitesto]
Adesso supponiamo che ' sia l'immagine di . Allora noi sappiamo che ∠ = ∠' e l'orientazione è preservata,[note 1] così deve essere interno a ∠. Ora si trasforma in ', così = '. Dato che è di lunghezza uguale a , ∠ = ∠. Ma ∠ = ∠', cioè ∠ = ∠' e quindi ' e sono gli stessi punti. In altre parole, è un punto fisso della trasformazione, ed essendo pure il centro un punto fisso, il diametro della sfera contenente è l'asse di rotazione.
Note finali sulla costruzione[modifica | modifica wikitesto]

Eulero fa notare che il punto si trova intersecando il the perpendicular bisector dell'arco con l'angolo bisector of Template:Math, una costruzione che potrebbe essere più facile nella pratica. Inoltre l'asse di rotazione si trova intersecando i seguenti due piani:
- il piano di simmetria dell'angolo ∠ (che passa per il centro della sfera), e
- il piano di simmetria dell'arco (che passa anche per ).
- Proposizione. I due piani intersecano in un diametro. Questo diametro è quello che stiamo cercando.
- Dimostrazione. Sia uno dei due estremi (ce ne sono due) di questo diametro sulla superficie della sfera. Essendo trasformato in e i triangoli hanno stessi angoli, ne segue che il triangolo viene trasportato sul triangolo . Qundi il punto rimane fisso durante il movimento.
- Corollari. Questo mostra anche che la rotazione della sfera può essere vista come due riflessioni consecutive sui due piani descritti sopra. I punti in un piano speculare sono invarianti per riflessione, e quindi i punti sulla loro intersezione (una linea: l'asse della rotazione) sono invarianti per entrambe le riflessioni, e quindi per rotazione.
Un'altra maniera semplice per trovare l'asse di rotazione è quello di considerare il piano contenente i punti , e . L'asse di rotazione è ovviamente ortogonale a questo piano e passa per il centro della sfera.
Dato che per un corpo rigido un qualsiasi movimento che lasci invariante un asse è una rotazione, questo dimostra anche che una qualsiasi arbitraria composizione delle rotazioni equivale a una singola rotazione attorno a un nuovo asse.
Uso delle matrici[modifica | modifica wikitesto]
Una rotazione spaziale è una trasformazione lineare biunivoca rappresentata da una matrice di rotazione 3 × 3 che trasforma le coordinate di un vettore nelle coordinate , cioè = . Quindi, un'altra versione del teorema di Eulero è che per ogni rotazione , esiste un vettore non nullo per cui = ; ciò equivale a dire che è un autovettore di associato all'autovalore 1. Quindi è sufficiente provare che 1 è un autovalore di ; l'asse di rotazione di sarà la linea , dove è l'autovettore con autovalore 1.
A rotation matrix has the fundamental property that its inverse is its transpose, that is
where Template:Math is the 3 × 3 identity matrix and superscript T indicates the transposed matrix.
Compute the determinant of this relation to find that a rotation matrix has determinant ±1. In particular,
A rotation matrix with determinant +1 is a proper rotation, and one with a negative determinant −1 is an improper rotation, that is a reflection combined with a proper rotation.
It will now be shown that a rotation matrix Template:Math has at least one invariant vector Template:Math, i.e., Template:Math. Because this requires that Template:Math, we see that the vector Template:Math must be an eigenvector of the matrix Template:Math with eigenvalue Template:Math. Thus, this is equivalent to showing that Template:Math.
Use the two relations
for any 3 × 3 matrix A and
(since Template:Math) to compute
This shows that Template:Math is a root (solution) of the characteristic equation, that is,
In other words, the matrix Template:Math is singular and has a non-zero kernel, that is, there is at least one non-zero vector, say Template:Math, for which
The line Template:Math for real Template:Mvar is invariant under Template:Math, i.e., Template:Math is a rotation axis. This proves Euler's theorem.
Equivalence of an orthogonal matrix to a rotation matrix[modifica | modifica wikitesto]
Two matrices (representing linear maps) are said to be equivalent if there is a change of basis that makes one equal to the other. A proper orthogonal matrix is always equivalent (in this sense) to either the following matrix or to its vertical reflection:
Then, any orthogonal matrix is either a rotation or an improper rotation. A general orthogonal matrix has only one real eigenvalue, either +1 or −1. When it is +1 the matrix is a rotation. When −1, the matrix is an improper rotation.
If Template:Math has more than one invariant vector then Template:Math and Template:Math. Any vector is an invariant vector of Template:Math.
Richiami sulla teoria delle matrici[modifica | modifica wikitesto]
In order to prove the previous equation some facts from matrix theory must be recalled.
An Template:Math matrix Template:Math has Template:Math orthogonal eigenvectors if and only if Template:Math is normal, that is, if Template:Math.[N 1] This result is equivalent to stating that normal matrices can be brought to diagonal form by a unitary similarity transformation:
and Template:Math is unitary, that is,
The eigenvalues Template:Math are roots of the characteristic equation. If the matrix Template:Math happens to be unitary (and note that unitary matrices are normal), then
and it follows that the eigenvalues of a unitary matrix are on the unit circle in the complex plane:
Also an orthogonal (real unitary) matrix has eigenvalues on the unit circle in the complex plane. Moreover, since its characteristic equation (an Template:Mvarth order polynomial in Template:Mvar) has real coefficients, it follows that its roots appear in complex conjugate pairs, that is, if Template:Mvar is a root then so is Template:Math. There are 3 roots, thus at least one of them must be purely real (+1 or −1).
After recollection of these general facts from matrix theory, we return to the rotation matrix Template:Math. It follows from its realness and orthogonality that we can find a Template:Math such that:
If a matrix Template:Math can be found that gives the above form, and there is only one purely real component and it is −1, then we define R to be an improper rotation. Let us only consider the case, then, of matrices R that are proper rotations (the third eigenvalue is just 1). The third column of the 3 × 3 matrix Template:Math will then be equal to the invariant vector Template:Math. Writing Template:Math and Template:Math for the first two columns of Template:Math, this equation gives
If Template:Math has eigenvalue 1, then Template:Math and Template:Math has also eigenvalue 1, which implies that in that case Template:Math.
Finally, the matrix equation is transformed by means of a unitary matrix,
which gives
The columns of Template:Math are orthonormal. The third column is still Template:Math, the other two columns are perpendicular to Template:Math. We can now see how our definition of improper rotation corresponds with the geometric interpretation: an improper rotation is a rotation around an axis (here, the axis corresponding to the third coordinate) and a reflection on a plane perpendicular to that axis. If we only restrict ourselves to matrices with determinant 1, we can thus see that they must be proper rotations. This result implies that any orthogonal matrix Template:Math corresponding to a proper rotation is equivalent to a rotation over an angle Template:Mvar around an axis Template:Math.
Classi di equivalenza[modifica | modifica wikitesto]
The trace (sum of diagonal elements) of the real rotation matrix given above is Template:Math. Since a trace is invariant under an orthogonal matrix similarity transformation,
it follows that all matrices that are equivalent to Template:Math by such orthogonal matrix transformations have the same trace: the trace is a class function. This matrix transformation is clearly an equivalence relation, that is, all such equivalent matrices form an equivalence class.
In fact, all proper rotation 3 × 3 rotation matrices form a group, usually denoted by SO(3) (the special orthogonal group in 3 dimensions) and all matrices with the same trace form an equivalence class in this group. All elements of such an equivalence class share their rotation angle, but all rotations are around different axes. If Template:Math is an eigenvector of Template:Math with eigenvalue 1, then Template:Math is also an eigenvector of Template:MathT, also with eigenvalue 1. Unless Template:Math, Template:Math and Template:Math are different.
Applicazioni[modifica | modifica wikitesto]
Generatori delle rotazioni[modifica | modifica wikitesto]
Suppose we specify an axis of rotation by a unit vector Template:Math, and suppose we have an infinitely small rotation of angle Template:Math about that vector. Expanding the rotation matrix as an infinite addition, and taking the first order approach, the rotation matrix Template:Math is represented as:
A finite rotation through angle Template:Mvar about this axis may be seen as a succession of small rotations about the same axis. Approximating Template:Math as Template:Math where Template:Math is a large number, a rotation of Template:Mvar about the axis may be represented as:
It can be seen that Euler's theorem essentially states that all rotations may be represented in this form. The product Template:Math is the "generator" of the particular rotation, being the vector Template:Math associated with the matrix Template:Math. This shows that the rotation matrix and the axis–angle format are related by the exponential function.
One can derive a simple expression for the generator Template:Math. One starts with an arbitrary plane (in Euclidean space) defined by a pair of perpendicular unit vectors Template:Math and Template:Math. In this plane one can choose an arbitrary vector Template:Math with perpendicular Template:Math. One then solves for Template:Math in terms of Template:Math and substituting into an expression for a rotation in a plane yields the rotation matrix Template:Math which includes the generator Template:MathTTemplate:MathT.
To include vectors outside the plane in the rotation one needs to modify the above expression for Template:Math by including two projection operators that partition the space. This modified rotation matrix can be rewritten as an exponential function.
Analysis is often easier in terms of these generators, rather than the full rotation matrix. Analysis in terms of the generators is known as the Lie algebra of the rotation group.
Quaternioni[modifica | modifica wikitesto]
It follows from Euler's theorem that the relative orientation of any pair of coordinate systems may be specified by a set of three independent numbers. Sometimes a redundant fourth number is added to simplify operations with quaternion algebra. Three of these numbers are the direction cosines that orient the eigenvector. The fourth is the angle about the eigenvector that separates the two sets of coordinates. Such a set of four numbers is called a quaternion.
While the quaternion as described above, does not involve complex numbers, if quaternions are used to describe two successive rotations, they must be combined using the non-commutative quaternion algebra derived by William Rowan Hamilton through the use of imaginary numbers.
Rotation calculation via quaternions has come to replace the use of direction cosines in aerospace applications through their reduction of the required calculations, and their ability to minimize round-off errors. Also, in computer graphics the ability to perform spherical interpolation between quaternions with relative ease is of value.
Generalizzazioni[modifica | modifica wikitesto]

In higher dimensions, any rigid motion that preserve a point in dimension Template:Math or Template:Math is a composition of at most Template:Mvar rotations in orthogonal planes of rotation, though these planes need not be uniquely determined, and a rigid motion may fix multiple axes.
A rigid motion in three dimensions that does not necessarily fix a point is a "screw motion". This is because a composition of a rotation with a translation perpendicular to the axis is a rotation about a parallel axis, while composition with a translation parallel to the axis yields a screw motion; see screw axis. This gives rise to screw theory.
Note[modifica | modifica wikitesto]
Riferimenti
- ^ Novi Commentarii academiae scientiarum Petropolitanae 20, 1776, pp. 189–207 (E478)
Postille
- ^ L'orientazione si preserva nel senso che se viene ruotato attorno nel senso antiorario per allinearsi con , allora dev'essere ruotato attorno in senso antiorario per allinerasi con . In maniera simile per le rotazioni orarie.
Bibliografia[modifica | modifica wikitesto]
- A Disorienting Look at Euler's Theorem on the Axis of a Rotation, in American Mathematical Monthly, vol. 116, n. 10, 2009, pp. 892–909, DOI:10.4169/000298909x477014.
- Euler's theorem and its proof are contained in paragraphs 24–26 of the appendix (Additamentum. pp. 201–203) of L. Eulero (Leonhard Euler), Formulae generales pro translatione quacunque corporum rigidorum (General formulas for the translation of arbitrary rigid bodies), presented to the St. Petersburg Academy on October 9, 1775, and first published in Novi Commentarii academiae scientiarum Petropolitanae 20, 1776, pp. 189–207 (E478) and was reprinted in Theoria motus corporum rigidorum, ed. nova, 1790, pp. 449–460 (E478a) and later in his collected works Opera Omnia, Series 2, Volume 9, pp. 84–98.
Voci correlate[modifica | modifica wikitesto]
- Ancgoli di Eulero
- Parametri di Eulero–Rodrigues
- Formalismi delle rotazioni in tre dimensioni
- Operatore rotazione
- Velocità angolare
- Rotazione con un asse fisso
- Matrice esponenziale
- Rappresentazione asse–angolo
Collegamenti esterni[modifica | modifica wikitesto]
- Euler's original treatise in The Euler Archive: entry on E478, first publication 1776 pdf)
- Euler's original text (in Latin) and English translation (by Johan Sten)
- Wolfram Demonstrations Project for Euler's Rotation Theorem (by Tom Verhoeff)
Errore nelle note: Sono presenti dei marcatori <ref> per un gruppo chiamato "N" ma non è stato trovato alcun marcatore <references group="N"/> corrispondente










































![{\displaystyle \mathrm {Tr} \left[\mathbf {A} \mathbf {R} \mathbf {A} ^{\mathsf {T}}\right]=\mathrm {Tr} \left[\mathbf {R} \mathbf {A} ^{\mathsf {T}}\mathbf {A} \right]=\mathrm {Tr} [\mathbf {R} ]\quad {\text{ with }}\quad \mathbf {A} ^{\mathsf {T}}=\mathbf {A} ^{-1},}](https://wikimedia.org/api/rest_v1/media/math/render/svg/899635016524f868479646782fb830845ff74608)


![{\displaystyle {\begin{aligned}\mathbf {x} &=\mathbf {a} \cos \alpha +\mathbf {b} \sin \alpha \\\mathbf {y} &=-\mathbf {a} \sin \alpha +\mathbf {b} \cos \alpha \\\cos \alpha &=\mathbf {a} ^{\mathsf {T}}\mathbf {x} \\\sin \alpha &=\mathbf {b} ^{\mathsf {T}}\mathbf {x} \\[8px]\mathbf {y} &=-\mathbf {ab} ^{\mathsf {T}}\mathbf {x} +\mathbf {ba} ^{\mathsf {T}}\mathbf {x} =\left(\mathbf {ba} ^{\mathsf {T}}-\mathbf {ab} ^{\mathsf {T}}\right)\mathbf {x} \\[8px]\mathbf {x} '&=\mathbf {x} \cos \beta +\mathbf {y} \sin \beta \\&=\left(\mathbf {I} \cos \beta +\left(\mathbf {ba} ^{\mathsf {T}}-\mathbf {ab} ^{\mathsf {T}}\right)\sin \beta \right)\mathbf {x} \\[8px]\mathbf {R} &=\mathbf {I} \cos \beta +\left(\mathbf {ba} ^{\mathsf {T}}-\mathbf {ab} ^{\mathsf {T}}\right)\sin \beta \\&=\mathbf {I} \cos \beta +\mathbf {G} \sin \beta \\[8px]\mathbf {G} &=\mathbf {ba} ^{\mathsf {T}}-\mathbf {ab} ^{\mathsf {T}}\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d175427ea3f50e3a47d46efa881390700db86f6e)


