Problema di Lambert
In meccanica celeste, il problema di Lambert riguarda la determinazione di un'orbita partendo da due vettori di posizione e dal tempo di volo. È stato risolto dal matematico svizzero Johann Heinrich Lambert. Ha importanti applicazioni nell'ambito dei rendezvous e delle manovre orbitali.
Si supponga che un corpo, sotto l'influenza di una forza gravitazionale, venga osservato mentre si sposta da un punto P1 fino al punto P2, lungo una determinata traiettoria conica, in un tempo T. In tale ipotesi, il teorema di Lambert afferma che il tempo di volo dipende da alcuni parametri geometrici del problema. Più precisamente, l'enunciato del teorema è il seguente:
«Il tempo necessario a un corpo per spostarsi tra due punti di una traiettoria conica è funzione solamente della somma delle distanze dei due punti dall'origine della forza, della distanza lineare tra i due punti e dal semiasse maggiore della conica.»
Espresso in un altro modo, il problema di Lambert può essere formulato imponendo determinate condizioni al contorno all'equazione differenziale del problema dei due corpi
- ,
per la quale l'orbita kepleriana è la soluzione generale.
Formulazione esatta[modifica | modifica wikitesto]
La formulazione precisa del problema di Lambert è la seguente.
Sono dati due differenti momenti temporali e e due vettori di posizione e .
Trovare la soluzione che soddisfa l'equazione differenziale di prima per cui
- .
Analisi geometrica preliminare[modifica | modifica wikitesto]

, l'origine della forza gravitazionale;
, il punto corrispondente al vettore ;
, il punto corrispondente al vettore .
I tre punti
, origine della forza gravitazionale,
, punto corrispondente al vettore ,
, punto corrispondente al vettore ,
formano un triangolo nel piano definito dai vettori e e rappresentato nella figura 1. La distanza tra i punti e è , la distanza tra e è e la distanza tra e è . Il valore di è positivo o negativo a seconda di quale tra i punti e sia più distante da . Il problema geometrico da risolvere è di trovare un'ellisse che attraversi i punti e e abbia un fuoco in .
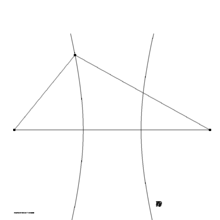
I punti , e definiscono un'iperbole che attraversa il punto e ha i fuochi nei punti e , come mostrato in figura 2. Il punto può trovarsi o sul ramo destro o su quello sinistro dell'iperbole, a seconda del segno di . Il semiasse maggiore dell'iperbole è e l'eccentricità è .
L'equazione dell'iperbole, in coordinate cartesiane, è
con
Per ogni punto sullo stesso ramo dell'iperbole a cui appartiene la differenza tra le distanze dai punti e è
Per ogni punto sull'altro ramo dell'iperbole la relazione corrispondente è
cioè

Questo significa che i punti e appartengono entrambi all'ellisse che ha come fuochi i punti e e semiasse maggiore
L'ellisse risultante, scelto un punto arbitrario, è mostrato nella figura 3.
Soluzione del problema di Lambert per un'orbita ellittica[modifica | modifica wikitesto]
Prima di tutto si considerano due casi separati a seconda che il polo orbitale abbia direzione oppure . Nel primo caso l'angolo di trasferimento per il primo passaggio attraverso sarà compreso nell'intervallo , mentre nel secondo caso sarà compreso nell'intervallo . Quindi continuerà a passare attraverso ad ogni rivoluzione orbitale.
Nel caso in cui , come ad esempio nel caso in cui e abbiano direzione opposta, tutti i piani orbitali che contengono la linea corrispondente sono ugualmente adatti e l'angolo di trasferimento per il primo passaggio attraverso sarà di .
Per ogni per cui sia , nel triangolo formato dai punti , e , come mostrato in figura 1, si ha
e il semiasse maggiore (con segno) dell'iperbole è
L'eccentricità (con segno) dell'iperbole è
e il semiasse minore è
Le coordinate del punto relative al sistema di coordinate canoniche per l'iperbole sono
(notare che ha il segno di )
dove
Scegliendo la coordinata y del punto sull'altro ramo dell'iperbole come parametro libero, la coordinata x di è
(notare che ha il segno di )
Il semiasse maggiore dell'ellisse passante per i punti e e avente i fuochi nei punti e è
La distanza tra i fuochi è
e l'eccentricità è di conseguenza
L'anomalia vera nel punto dipende dalla direzione del moto, ovvero dal segno di . In entrambi i casi si ha che
dove
è il versore che rappresenta la direzione da a espresso in coordinate canoniche.
Se è positivo, allora
Se è negativo, invece
Essendo
- il semiasse maggiore ,
- l'eccentricità orbitale ,
- l'anomalia vera iniziale
funzioni note del parametro y, il tempo necessario all'anomalia vera per aumentare di un valore è anch'esso una funzione nota di y. Se è nell'intervallo che si può ottenere con un'orbita kepleriana ellittica, il valore di y corrispondente può essere ottenuto con un algoritmo iterativo.
Nel caso particolare che si abbia (o molto simili), si ha che e l'iperbole si riduce ad un'unica linea ortogonale alla congiungente di con con equazione
Le equazioni (11) e (12) sono quindi sostituite con
la (14) è sostituita con
e la (15) con
Esempio numerico[modifica | modifica wikitesto]
Si assumano i seguenti valori per un'orbita kepleriana centrata sulla Terra:
- r1 = 10 000 km
- r2 = 10 000 km
- α = 100°
Scegliendo un valore di y = 30 000 km, si ottiene un tempo di trasferimento di 3072 secondi, assumendo la costante gravitazionale uguale a μ = 398 603 km3/s2. I corrispondenti parametri orbitali sono:
- semiasse maggiore = 23 001 km;
- eccentricità = 0,566613;
- anomalia vera al tempo t1 = -7,577°;
- anomalia vera al tempo t2 = 92,423°.
Ponendo invece:
- r1 = 10 000 km
- r2 = 10 000 km
- α = 260°
si ottiene la stessa orbita ellittica, ma la rotazione avviene nella direzione opposta e si ha:
- anomalia vera al tempo t1 = 7,577°;
- anomalia vera al tempo t2 = 267,577° = 360° - 92,423°
e un tempo di trasferimento di 31 645 secondi.
Le componenti radiale e tangenziale della velocità sono date da:
Applicazioni pratiche[modifica | modifica wikitesto]
Normalmente questo algoritmo viene utilizzato per risolvere il problema di Lambert nella progettazione di missioni interplanetarie. Ad esempio, un veicolo spaziale che si sposti dalla Terra verso Marte può essere considerato in prima approssimazione su di un'orbita kepleriana ellittica eliocentrica dalla posizione della Terra al momento del lancio alla posizione di Marte al momento dell'arrivo. Confrontando i vettori delle velocità iniziale e finale per la Terra e Marte si può ottenere una buona stima dell'energia di lancio richiesta e delle manovre necessarie per l'inserimento nell'orbita marziana.
Voci correlate[modifica | modifica wikitesto]
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) Codice MATLAB per la risoluzione del problema di Lambert, su mathworks.com.


































































