Figura di Lissajous

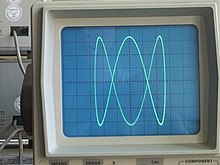
Figura di Lissajous su un oscilloscopio

Figura di Lissajous in tre dimensioni

In matematica e in fisica per figura di Lissajous si intende il grafico di una curva data dal sistema di equazioni parametriche

$x = A_x\cos(\omega_x t+\phi_x),\quad y = A_y\sin(\omega_y t + \phi_y),$

dove le A_i sono le ampiezze, le ω_i le pulsazioni e le φ_i le fasi di due moti oscillatori ortogonali.

Esse sono state ampiamente studiate dal fisico Jean Antoine Lissajous (1822 - 1880). In precedenza, nell'anno 1815, erano state studiate dall'astronomo americano Nathaniel Bowditch (1773 - 1838) e sono chiamate anche figure di Bowditch.

L'aspetto di queste figure è molto sensibile al rapporto $\frac{\omega_x}{\omega_y}$ .

In particolare, quando tale rapporto è pari ad uno, la figura risulta essere, in generale, un'ellisse, che diventa una circonferenza nel caso in cui sia anche $A_x=A_y$ , $\phi_x=0$ e $\phi_y=0$ (moti oscillatori tra loro in quadratura), e si riduce ad un segmento nel caso in cui sia anche $\phi_x=-\frac{\pi}{2}$ , $\phi_y=0$ (moti oscillatori tra loro in fase). Un'altra semplice figura di Lissajous è la parabola, che si ottiene quando $\frac{\omega_x}{\omega_y}=2$ e $\phi_x=0$ , $\phi_y=0$ . Altri rapporti producono curve più complicate, che sono chiuse solo se il rapporto $\frac{\omega_x}{\omega_y}$ è razionale. La forma di queste curve spesso ricorda un nodo tridimensionale, e in effetti molti tipi di nodi, quando vengono proiettati su un piano, diventano figure di Lissajous.