Rapporto di onda stazionaria
In una linea di trasmissione, il VSWR (Voltage Standing Wave Ratio) o ROS (Rapporto di Onda Stazionaria) è un parametro che indica il rapporto tra il valore massimo e il valore minimo del modulo della tensione lungo la linea.
Fissata una certa frequenza, il ROS è una misura del disadattamento di impedenza tra la linea di trasmissione ed il suo carico. Maggiore è il ROS, maggiore è il disadattamento. Il valore minimo del ROS, che corrisponde alla condizione di perfetto adattamento per cui le impedenze della linea di trasmissione e del carico sono uguali con assenza di onda riflessa, è pari a 1. Valori finiti maggiori di 1 indicano disadattamento con presenza di un'onda stazionaria dovuta a riflessione parziale dal carico. Se il ROS è pari a è presente solo un'onda stazionaria dovuta a riflessione totale dal carico, per cui onda diretta e onda riflessa hanno la stessa ampiezza.
Premesse matematiche e definizione di coefficiente di riflessione
[modifica | modifica wikitesto]Come è noto, indicate, rispettivamente, con V(x,t) e I(x.t) la tensione e la corrente in una certa posizione x lungo una linea di trasmissione e in un certo istante t, esse soddisfano le equazioni dei telegrafisti:
- (1)
- (2)
dove, R, L, G, C sono, rispettivamente, la resistenza e l'induttanza per unità di lunghezza dei due conduttori che compongono la linea, la conduttanza e la capacità per unità di lunghezza tra gli stessi due conduttori.
Nel caso in cui sia fissata la frequenza con un generatore di onda sinusoidale, anche la tensione e la corrente in una generica posizione x hanno andamento sinusoidale e, applicando il metodo simbolico, si può scrivere:
- con
- con
dove j è l'unità immaginaria e è la frequenza angolare o pulsazione, tenendo presente che
- ha significato fisico solo la parte reale delle grandezze complesse così introdotte,
- eventuali fasi iniziali e, in generale, termini additivi costanti presenti all'esponente di ciascun esponenziale complesso vengono inclusi nei termini complessi e .
In tal caso, è possibile dimostrare che dalle equazioni dei telegrafisti si ha:[1]
- (3)
- (4)
dove
è la cosiddetta costante di propagazione e dove ed sono, rispettivamente, l'impedenza per unità di lunghezza e l'ammettenza per unità di lunghezza della linea.
La soluzione generale delle equazioni (3) e (4) è:
- (5)
- (6)
dove
- è un numero complesso che nel caso di linee non dissipative (R=0, G=0) si riduce all'impedenza caratteristica
e dove
- in cui è detta costante di attenuazione e costante di fase.
Soffermiamoci sull'andamento della tensione. Dalla (5), si evince che la soluzione più generale si esprime come somma di due termini:
- che rappresenta un'onda progressiva
- che rappresenta un'onda regressiva.
Si definisce, inoltre, coefficiente di riflessione in un generico punto di una linea di trasmissione il rapporto tra l'onda di tensione regressiva e quella progressiva. Se l'onda regressiva è generata da una riflessione che avviene per la presenza di un carico a fine linea, si dice anche che il coefficiente di riflessione è definito come il rapporto tra l'onda di tensione riflessa e quella diretta:
- (7)
da cui , .
Definita l'impedenza d'ingresso in una generica posizione x lungo la linea, come il rapporto tra tensione e corrente:
si dimostra che il coefficiente di riflessione può essere espresso come:
- (8)
In particolare, se a fine linea è presente un carico con impedenza , allora a fine linea, ossia a distanza nulla dal carico, l'impedenza d'ingresso coincide con l'impedenza del carico stesso:
pertanto il coefficiente di riflessione a fine linea è pari a:[1]
- (9)
Dalla (9) si evince che:
- se la linea è cortocircuitata alla fine, ossia se , allora e si parla di riflessione negativa, cioè, a fine linea c'è una riflessione totale e l'onda riflessa di tensione, rispetto a quella diretta, è invertita di fase;
- se la linea è aperta alla fine, ossia se , allora e si parla di riflessione positiva, cioè, a fine linea c'è una riflessione totale e l'onda riflessa di tensione, rispetto a quella diretta, non è invertita di fase;
- infine, se , allora , dunque non c'è onda riflessa e si dice che c'è adattamento di impedenza tra il carico e la linea; in tal caso il coefficiente di riflessione è nullo lungo tutta la linea.
Se una linea di trasmissione è non dissipativa (R=0, G=0), come si evince dalla sua espressione la costante di progazione si riduce a un numero immaginario puro:
dunque la costante di attenuazione è nulla:
In tal caso, quindi:
e, poiché l'esponenziale con esponente immaginario è una funzione periodica con modulo unitario, si comprende che con una linea non dissipativa in regime sinusoidale l'onda ti tensione diretta e quella riflessa, dunque anche l'onda di tensione complessiva, hanno ampiezza costante lungo la linea, ossia non subiscono attenuazione, e inoltre il modulo del coefficiente di riflessione è costante lungo la linea. Precisamente, dalla (9) si ha che, qualunque sia la posizione x lungo la linea:
- (10)
Definizione di rapporto di onda stazionaria e proprietà
[modifica | modifica wikitesto]Come abbiamo visto, la tensione in una posizione x lungo la linea è data dalla somma dei contributi dell'onda progressiva e di quella regressiva. In regime sinusoidale:
Se l'onda regressiva è generata da una riflessione che avviene per la presenza di un carico a fine linea, allora si può dire che si tratta della somma tra onda diretta e quella riflessa.
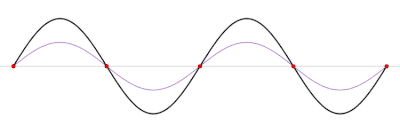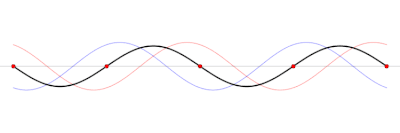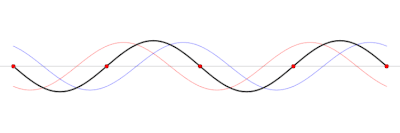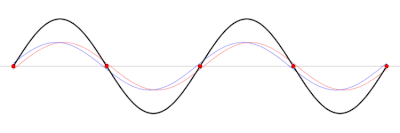
Come è noto, la somma tra un'onda progressiva e un'onda regressiva che abbiano stessa frequenza, stessa velocità di propagazione e stessa ampiezza dà luogo ad un'onda stazionaria. In regime sinusoidale, ad una data frequenza, nel caso di una linea non dissipativa, per la quale non c'è attenuazione e il modulo del coefficiente di riflessione è costante lungo la linea, se tale modulo vale 1, cosa che, come mostra la (9), accade se la linea alla fine è cortocircuitata o aperta, allora onda diretta e onda riflessa hanno la stessa ampiezza e si ottiene soltanto un'onda stazionaria. Se vale 0, non c'è onda riflessa, cosa che accade in caso di adattamento tra carico e linea, e si ha soltanto l'onda progressiva. Negli altri casi, si ha una situazione intermedia tra queste due.
Per descrivere ciò, si definisce ROS (Rapporto di Onda Stazionaria) o anche, in inglese, VSWR (Voltage Standing Wave Ratio), o semplicemente SWR (Standing Wave Ratio), il rapporto tra il valore massimo e il valore minimo del modulo della tensione lungo la linea:
- (11)
Risulta evidente che:[1]
- ci sono particolari punti, lungo la linea, in cui la somma tra onda diretta e onda riflessa dà luogo ad interferenza costruttiva e, per la (7), in tali punti si ha:
dunque tali punti corrispondono a antinodi per l'onda di tensione,
- e particolari punti, lungo la linea, in cui la somma tra onda diretta e onda riflessa dà luogo ad interferenza distruttiva e in tali punti, invece, si ha:
dunque tali punti corrispondono a nodi per l'onda di tensione.
Ma per una linea non dissipativa, come abbiamo visto, il coefficiente di riflessione ha modulo costante espresso dalla (10), dalla quale si deduce anche che:
- (12)
e quindi .
Da ciò segue ancora che possiamo scrivere:
da cui:
- (13)
Dalla (13) risulta evidente che:
- poiché con una linea non dissipativa il modulo del coefficiente di riflessione è costante, allora anche il ROS è costante su tutta la linea;
- inoltre, si ha sempre:
- (14)
e si ha:
- quando , ossia quando il coefficiente di riflessione è nullo, cosa che, come abbiamo visto in precedenza, accade per , ossia quando c'è adattamento di impedenza tra il carico e la linea per cui non c'è onda riflessa;
- quando , cosa che accade se la linea alla fine è cortocircuitata o aperta.
In realtà, poiché con una linea non dissipativa si riduce all'impedenza caratteristica, ossia , la condizione con la quale si ha può essere scritta .
Osserviamo adesso che, come è noto, la potenza assorbita da un carico è proporzionale al quadrato della tensione ad esso applicata. Allora, visto che con una linea non dissipativa il modulo del coefficiente di riflessione è costante, applicando la definizione (7) di coefficiente di riflessione a fine linea dove c'è il carico , si ha:
dove e sono, rispettivamente, la potenza riflessa e la potenza diretta sul carico .
Allora, dalla (13) si ha:
- (15)
Infine, un'altra particolare espressione del ROS può essere ottenuta nel caso in cui una linea non dissipativa termini con un carico puramente resistivo. Infatti, in tal caso, oltre all'impedenza caratteristica , anche l'impedenza del carico diviene un numero reale . Allora, dalla (13) e dalla (10) si ha:
da cui si ottiene:
- (16)
in accordo con la disuguaglianza (14).
Determinare il rapporto di onda stazionaria con la carta di Smith
[modifica | modifica wikitesto]È possibile determinare il di una linea non dissipativa con una semplice procedura anche con la carta di Smith. In particolare, consideriamo la carta di Smith delle impedenze la quale, come è noto, si costruisce tracciando, nel piano complesso in cui le coordinate cartesiane (u,v) sono la parte reale e la parte immaginaria del coefficiente di riflessione, due famiglie di curve, corrispondenti, rispettivamente, ai luoghi dei punti del piano in cui la parte reale e la parte immaginaria dell'impedenza d'ingresso normalizzata hanno un valore costante.
Conoscendo l'impedenza d'ingresso , o il coefficiente di riflessione , in una qualunque posizione lungo una linea non dissipativa, per esempio l'impedenza del carico a fine linea , o il coefficiente di riflessione a fine linea , per determinare il rapporto di onda stazionaria lungo una linea non dissipativa si può procedere nel modo seguente:
- individuare il punto del piano le cui coordinate cartesiane corrispondono al valore del coefficiente di riflessione , che coincide con il punto del piano in cui si intersecano la circonferenza con costante e l'arco di circonferenza con costante corrispondenti al valore dell'impedenza d'ingresso normalizzata
- individuare la circonferenza centrata nell'origine e passante per questo punto del piano; operativamente, la si può tracciare con un compasso
- tale circonferenza interseca l'asse delle ascisse (asse delle u) in due punti disposti simmetricamente rispetto all'origine: con ascissa u negativa e con ascissa u positiva
- allora il è uguale al valore di corrispondente alla circonferenza con costante passante per , mentre il valore di relativo a è pari a .
Tuttavia, in molte carte di Smith moderne è presente una scala in basso graduata in modo tale che, per leggere il valore del , occorre tracciare con un righello una linea verticale verso il basso dal punto invece che dal punto .
Osserviamo, infine, che, data una linea di trasmissione non dissipativa, per il fatto che, nel piano complesso della carta di Smith, lungo le circonferenze centrate nell'origine il modulo del coefficiente di riflessione è costante, e quindi, per la (13), è costante anche il rapporto di onda stazionaria, tali circonferenze sono dette circonferenze a costante.[2][3]
Implicazioni pratiche del rapporto di onda stazionaria
[modifica | modifica wikitesto]La situazione più comune in cui occorre misurare e tenere conto del ROS si presenta durante l'installazione e l'accordo di antenne trasmittenti. Quando un trasmettitore è connesso ad un'antenna mediante una linea di trasmissione, l'l'impedenza nel punto di alimentazione dell'antenna deve essere adattata all'impedenza caratteristica della linea affinché l'impedenza vista dal trasmettitore sia quella per cui è stato progettato (che di norma coincide con l'impedenza caratteristica della linea, solitamente 50 o 75 ohm).
L'impedenza di un'antenna può variare a causa di una gran quantità di fattori che non sempre possono essere identificati chiaramente. Questi includono la frequenza del trasmettitore (da confrontare con la frequenza di risonanza per cui l'antenna è stata progettata), l'altezza dell'antenna rispetto al suolo e la qualità di quest'ultimo come piano di terra, vicinanza a grosse strutture metalliche e variazioni nella dimensione esatta dei conduttori utilizzati per costruire l'antenna.[4]
Quando un'antenna e una linea non hanno impedenze adattate, l'impedenza vista dal trasmettitore è diversa da quella per cui è stato progettato, dunque il trasmettitore potrebbe non essere in grado di trasferire tutta la sua potenza all'antenna e, in alcuni casi, ciò può persino danneggiare il trasmettitore stesso.[5] La potenza riflessa nella linea di trasmissione aumenta le correnti e perciò le perdite nella linea rispetto alla potenza effettivamente trasferita al carico.[6] È l'interazione di queste onde riflesse con le onde dirette a produrre le onde stazionarie,[5] con le ripercussioni negative che abbiamo elencato.[7]
L'adattamento dell'impedenza dell'antenna all'impedenza della linea a volte può essere ottenuto regolando l'antenna stessa, altrimenti si può utilizzare un accordatore d'antenna, particolare dispositivo per l'adattamento di impedenza. L'installazione di un accordatore tra la linea e l'antenna consente alla linea di vedere un valore di impedenza di carico vicina alla sua impedenza caratteristica, mentre trasferisce la maggior parte della potenza del trasmettitore (una piccola parte può essere dissipata all'interno dell'accordatore) affinché venga irradiata dall'antenna, nonostante il valore non adattato dell'impedenza nel punto di alimentazione. Anche l'installazione di un accordatore tra il trasmettitore e la linea di trasmissione può trasformare l'impedenza vista all'estremità della linea con il trasmettitore ad una adatta allo stesso trasmettitore. Tuttavia, in quest'ultimo caso, nella linea di trasmissione è ancora presente un ROS elevato, con il conseguente aumento delle perdite nella linea che non vengono limitate.
L'ordine di grandezza di queste perdite dipende dal tipo di linea di trasmissione e dalla sua lunghezza. Queste perdite aumentano sempre con la frequenza. Per esempio, potrebbe accadere che una certa antenna usata ben lontano dalla sua frequenza di risonanza abbia un ROS di 6:1. Per una frequenza di 3,5 MHz, con tale antenna alimentata mediante 75 metri di cavo coassiale RG-8A, la perdita dovuta alle onde stazionarie sarebbe di 2,2 dB. Tuttavia, lo stesso disadattamento di 6:1 attraverso 75 metri di cavo coassiale RG-8A determinerebbe una perdita di 10,8 dB a 146 MHz.[5] Dunque, un adattamento migliore dell'antenna alla linea di trasmissione, cioè avere un ROS più basso, diviene sempre più importante all'aumentare della frequenza, anche se il trasmettitore è in grado di adattare l'impedenza (o viene utilizzato un accordatore d'antenna tra il trasmettitore e la linea di trasmissione).
Alcuni tipi di trasmissioni possono soffrire di altri effetti negativi dovuti a onde riflesse su una linea di trasmissione. La TV analogica può sperimentare "segnali fantasma" dovuti a segnali ritardati che rimbalzano avanti e indietro su una linea lunga. Anche l'FM stereo può subire effetti negativi e i segnali digitali possono presentare impulsi ritardati che portano a errori di bit. Si verificano effetti ogni volta che i tempi di ritardo per un segnale che torna indietro e poi di nuovo su per la linea, verso l'antenna, sono comparabili con le costanti di tempo della modulazione. Per questa ragione, questi tipi di trasmissione richiedono un basso ROS sulla linea di trasmissione, anche se la perdita indotta dal ROS potrebbe essere accettabile e l'adattamento viene effettuato sul trasmettitore.
Metodi di misura
[modifica | modifica wikitesto]
Si possono usare numerosi metodi per misurare il rapporto di onda stazionaria. Il metodo più intuitivo fa uso di una linea di trasmissione tagliata sulla parte esterna in modo da realizzare una piccola scanalatura così da ottenere un alloggiamento che permetta di inserire una sonda per misurare la tensione istantanea in vari punti lungo la linea.[8] In tal modo il valore massimo e quello minimo possono essere comparati direttamente. Questo metodo è usato in VHF e a frequenze più elevate. A frequenze più basse, questo metodo può diventare impraticabile per la lunghezza delle linee. Si possono usare accoppiatori direzionali dalle HF fino a frequenze nel campo delle microonde. Alcuni sono lunghi un quarto di lunghezza d'onda o più, il che restringe il loro uso alle frequenze più elevate. Altri tipi di accoppiatore direzionale campionano la corrente e la tensione in un singolo punto della linea di trasmissione e matematicamente combinano questi valori in modo tale da rappresentare la potenza che fluisce in una direzione.[9]. Il tipo comune di rosmetro/wattmetro usato in ambito radioamatoriale può contenere un accoppiatore direzionale duale. Altri tipi utilizzano un singolo accoppiatore che può essere ruotato di 180 gradi per campionare il flusso di potenza in entrambe le direzioni. Accoppiatori non direzionali di questo tipo sono disponibili per molti intervalli di frequenza e livelli di potenza e con valori di accoppiamento appropriati per il misuratore analogico utilizzato.

La potenza diretta e la potenza riflessa misurate dagli accoppiatori direzionali possono essere utilizzate per calcolare il ROS. Questi calcoli possono essere fatti matematicamente in forma analogica o digitale o utilizzando metodi grafici integrati nello strumento di misura sotto forma di scala aggiuntiva o leggendo il valore dal punto in cui si incrociano due aghi sullo stesso strumento.
Gli strumenti di misura descritti sopra possono essere usati "in linea" cioè tutta la potenza del trasmettitore può passare attraverso lo strumento e ciò consente un monitoraggio continuo del ROS. Altri strumenti, quali analizzatori di reti, accoppiatori direzionali a bassa potenza e circuiti a ponte realizzati con antenne, usano bassa potenza per la misurazione e possono essere connessi al posto del trasmettitore. I circuiti a ponte possono essere usati per misurare direttamente la parte reale e la parte immaginaria dell'impedenza del carico e per ricavare il ROS da questi valori. Questi metodi possono fornire maggiori informazioni rispetto al solo ROS o alla sola potenza diretta e riflessa.[10] Gli analizzatori di antenna stand alone utilizzano vari metodi di misurazione e possono visualizzare il ROS e altri parametri graficati al variare della frequenza. Usando in combinazione degli accoppiatori direzionali e un circuito a ponte, è possibile realizzare uno strumento in linea che legge direttamente l'impedenza complessa o il ROS.[11] Sono disponibili anche analizzatori d'antenna stand alone che misurano parametri multipli.
Note
[modifica | modifica wikitesto]- ^ a b c Marcello Carlà, Appunti di Elettronica per Fisici, Cap. 2: Linee di trasmissione (PDF), Università degli Studi di Firenze - Dipartimento di Fisica, A.A. 2019-2020. URL consultato il 4 febbraio 2022 (archiviato dall'url originale il 4 febbraio 2022).
- ^ Smith Chart Tutorial (PDF), su ieee.li. URL consultato il 3 febbraio 2022.
- ^ Smith Chart Calculations (PDF), su arrl.org. URL consultato il 3 febbraio 2022.
- ^ Chuck, ed. Hutchinson, The ARRL Handbook for Radio Amateurs 2001, Newington, CT, ARRL—the national association for Amateur Radio, 2000, p. 20.2, ISBN 978-0-87259-186-8.
- ^ a b c Chuck, ed. Hutchinson, The ARRL Handbook for Radio Amateurs 2001, Newington, CT, ARRL—The national association for Amateur Radio, 2000, pp. 19.4–19.6, ISBN 978-0-87259-186-8.
- ^ Steve Ford, The SWR Obsession (PDF), in QST, vol. 78, n. 4, Newington, CT, ARRL—The national association for Amateur Radio, April 1997, pp. 70–72. URL consultato il 4 novembre 2014.
- ^ Chuck, ed. Hutchinson, The ARRL Handbook for Radio Amateurs 2001, Newington, CT, ARRL—the national association for Amateur Radio, 2000, p. 19.13, ISBN 978-0-87259-186-8.
- ^ Fredrick E. Terman, Electronic Measurements, McGraw Hill, 1952 Library of Congress Catalog Number: 51-12650 p.135ff
- ^ How Does an SWR Meter Really Work, in Glenn B. Schulz W9IQ, 24 gennaio 2018. URL consultato il 18 marzo 2018.
- ^ Nautel Adds Two Models to NX Series, in Nautel, 11 marzo 2015. URL consultato il 6 luglio 2017 (archiviato dall'url originale il 18 agosto 2016).
- ^ Delta Electronics, Inc. Model OIB-1 and OIB-3, su deltaelectronics.com.
Voci correlate
[modifica | modifica wikitesto]- Rosmetro
- Linea di trasmissione
- Carta di Smith
- Adattamento di impedenza
- Accordatore d'antenna
- Parametri s
- Return loss
- Impedenza caratteristica
| Controllo di autorità | GND (DE) 4502840-0 |
|---|




![{\displaystyle \ \ \ V(x,t)=Re[\mathbf {V} (x,t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4f1906b49c47e1e24b9f4b1552e7f2172d44fa16)

![{\displaystyle \ \ \ \ I(x,t)=Re[\mathbf {I} (x,t)]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8ea30933e4046f6a78c7c46f9e8a605cf47562cc)





![{\displaystyle {\begin{aligned}\gamma ={\sqrt {\mathbf {Z} \mathbf {Y} }}={\sqrt {(R+j\omega L)(G+j\omega C)}}\\[6pt]={\sqrt {LC}}{\sqrt {-\omega ^{2}+j\omega \left({\frac {R}{L}}+{\frac {G}{C}}\right)+{\frac {RG}{LC}}}}\\[6pt]\end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/63dee9b5c6f289c2dc5795f94e471abdef5faf34)



![{\displaystyle \ \mathbf {I} (x)={\frac {1}{\mathbf {Z_{0}} }}[\mathbf {V_{1}} e^{-\gamma x}-\mathbf {V_{2}} e^{\gamma x}]={\frac {1}{\mathbf {Z_{0}} }}[\mathbf {V_{1}} e^{-\alpha x}e^{-j\beta x}-\mathbf {V_{2}} e^{\alpha x}e^{j\beta x}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a93cf41dd1c3cbd4a450c7a4642dab95c453f830)









![{\displaystyle \ \rho (x)=[\rho (x=0)]e^{2\gamma x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1a1654d8e68aa1b7ce5b4c8d94abd57051eaa795)

















![{\displaystyle \ \rho (x)=[\rho (x=0)]e^{2j\beta x}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/51405b32292bb2b08e5707b888e895c8c34411b5)







































