Utente:Prof. L. Smaltese/Sandbox

Aiuto:Pagina delle prove Aiuto:Guida essenziale Aiuto:Tour guidato Aiuto:FAQ Aiuto:Dove fare una domanda Ti diamo il benvenuto nella pagina delle prove (o sandbox) di Wikipedia! Lo scopo della presente pagina è quello di permettere liberamente di fare degli esperimenti senza conseguenze su pagine attive. Per fare le prove clicca sulla linguetta Modifica wikitesto, scrivi, usa il pulsante Visualizza anteprima e, quando sei soddisfatto, clicca sul tasto Pubblica le modifiche. Il tuo testo non rimarrà a lungo: la pagina è sovente sovrascritta da altri utenti e ripulita regolarmente. Per maggiori informazioni, vedi Aiuto:Pagina delle prove. Se vuoi fare una prova di modifica con la nuova interfaccia di modifica VisualEditor puoi utilizzare la relativa pagina delle prove o la funzionalità dedicata. Se sei un utente registrato, puoi anche decidere di usare una sandbox personale. Benché sia una pagina delle prove, anche questa pagina deve sottostare alle linee guida di Wikipedia in materia di comportamenti degli utenti e diritto d′autore. Quindi non devi mai inserirvi contenuti sotto copyright od offensivi o financo diffamatori. A titolo d′esempio, non è permesso fare copia-incolla da altri siti Internet (nemmeno fosse il tuo sito web personale!), perché, salvo poche eccezioni, è una violazione della legge.

Buon lavoro. In geometria euclidea, il teorema diretto dei triangoli isosceli, noto anche come pons asinorum, afferma che gli angoli opposti i due lati uguali di un triangolo isoscele sono congruenti. Si tratta, in sostanza, il contenuto della proposizione 5 nel libro I degli Elementi di Euclide.

Pons asinorum

In epoca medievale, quando la geometria rappresentava uno dei quattro soggetti del Quadrivium, questo teorema assunse la reputazione di una difficile prova per un principiante, chi non avesse la padronanza della sua dimostrazione non sarebbe stato in grado di procedere con degli studi più avanzati. Forse per questo il teorema divenne noto come il pons asinorum o ponte degli asini. Questo termine è usato come metafora per una prova che permetta una selezione tra chi è più dotato in una materia e chi meno.

Dimostrazioni

Euclide and Proclo

Gli Elementi di Euclide Libro 1 proposizione 5; pons asinorum

L'enunciato del teorema di Euclide include una seconda conclusione, che se i lati uguali del triangolo sono prolungati sotto la base, allora gli angoli tra le estensioni e la base sono uguali. La dimostrazione di Euclide consiste nel definire le linee ausiliarie per queste estensioni. Ma, nel commentare Euclide, Proclo mette in evidenza che Euclide non usa mai la seconda conclusione e la sua dimostrazione può essere semplificato in qualche modo tracciando le linee ausiliarie ai lati del triangolo, mentre il resto della dimostrazione si esegue più o meno allo stesso modo. Ci sono state molte speculazioni e dibattiti sul perché Euclide abbia aggiunto la seconda conclusione al teorema teorema, dal momento che rende la dimostrazione più complicata. Una spiegazione plausibile, data da Proclo, è che la seconda conclusione possa essere utilizzata in eventuali obiezioni alle dimostrazioni successive di proposizioni in cui Euclide non copre tutti i casi. La Dimostrazione si basa su quello che è oggi chiamato Lato-Angolo-Lato, ovvero la proposizione precedente negli Elementi.

La dimostrazione di Proclo

La variante di Proclo alla dimostrazione di Euclide procede come segue: sia ABC un triangolo isoscele con AB e AC i lati uguali. Si scelga un punto arbitrario D sul lato AB e si prenda il punto E su CA in modo che $AD\cong AE\,$. Tracciate le linee di BE, DC e DE si consideri i triangoli BAE e CAD, questi triangoli hanno $BA\cong AC\,$, $AE\cong AD\,$, e l'angolo ${\hat {A}}$ coincidente, quindi per il criterio di congruenza lato-angolo-lato i triangoli BAE e CAD sono congruenti e pertanto i lati e gli angoli corrispondenti saranno congruenti: l'angolo $A{\hat {B}}E$ è uguale all'angolo $A{\hat {C}}D$, l'angolo $A{\hat {D}}C$ è uguale all'angolo $A{\hat {E}}B$, e $BE\cong CD\,$. Dal momento che $AC\cong AB\,$ e $AD\cong AE\,$, $BD\cong CE\,$ per sottrazione di parti uguali. Si consideri ora i triangoli DBE e ECD; per essi $BD\cong CE\,$, $BE\cong CD\,$, e l'angolo $D{\hat {B}}E$ è uguale all'angolo $E{\hat {C}}D$ come è stato appena mostrato, quindi ancora per il criterio lato-angolo-lato, i triangoli sono congruenti: l'angolo $B{\hat {D}}E$ è uguale all'angolo $C{\hat {E}}D$. (La congruenza implica anche $DF\cong FD\,$, ma questo è evidente). Poiché l'angolo $B{\hat {D}}E$ è uguale all'angolo $C{\hat {E}}D$ e l'angolo $C{\hat {D}}E$ è uguale all'angolo $B{\hat {E}}D$, allora l'angolo $B{\hat {D}}C$ sarà uguale all'angolo $C{\hat {E}}B$ per sottrazione di parti uguali. Consideriamo una terza coppia di triangoli, BDC e CEB; $DB\cong CE\,$, $DC\cong EB\,$, e l'angolo $B{\hat {D}}C$ uguale all'angolo $C{\hat {E}}B$, quindi applicando lato-angolo-lato una terza volta, si dimostra che i due triangoli sono congruenti. In particolare, l'angolo $C{\hat {B}}D\cong B{\hat {C}}E$, come volevasi dimostrare.

Pappo

Proclo presenta una dimostrazione molto più corta attribuita a Pappo di Alessandria. Essa non è solo più semplice, ma non richiede costruzioni aggiuntive. Il metodo di dimostrazione applicato è il criterio lato-angolo-lato tra un triangolo e la sua immagine speculare. Altri autori moderni, descrivono questo metodo di dimostrazionecome prendere il triangolo, capovolgerlo e posarlo su se stesso. Questo metodo è oggetto di satira da parte di Charles Dodgson in Euclide ed i suoi rivali moderni, che lo definisce un "Irish bull", ovverosia un non senso, poiché apparentemente richiede che il triangolo si trovi in due posti contemporaneamente.

La dimostrazione è la seguente: Sia ABC un triangolo isoscele con $AB$ e $AC$ i suoi due lati congruenti. Si considerino i triangoli ABE e ACB, dove ACB è un secondo triangolo con vertici ${\hat {A}}$, ${\hat {C}}$ e ${\hat {B}}$ corrispondenti rispettivamente ai vertici ${\hat {A}}$, ${\hat {B}}$ e ${\hat {C}}$ nel triangolo originale. Si avrà $AB\cong AC$, $AC\cong AB$ e l'angolo ${\hat {A}}$ uguale a se se stesso, così per il criterio lato-angolo-lato, i triangoli ABC e ACB sono congruenti. In particolare l'angolo ${\hat {B}}$ è congruente all'angolo ${\hat {C}}$.

Altro

Dimostrazione dei libri di testo

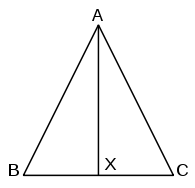
La dimostrazione standard dei libri di testo consiste nel costruire la bisettrice dell'angolo ${\hat {A}}$ . Questa è più semplice della dimostrazione di Euclide, ma euclide non presenta la costruzione della bisettrice di un angolo prima della proposizione 9. Così l'ordine della presentazione delle proposizioni di Euclide deve essere cambiato per evitare un ragionamento circolare.

La dimostrazione procede come segue: come prima consideriamo il triangolo ABC con $AB\cong AC$. Costruiamo la bisettrice dell'angolo ${\widehat {BAC}}\,$ e prolungarla fino a incontrare il lato $BC$ nel punto X. Nei triangoli BAX e CAX si ha $AB\cong AC\,$, $AX$ coincidente. Inoltre l'angolo $B{\hat {A}}X\cong C{\hat {A}}X$, così, per il criteriolato-angolo-lato, BAX e CAX sono congruenti. Segue che gli angoli ${\hat {B}}$ e ${\hat {C}}$ sono congruenti.

Legendre usa una costruzione simile in Éléments de géométrie, ma considerando il punto X come punto medio del segmento BD. La dimostrazione è simile ma usa il criterio Lato-Lato-Lato al posto di lato-angolo-lato, ma lato-lato-lato non è è mostrato che molto più avanti da Euclide negli Elementi.

Prodotto interno

Il teorema diretto dei triangoli isosceli equivale al prodotto interno su numeri reali o complessi. In questi spazi equivale a prendere dei vettori x, y e z tali che

$x+y+z=0{\text{ and }}\|x\|=\|y\|,\,$

quindi

$\|x-z\|=\|y-z\|.\,$

Mentre

$\|x-z\|^{2}=\|x\|^{2}-2x\cdot z+\|z\|^{2},\,$

e

$x\cdot z=\|x\|\|z\|\cos \theta \,$

dove θ è l'angolo tra i due vettori, la conclusione di questa forma del teorema equivale ad enunciare l'uguaglianza degli angoli.

Note e riferimenti

• Euclid, commentary and trans. by T. L. Heath Elements Vol. 1 (1908 Cambridge) Google Books

• Euclid, commentary by Proclus, ed. and trans. by T. Taylor Elements Vol. 2 (1789) Google Books

• Geometry Textbook - Standard IX, Maharashtra State Board of Secondary and Higher Secondary Education, Pune - 411 005, India.
• John Stillwell, The Four Pillars of Geometry, Springer, 2005, page 24.

Voci correlate

• Triangolo isoscele

[[Categoria:Geometria del triangolo]]