Problema dei topi

In matematica, nel problema dei topi - anche chiamato problema degli scarabei - $n$ topi partono dai vertici di un poligono regolare di $n$ lati di lunghezza unitaria, ed ogni topo si dirige verso il compagno più vicino, muovendosi in senso antiorario ed a velocità costante. Il problema chiede di determinare la traiettoria di ciascun topo, ed il loro punto di incontro.

Soluzione[modifica | modifica wikitesto]

Ogni topo traccia una spirale logaritmica (che nel caso $n=2$ degenera in una retta), tutti gli animali si incontrano nel centro del poligono e percorrono una distanza - dipendente dal numero $n$ di lati del poligono - pari a

d_{n}={\frac {1}{1-\cos \left({\frac {2\pi }{n}}\right)}}

n = 2[modifica | modifica wikitesto]

In questo caso i due topi percorrono uno spazio, ricavabile dalla formula

d_{2}={\frac {1}{1-\cos \left({\frac {2\pi }{2}}\right)}}={\frac {1}{2}}

e quindi si incontrano nel centro del segmento. Si noti che, dato che la velocità dei due topi è la medesima ed essi si muovono su una linea retta, questo risultato era ampiamente prevedibile.

n = 3[modifica | modifica wikitesto]

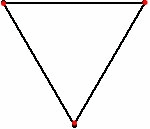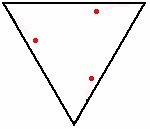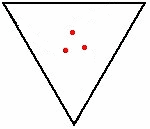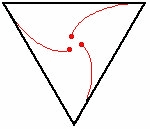
Nel caso del triangolo è ben visibile la traiettoria a spirale logaritmica. Lo spazio percorso è sempre ricavabile come

d_{3}={\frac {1}{1-\cos \left({\frac {2\pi }{3}}\right)}}={\frac {2}{3}}

n = 6[modifica | modifica wikitesto]

All'aumentare del numero dei lati del poligono aumenta la distanza percorsa dai topi, che comunque si incontrano nel centro della figura. Nel caso dell'esagono abbiamo che

d_{6}={\frac {1}{1-\cos \left({\frac {2\pi }{6}}\right)}}=2

Generalizzazioni[modifica | modifica wikitesto]

Il problema può essere generalizzato anche nel caso di poligoni non regolari, nel caso di topi che si muovono a diverse velocità e con punti di partenza diversi. Il problema dei topi in sé potrebbe sembrare una semplice curiosità matematica, invece può essere esteso ad altri campi, come ad esempio quello militare dell'analisi delle traiettorie dei missili a ricerca termica.