Contrazione degli spigoli
Nella teoria dei grafi, una contrazione dei grafi è un'operazione che rimuove uno spigolo da un grafo mentre fonde simultaneamente i due vertici che connetteva in precedenza. La contrazione degli spigoli è un'operazione fondamentale nella teoria dei minori dei grafi. L'identificazione dei vertici è una forma meno restrittiva di questa operazione.
Definizione[modifica | modifica wikitesto]
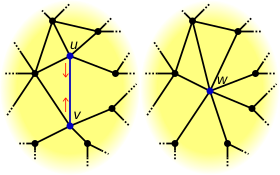
L'operazione di contrazione degli spigoli si manifesta in relazione a un particolare spigolo, e. Lo spigolo e è rimosso e i suoi due vertici incidenti, u e v, sono fusi in un nuovo vertice w, dove gli spigoli incidenti su w corrispondono ciascuno a uno spigolo incidente su u o su v.
Più generalmente, l'operazione può essere eseguita su un insieme di spigoli contraendo ciascuno spigolo (in qualsiasi ordine). Le contrazioni possono dare come risultato un grafo con cappi o spigoli multipli. Questi sono talvolta cancellati per mantenerli dentro la classe dei grafi semplici.
Definizione formale[modifica | modifica wikitesto]
Sia G=(V,E) un grafo (o grafo diretto) contenente uno spigolo e=(u,v) with u≠v. Sia f una funzione che mappa ogni vertice in V\{u,v} su sé stesso ovvero lo mappa su un nuovo vertice w. La contrazione di e dà come risultato un nuovo grafo G′=(V′,E′), dove V′=(V\{u,v})∪{w}, E′=E\{e}, e per ogni x∈V, x′=f(x)∈V′ è incidente su uno spigolo e′∈E′ se e solo se, lo spigolo corrispondente, e∈E, è incidente su x in G.
Identificazione dei vertici[modifica | modifica wikitesto]
L'identificazione dei vertici (talvolta chiamata contrazione dei vertici) rimuove la restrizione che la contrazione debba avvenire sui vertici che condividono uno spigolo incidente. (Quindi, la contrazione degli spigoli è un caso speciale dell'identificazione dei vertici.) L'operazione può avvenire su qualsiasi coppia (o sottoinsieme) di vertici nel grafo. I vertici tra due vertici in contrazione sono talvolta rimossi. Se v e v' sono vertici di componenti distinti di G, allora possiamo creare un nuovo grafo G' identificando v e v' in G come un nuovo vertice v in G'.[1]
Separazione dei vertici[modifica | modifica wikitesto]
La separazione dei vertici, che è la stessa cosa della divisione dei vertici, significa che un vertice separato in due, dove questi due nuovi vertici sono adiacenti ai vertici ai quali era a sua volta adiacente il vertice originario. Questa è l'operazione inversa dell'identificazione dei vertici.
Contrazione dei cammini[modifica | modifica wikitesto]
La contrazione dei cammini avviene sull'insieme degli spigoli in un cammino che si contraggono per formare un unico spigolo tra gli estremi del cammino. Gli spigoli incidenti sui vertici lungo il cammino sono o eliminati, o arbitrariamente (o sistematicamente) connessi a uno degli estremi.
Torsione[modifica | modifica wikitesto]
Dati due grafi disgiunti G1 e G2, dove G1 contiene i vertici u1 e v1 e G2 contiene i vertici u2 e v2. Si supponga che possiamo ottenere il grafo G identificando i vertici u1 di G1 e u2 di G2 come il vertice u di G e identificando i vertici v1 di G1 e v2 di G2 come il vertice v di G. In una torsione (twisting) G' di G rispetto all'insieme dei vertici {u, v}, noi identifichiamo, invece, u1 con v2 e v1 con u2.[2]
Applicazioni[modifica | modifica wikitesto]
Sia la tecnica di contrazione degli spigoli sia quella dei vertici sono preziose nella prova per induzione sul numero dei vertici o degli spigoli in un grafo, dove si può assumere che una proprietà vale per tutti i grafi più piccoli e questo può essere usato per dimostrare la proprietà per il grafo più grande.
Le contrazioni sono utili anche in strutture dove desideriamo semplificare un grafo identificando i vertici che rappresentano entità essenzialmente equivalenti. Uno dei più comuni esempi è la riduzione di un grafo diretto generale a un grafo aciclico diretto contraendo tutti i vertici in ciascuna componente fortemente connessa. Se la relazione descritta dal grafo è transitiva, nessuna informazione si perde finché etichettiamo ogni vertice con l'insieme di etichette dei vertici che sono stati contratti per formarlo.
Un altro esempio è la riunione eseguita nell'allocazione dei registri della colorazione globale dei grafi, in cui i vertici sono contratti (dove è sicuro) per eliminare operazioni di spostamento tra distinte variabili.
La contrazione degli spigoli si usa nei pacchetti di modellazione tridimensionale (o manualmente, o attraverso qualche caratteristica del software di modellazione) per ridurre coerentemente il conteggio dei vertici, aiutando nella creazione dei modelli con basso numero di poligoni.
Note[modifica | modifica wikitesto]
Voci correlate[modifica | modifica wikitesto]
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) Eric W. Weisstein, Contrazione degli spigoli, su MathWorld, Wolfram Research.