Digrafo aciclico
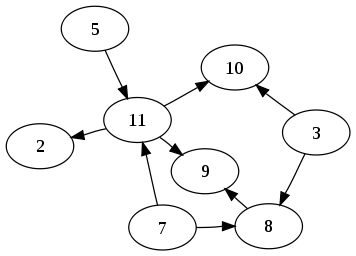
In matematica e informatica un grafo aciclico diretto oppure grafo aciclico orientato (in inglese Directed acyclic graph, DAG) è un particolare tipo di digrafo (anche noto come "grafo diretto") che non ha cicli (circuiti) diretti, ovvero comunque scegliamo un vertice del grafo non possiamo tornare ad esso percorrendo gli archi del grafo. Un grafo diretto può dirsi aciclico (cioè è un DAG) se una visita in profondità non presenta archi all'indietro.[1][2][3]
I DAG sono usati per rappresentare diversi tipi di strutture sia in matematica che in informatica. Per esempio una serie di lavori che devono essere ordinati in modo tale che alcuni di essi debbano essere eseguiti prima di altri (per esempio le applicazioni da eseguire durante l'avvio di un computer) possono essere rappresentati con un DAG dove ogni vertice rappresenta un lavoro e ogni arco la relazione di dipendenza, cioè se c'è un arco che va da A a B vuol dire che A deve essere eseguito prima di B; l'algoritmo per l'ordinamento topologico rappresenta una buona soluzione al problema. I DAG possono anche essere usati per rappresentare in modo efficiente una serie di sequenze che si sovrappongono.
Fra i grafi non diretti (cioè i grafi nei quali ogni arco può essere percorso in tutte e due le direzioni) il corrispondente del DAG o grafo aciclico è l'albero.
Pozzi e sorgenti[modifica | modifica wikitesto]
In un DAG si definiscono "pozzi" tutti i nodi che rappresentano la fine di almeno un arco ma non rappresentano l'inizio di nessun arco. Si definiscono "sorgenti" tutti i nodi che sono inizio di almeno un arco ma non rappresentano la fine di nessun arco.
Ordinamento topologico[modifica | modifica wikitesto]
Su qualsiasi DAG è possibile creare un ordinamento topologico, cioè si dispongono in ordine tutti i nodi in modo tale che non ci sia nessun arco all'indietro, in altri termini se esiste un arco che va da A a B allora necessariamente A comparirà nell'ordinamento prima di B. L'ordinamento topologico di un DAG esiste sempre, ma non è necessariamente unico.
Un algoritmo per creare un ordinamento topologico può essere quello di inserire alla fine dell'ordinamento tutti i pozzi, poi "strappare" i pozzi dal DAG e ripetere l'ordinamento finché il DAG non è vuoto. Un algoritmo efficiente (in O(N+M) dove N è il numero di nodi e M il numero di archi) consiste nell'effettuare una visita in profondità del grafo inserendo nell'ordinamento un nodo solo quando sono stati visitati tutti i suoi vicini.
Note[modifica | modifica wikitesto]
- ^ Nicos Christofides, Graph theory: an algorithmic approach, Academic Press, 1975, pp. 170–174..
- ^ K. Thulasiraman e M. N. S. Swamy, 5.7 Acyclic Directed Graphs, in Graphs: Theory and Algorithms, John Wiley and Son, 1992, p. 118, ISBN 978-0-471-51356-8..
- ^ Jørgen Bang-Jensen, 2.1 Acyclic Digraphs, in Digraphs: Theory, Algorithms and Applications, Springer Monographs in Mathematics, 2nd, Springer-Verlag, 2008, pp. 32–34, ISBN 978-1-84800-997-4..
Voci correlate[modifica | modifica wikitesto]
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file sul digrafo aciclico
Wikimedia Commons contiene immagini o altri file sul digrafo aciclico
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) Eric W. Weisstein, Digrafo aciclico, su MathWorld, Wolfram Research.
| Controllo di autorità | GND (DE) 4143834-6 |
|---|