Codice Gray
Il codice Gray è un codice binario a lunghezza fissa, con la caratteristica che due qualsiasi sue posizioni consecutive hanno solo un carattere diverso tra loro. Fu progettato e brevettato[1] nel 1953 dal ricercatore Frank Gray dei laboratori Bell.
Si possono usare codici di Gray di tutte le lunghezze: il codice di lunghezza s è costituito da tutte le sequenze di s bit e consente di rappresentare tutti gli interi da 0 a .
Esso differisce dalla notazione posizionale binaria degli interi in quanto prevede che si passi da un intero al successivo modificando un solo bit; questa caratteristica (detta a cambio 1) semplifica e rende meno soggette ad errori le operazioni di dispositivi elettronici che devono scorrere informazioni organizzate in sequenze. Evidentemente la codifica di Gray risulta poco sensata per interi da sottoporre ad operazioni come somme o prodotti.

Diversi dispositivi elettronici di acquisizione di posizione, tra cui gli encoder (lineari o rotativi, come - per esempio - i regolatori di volume digitali negli impianti Hi-Fi), codificano il valore digitale della posizione chiudendo o aprendo una serie di contatti elettrici o barriere ottiche. Questi dispositivi devono produrre, in base alla misura della posizione rilevata, un particolare numero in base 2. Ad esempio, ruotando la manopola di un encoder a 3 bit, si potrebbe ottenere in output il valore '001'. Grazie alla corretta interpretazione di questo numero, si può conoscere la misura della posizione del dispositivo.
Motivazione[modifica | modifica wikitesto]
Molti dispositivi elettronici indicano la propria posizione chiudendo e aprendo degli interruttori. Se queste posizioni venissero rappresentate come quelle di una codifica binaria ordinata in modo naturale, le posizioni 3 e 4 sarebbero consecutive, ma avrebbero tutti i bit di valore diverso:
| Decimale | Binario |
|---|---|
| ... | ... |
| 3 | 011 |
| 4 | 100 |
| ... | ... |
Questa situazione è difficile da rappresentare con degli interruttori fisici reali: è molto improbabile che tutti gli interruttori cambino il proprio stato (aperto/chiuso) esattamente nello stesso istante. Durante il passaggio tra i due stati mostrati nella precedente tabella, tutti e tre gli interruttori dovranno cambiare stato, probabilmente producendo dei valori che oscillano per il breve periodo del cambiamento.
Anche se idealmente, si fosse in assenza di queste oscillazioni degli interruttori, il cambiamento di stato potrebbe comunque apparire come una sequenza di stati intermedi tra 001 e 100:
011, 001, 101, 100
Questa inusuale sequenza è dovuta al fatto che la commutazione degli interruttori non avviene contemporaneamente, ma solo un interruttore alla volta. In casi come questi, un osservatore esterno non può sapere se la posizione 001 (o qualsiasi altra posizione misurata) è una "vera" posizione, oppure uno stato intermedio tra due posizioni, quindi il sistema potrebbe memorizzare un valore intermedio "falso".
Questo problema, relativo all'ambiguità della posizione, è causato dal fatto di aver utilizzato una numerazione binaria ordinata in modo naturale, e può essere risolta usando un altro tipo di numerazione, che utilizza una codifica in cui si commuta un solo interruttore alla volta (un solo bit alla volta).
Va notato che anche nel passaggio dall'ultima alla prima parola del codice cambia solamente un bit.
Il codice Gray è un codice "riflesso".
Costruzione[modifica | modifica wikitesto]
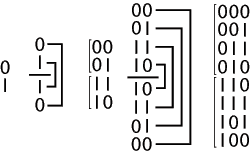
Un codice Gray ad n-bit si costruisce attraverso un algoritmo ricorsivo. Si parte dal primo bit, quello meno significativo, si mette uno 0 sopra ed un 1 sotto.
Al passo successivo, si mette una riga al di sotto dell'1, come se fosse uno specchio, e si ricopiano le cifre invertendo l'ordine, con la riga che funge da specchio, appunto. Si termina inserendo uno 0 davanti alla sequenza costruita se questa è sopra la riga, altrimenti si aggiunge un 1. Ora siamo arrivati ad un codice con 2 bit.
Iterando i passi precedenti, si mette la riga, si specchia la sequenza e si aggiunge il bit più significativo, si costruiscono codici ad n-bit.
Esempi[modifica | modifica wikitesto]
Codice Gray a 2 bit 00 01 11 10
Codice Gray a 3 bit 000 001 011 010 110 111 101 100
Codice Gray a 4 bit 0000 0001 0011 0010 0110 0111 0101 0100 1100 1101 1111 1110 1010 1011 1001 1000
Codice Gray a 5 bit 00000 00001 00011 00010 00110 00111 00101 00100 01100 01101 01111 01110 01010 01011 01001 01000 11000 11001 11011 11010 11110 11111 11101 11100 10100 10101 10111 10110 10010 10011 10001 10000
Conversione[modifica | modifica wikitesto]
Da binario a Gray[modifica | modifica wikitesto]
Per convertire un numero in base due in codice di Gray viene eseguito un semplice procedimento:
Il primo bit (MSB) in codifica binaria rimane uguale e viene, quindi, riportato; si esegue poi lo XOR tra il numero in codifica binaria e lo stesso numero spostato di una cifra verso destra, come nel seguente esempio:
bin: 110010 XOR
110010
Gray: 101011
La prima cifra del codice Gray (Most Significant Bit) è la stessa della codifica binaria, le altre sono il risultato dello XOR tra ogni cifra in codifica binaria e la cifra successiva.
Da Gray a binario[modifica | modifica wikitesto]
Il procedimento di conversione da codice di Gray a codifica binaria normale è molto simile a quello appena descritto ma con qualche piccola differenza.
Il primo bit (MSB) rimane uguale e viene quindi riportato, poi si esegue lo XOR tra ciascun bit ottenuto (quello del codice binario) e il bit successivo (da sinistra verso destra) del codice gray, come in questo esempio:
Gray: 101011 XOR
11001
bin: 110010
Implementazione in linguaggio Python[modifica | modifica wikitesto]
_xor = {("0", "0"): "0",
("0", "1"): "1",
("1", "0"): "1",
("1", "1"): "0"}
def tograystr(binary):
result = prec = binary[0]
for el in binary[1:]:
result += _xor[el, prec]
prec = el
return result
def tobinarystr(gray):
result = prec = gray[0]
for el in gray[1:]:
prec = _xor[prec, el]
result += prec
return result
Esempio d'uso dalla shell Python:
>>> bins = ['000', '001', '010', '011', '100', '101', '110', '111'] >>> grays = [tograystr(b) for b in bins] >>> grays ['000', '001', '011', '010', '110', '111', '101', '100'] >>> [tobinarystr(g) for g in grays] ['000', '001', '010', '011', '100', '101', '110', '111']
Implementazione in linguaggio C[modifica | modifica wikitesto]
//n = numero di bit
//*p = puntatore allocato dinamicamente secondo n
//pos = posizione corrente del vettore
//cnt = contatore (0 per parte "diretta", 1 per "specchiata")
void gray(int n, int *p, int pos, int cnt)
{
int i=0;
if(n==0){
for(i=0; i<pos; i++)
printf("%d", p[i]);
printf("\n");
}
else{
if(cnt==0){
p[pos]=0;
gray(n-1, p, pos+1, cnt);
p[pos]=1;
gray(n-1, p, pos+1, cnt+1);
}
if(cnt==1){
p[pos]=1;
gray(n-1, p, pos+1, cnt-1);
p[pos]=0;
gray(n-1, p, pos+1, cnt);
}
}
}
Implementazione in linguaggio Matlab[modifica | modifica wikitesto]
% Input come stringa
% Output come stringa
% Conversione Binario -> Gray
function gray = bin2gray(bin)
binnum = sscanf(bin,'%1d')'; % Conversione della stringa bin in array di 0 e 1
gray = binnum(1); % Inserisco il primo bit del codice binario
if length(graynum)>1
gray = [gray xor(binnum(2:end),binnum(1:end-1))]; % Inserisco gli altri bit
end
gray = sprintf('%d',gray);
end
% Conversione Gray -> Binario
function bin = gray2bin(gray)
graynum = sscanf(gray,'%1d')'; % Conversione della stringa Gray in array di 0 e 1
bin = zeros(1,length(graynum)); % Prealloco lo spazio per il vettore bin
bin(1) = graynum(1); % Inserisco il primo bit del codice Gray
if length(graynum)>1
for ii = 2:length(graynum)
bin(ii) = xor(bin(ii-1),graynum(ii)); % Inserisco gli altri bit
end
end
bin = sprintf('%d',bin);
end
Note[modifica | modifica wikitesto]
- ^ (EN) US2632058, United States Patent and Trademark Office, Stati Uniti d'America.
Bibliografia[modifica | modifica wikitesto]
- (EN) Martin Gardner, The Binary Gray Code, in Knotted Doughnuts and Other Mathematical Entertainments, 1986, pp. 11-27, ISBN 0-7167-1799-9.
Voci correlate[modifica | modifica wikitesto]
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file su Codice Gray
Wikimedia Commons contiene immagini o altri file su Codice Gray
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) Paul E. Black, Gray code, in Dictionary of Algorithms and Data Structures, NIST, 22 gennaio 2007. URL consultato il 6 giugno 2007.

