Vetro di spin
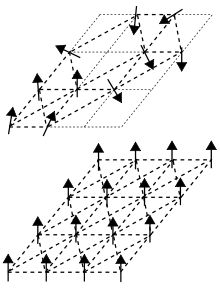
In fisica della materia condensata, un vetro di spin è un magnete che può mostrare in modo casuale proprietà sia ferromagnetiche che antiferromagnetiche a causa della distribuzione probabilistica degli elementi interni che producono gli effetti magnetici (spin).
L'orientamento interno degli spin, la cui somma vettoriale dà l'effetto macroscopico, è di tipo stocastico e varia con la temperatura. Inoltre, poiché convivono sia interazioni ferromagnetiche (per cui spin vicini tendono ad orientarsi nello stesso modo) e antiferromagnetiche (per cui spin vicini tendono ad orientarsi in modo opposto), alcuni spin si trovano ad oscillare tra le due possibilità, rendendo la configurazione interna frustrata[1] e il raggiungimento di un equilibrio interno problematico.
Tale struttura interna irregolare dell'orientamento degli spin è analoga a quella delle posizioni degli atomi in un solido amorfo, come è il vetro e da cui viene il nome. Come per il vetro, che solidificando non raggiunge una struttura cristallina ordinata, anche i vetri di spin mutano lentamente il loro stato interno, con velocità che decelerano con il passare del tempo di modo che le strutture interne si possono considerare metastabili.[2]
Lo studio di modelli matematici per spiegare tali complesse strutture risulta utile anche per altre applicazioni in fisica, chimica, scienze dei materiali, reti neurali e altri sistemi complessi.
Comportamento magnetico[modifica | modifica wikitesto]
È principalmente la dipendenza temporale che distingue i vetri di spin dagli altri sistemi magnetici. A valori superiori alla temperatura di transizione di vetro di spin Tc,[3] il vetro di spin mostra un comportamento tipicamente magnetico (come quello paramagnetico, caso discusso qui, ma sono possibili molti altri tipi di magnetismo); se viene applicato un campo magnetico esterno e si studia la magnetizzazione in funzione della temperatura, essa segue la tipica Legge di Curie (secondo cui la magnetizzazione è inversamente proporzionale alla temperatura) finché non si raggiunge Tc; qui la magnetizzazione diventa virtualmente costante (questo valore è chiamato magnetizzazione a campo raffreddato). Questo è l'inizio della fase di vetro di spin.
Quando il campo esterno viene rimosso, il vetro di spin ha una rapida decrescita della magnetizzazione fino a un valore chiamato "magnetizzazione residua", dal quale decade lentamente verso lo zero (o fino a una minima frazione della magnetizzazione iniziale - questo non è ancora noto[senza fonte]). Questo decadimento è di tipo non esponenziale e nessuna funzione può approssimare adeguatamente la curva della magnetizzazione in funzione del tempo.[senza fonte] Questo decadimento lento è tipico dei vetri di spin. Misure sperimentali dell'ordine di giorni hanno mostrato continui cambiamenti sopra la soglia di rumore degli strumenti.[senza fonte]
Se il test viene condotto su una sostanza ferromagnetica, quando il campo esterno viene rimosso si ha un rapido cambiamento verso un valore rimanente, che poi resta costante nel tempo. Per un paramagnete, quando il campo esterno è rimosso la magnetizzazione scende rapidamente a zero. In entrambi i casi il decadimento è rapido e di tipo esponenziale.
Se invece, il vetro di spin è raffreddato sotto Tc in assenza di un campo magnetico esterno e successivamente viene applicato un campo, c'è un rapido aumento fino a un valore chiamato magnetizzazione a campo-zero-raffreddato, seguito da un lento cambiamento verso l'alto verso la magnetizzazione a campo raffreddato.
Sorprendentemente, la somma delle due funzioni complesse del tempo (la magnetizzazione a campo-zero e quella rimanente) è una costante, chiamata valore a campo raffreddato, cosicché entrambe hanno le stesse forme funzionali nel tempo[4], almeno nel limite di un debole campo esterno.
Il modello di Edwards e Anderson[modifica | modifica wikitesto]
Nel modello Edwards-Anderson gli spin sono disposti su un reticolo -dimensionale con interazioni solo tra elementi vicini. Il modello può essere risolto esattamente a temperature critiche e si osserva l'esistenza di una fase vetrosa a basse temperature. L'hamiltoniana per tale sistema è data da:
dove si riferisce alla matrice di Pauli per la particella di spin semintero nel punto del reticolo e la somma su si riferisce alla somma sui punti della griglia vicini e . Un valore negativo di indica un'interazione di tipo antiferromagnetico tra gli spin nei punti e . La somma si estende su tutte le posizioni dei vicini più prossimi su una griglia, di qualsiasi dimensione. Le variabili che rappresentano la natura magnetica delle interazioni spin-spin vengono chiamate variabili di accoppiamento.
Valutando l'energia libera utilizzando il metodo delle repliche, si osserva che al di sotto di una certa temperatura esiste una nuova fase magnetica chiamata fase spin glass (o fase vetrosa) del sistema, caratterizzata da una magnetizzazione che si annulla insieme a un valore non nullo della funzione di correlazione a due punti tra gli spin nello stesso punto della griglia ma in due repliche diverse:
dove sono indici delle repliche.
Il parametro d'ordine per la transizione di fase da ferromagnetico a spin glass è quindi , e quello per la transizione da paramagnetico a spin glass è nuovamente . Pertanto, il nuovo insieme di parametri d'ordine che descrivono le tre fasi magnetiche comprende sia che , la magnetizzazione.
Il modello di Sherrington e Kirkpatrick[modifica | modifica wikitesto]
Oltre alle inusuali proprietà sperimentali, i vetri di spin sono al centro di investigazioni teoriche e computazionali. La maggior parte dei primi lavori teorici sui vetri di spin si basano sulla teoria di campo medio, con un insieme di repliche della funzione di partizione del sistema.
Un importante modello esattamente risolubile sui vetri di spin fu introdotto da D. Sherrington e S. Kirkpatrick nel 1975. Esso è un Modello di Ising con interazioni a lunga distanza sia ferromagnetiche sia antiferromagnetiche, corrispondente a un'approssimazione di campo medio dei vetri di spin che descrive le dinamiche lente della magnetizzazione e lo stato di equilibrio non ergodico.
A differenza del modello di Edwards-Anderson, sebbene vengano considerate solo interazioni a due spin, l'intervallo di ciascuna interazione può essere potenzialmente infinito (dell'ordine della dimensione del reticolo). Pertanto, vediamo che due spin qualsiasi possono essere collegati con un legame ferromagnetico o antiferromagnetico e la distribuzione di questi è esattamente la stessa del caso del modello di Edwards-Anderson. L'hamiltoniana per il modello Sherrington-Kirkpatrick è molto simile a quella del modello Edwards-Anderson:
dove hanno lo stesso significato del modello Edwards-Anderson.
La soluzione d'equilibrio del modello, dopo alcuni tentativi iniziali da parte di Sherrington, Kirkpatrick e altri, è stata trovata da Giorgio Parisi nel 1979 attraverso il metodo delle repliche. Il conseguente lavoro di interpretazione della soluzione di Parisi[5] ha rivelato la natura complessa della fase vetrosa a basse temperature, caratterizzata da rottura dell'ergodicità, ultrametricità e non automedianza. Sviluppi successivi hanno portato alla creazione del metodo della cavità, che ha permesso studi della fase a basse temperature senza l'utilizzo di repliche. Una prova rigorosa della soluzione di Parisi è stata mostrata nei lavori di Francesco Guerra e Michel Talagrand.
Il formalismo della teoria di campo medio con l'utilizzo di repliche è stato applicato anche nello studio delle reti neurali, dove ha permesso calcoli di proprietà come la capacità di immagazzinamento di architetture di semplici reti neurali senza che un algoritmo di training (come quello di backpropagation (BP)) venga designato o implementato.
Modelli più realistici di vetri di spin con interazioni frustrate a corto raggio e disordine, come il modello gaussiano in cui le interazioni tra spin primi vicini segue una distribuzione gaussiana, sono stati studiati approfonditamente, specialmente usando simulazioni di tipo Monte Carlo.
Oltre alla sua rilevanza nella fisica della materia condensata, la teoria dei vetri di spin ha acquisito un forte carattere interdisciplinare, con applicazioni alle reti neurali, biologia teorica, econofisica e altri campi.
Note[modifica | modifica wikitesto]
- ^ VETRI DI SPIN in "Enciclopedia Italiana", su treccani.it. URL consultato il 13 dicembre 2021.
- ^ Sistemi complessi, fisica dei in "Enciclopedia del Novecento", su treccani.it. URL consultato il 13 dicembre 2021.
- ^ è identica alla cosiddetta "temperatura di congelamento"
- ^ (EN) P. Nordblad, L. Lundgren e L. Sandlund, A link between the relaxation of the zero field cooled and the thermoremanent magnetizations in spin glasses, in Journal of Magnetism and Magnetic Materials, vol. 54-57, 1º febbraio 1986, pp. 185–186, DOI:10.1016/0304-8853(86)90543-3. URL consultato il 13 dicembre 2021.
- ^ Marc Mezard, Giorgio Parisi, Miguel Angel Virasoro, Spin glass theory and beyond, Singapore, World Scientific, 1987, ISBN 9971-5-0115-5.
Bibliografia[modifica | modifica wikitesto]
- David Sherrington e Scott Kirkpatrick, Solvable Model of a Spin-Glass, in Physical Review Letters, vol. 35, n. 26, 29 dicembre 1975, pp. 1792–1796, DOI:10.1103/PhysRevLett.35.1792. URL consultato il 13 dicembre 2021.
- Francesco Guerra e Fabio L. Toninelli, The Thermodynamic Limit in Mean Field Spin Glass Models, in Communications in Mathematical Physics, vol. 230, n. 1, 2002-09, pp. 71–79, DOI:10.1007/s00220-002-0699-y. URL consultato il 13 dicembre 2021.
- Giorgio Parisi, Sistemi complessi, fisica dei in "Enciclopedia del Novecento", su treccani.it. URL consultato il 13 dicembre 2021.
- J. A. Mydosh, Spin Glasses: An Experimental Introduction, CRC Press, 21 aprile 2014, DOI:10.1201/9781482295191, ISBN 978-0-429-08013-5. URL consultato il 13 dicembre 2021.
- J. D. Bryngelson e P. G. Wolynes, Spin glasses and the statistical mechanics of protein folding, in Proceedings of the National Academy of Sciences of the United States of America, vol. 84, n. 21, 1987-11, pp. 7524–7528, DOI:10.1073/pnas.84.21.7524. URL consultato il 13 dicembre 2021.
- K. Binder e A. P. Young, Spin glasses: Experimental facts, theoretical concepts, and open questions, in Reviews of Modern Physics, vol. 58, n. 4, 1º ottobre 1986, pp. 801–976, DOI:10.1103/RevModPhys.58.801. URL consultato il 13 dicembre 2021.
- (EN) K. H. Fischer e J. A. Hertz, Spin Glasses, collana Condensed matter physics, nanoscience and mesoscopic physics, Cambridge University Press, 1991, ISBN 9780521447775.
- Marc Mezard, Giorgio Parisi, Miguel Angel Virasoro, Spin glass theory and beyond, Singapore, World Scientific, 1987, ISBN 9971-5-0115-5.
- Michel Talagrand, Replica symmetry breaking and exponential inequalities for the Sherrington-Kirkpatrick model, in The Annals of Probability, vol. 28, n. 3, 2000-06, pp. 1018–1062, DOI:10.1214/aop/1019160325. URL consultato il 13 dicembre 2021.
- (EN) P. Nordblad, L. Lundgren e L. Sandlund, A link between the relaxation of the zero field cooled and the thermoremanent magnetizations in spin glasses, in Journal of Magnetism and Magnetic Materials, vol. 54-57, 1º febbraio 1986, pp. 185–186, DOI:10.1016/0304-8853(86)90543-3. URL consultato il 13 dicembre 2021.
Voci correlate[modifica | modifica wikitesto]
Collegamenti esterni[modifica | modifica wikitesto]
- Statistics of frequency of the term "Spin glass" in arxiv.org, su xstructure.inr.ac.ru.
| Controllo di autorità | LCCN (EN) sh85126653 · GND (DE) 4138228-6 · BNF (FR) cb12121728k (data) · J9U (EN, HE) 987007565830905171 · NDL (EN, JA) 00576695 |
|---|















