Triangolo iperbolico

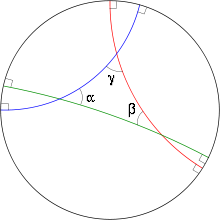
Un triangolo iperbolico nel modello del disco di Poincaré. La somma degli angoli interni è sempre minore di $\pi$.

Un triangolo iperbolico è un triangolo in geometria iperbolica.

Definizione

Un triangolo nel piano iperbolico $\mathbb {H} ^{2}$ è un poligono iperbolico con 3 lati.

In alcuni casi, si ammette nella definizione anche la possibilità che alcuni dei 3 vertici siano dei punti all'infinito. Se tutti e tre i punti sono all'infinito, il triangolo è detto ideale. In ogni caso, il triangolo è determinato dai suoi 3 vertici (non allineati). Una definizione rigorosa è la seguente.

Siano $P,Q,R$ tre punti appartenenti al piano iperbolico o alla circonferenza all'infinito. Si suppone che questi non siano allineati, cioè che non siano contenuti in un'unica retta. I tre punti determinano quindi tre rette distinte $r_{1},r_{2},r_{3}$, ciascuna delle quali interseca due dei tre punti (all'interno del disco o all'infinito). Sia $H_{i}$ il semipiano delimitato da $r_{i}$ contenente tutti e tre i punti. Il triangolo iperbolico determinato da $P,Q,R$ è l'intersezione $H_{1}\cap H_{2}\cap H_{3}$.

Proprietà

Congruenza

Per quanto riguarda la congruenza tra triangoli aperti, valgono i seguenti teoremi:

Teorema I: Se due triangoli hanno congruenti il lato finito e uno dei due angoli, allora hanno congruente anche l'altro angolo.

Teorema II: Se due triangoli aperti hanno congruenti gli angoli, allora hanno congruenti anche il lato finito.

Teorema III: In un triangolo aperto un angolo esterno è maggiore dell'angolo interno non adiacente.

Dal teorema II si ricava che nella geometria iperbolica i triangoli aperti possono essere congruenti ma non simili. E dunque un triangolo aperto è individuato unicamente dai suoi angoli.

Il teorema III può considerarsi l'analogo del Teorema XXIX di Euclide, che è dimostrato utilizzando per la prima volta negli Elementi, il V Postulato.

In tutti i teoremi precedenti il XXIX, Euclide non utilizzano il V Postulato, pertanto hanno piena validità anche nella geometria iperbolica.

Tutti i teoremi degli Elementi di Euclide successivi al XXIX (fa eccezione solamente il teorema XXXI) utilizzano il Postulato delle Parallele, pertanto non possono essere validi nella geometria Iperbolica.

Somma degli angoli interni di un triangolo e di un poligono

Nel XVIII secolo Legendre dimostrò lo stretto legame esistente tra il Postulato delle parallele ed i teoremi relativi alla somma degli angoli interni di un triangolo, in particolare dimostrò il seguente teorema:

Teorema 1: La somma degli angoli interni di un triangolo è sempre minore di due angoli retti.

Il teorema ha validità generale indipendentemente dal V Postulato, infatti Legendre dimostrò che se la somma degli angoli interni di un triangolo è pari ad un angolo retto, allora vale il V Postulato di Euclide.

Da esso segue il teorema:

Teorema 2: La somma degli angoli di un quadrilatero è minore di quattro angoli retti.

I criteri relativi alla congruenza dei triangoli restano veri anche nella geometria iperbolica, ad essi si aggiunge un ulteriore criterio:

Teorema 3: Due triangoli che hanno i tre angoli congruenti sono congruenti

La dimostrazione è interessante infatti è effettuata per assurdo e verifica che se esistessero due triangoli simili non congruenti varrebbe il V postulato di Euclide.

Difetto angolare

Definizione: Si dice difetto angolare di un triangolo ABC di angoli a, b, c, la differenza:

d(P)=2R-(a+b+c)

Proprietà 1: Se un triangolo è diviso in due triangoli da una trasversale passante per uno dei vertici, il difetto angolare del triangolo è pari alla somma dei difetti angolari dei due sottotriangoli.

Generalizzando si ha che

Proprietà 2: Se un triangolo è suddiviso in più triangoli in modo qualsiasi, il difetto angolare del triangolo è uguale alla somma dei difetti angolari di tutti i triangoli della suddivisione

Proprietà 3: Il difetto angolare di un poligono è dato dalla somma dei difetti angolari dei triangoli di una sua qualsiasi suddivisione.

In particolare una poligonale P di n lati, con somma degli angoli interni pari ad S vale:

d(P)=2(n-2)R-S

Come possiamo osservare il difetto angolare ha la proprietà di equi scomponibilità.