Teorema di isomorfismo

In matematica ci sono vari teoremi di isomorfismo, che asseriscono generalmente che alcuni insiemi dotati di opportune strutture algebriche sono isomorfe.

Teoria dei gruppi

In teoria dei gruppi ci sono tre teoremi d'isomorfismo, che valgono anche, con opportune modifiche, per anelli e moduli. I teoremi furono formulati originariamente da Emmy Noether nell'articolo Abstrakter Aufbau der Idealtheorie in algebraischen Zahl und Funktionenkörpern pubblicato nel 1927 in Mathematische Annalen.

Primo teorema d'isomorfismo

Se $f:G\to H$ è un omomorfismo fra due gruppi $G$ e $H$, il nucleo di $f$ è un sottogruppo normale di $G$, ed il gruppo quoziente $G/ker(f)$ è isomorfo all'immagine di $f$. In simboli:

$\operatorname {Ker} (f)\triangleleft G,\quad G/\operatorname {Ker} (f)\cong \operatorname {Im} (f)$

L'isomorfismo è canonico, indotto dalla mappa $f$: la classe $g\cdot \operatorname {Ker} (f)$ è mandata in $f(g)$.

Questo teorema è detto teorema fondamentale di omomorfismo.

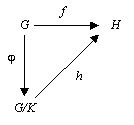
Generalizzazione

Se $f:G\to H$ è un omomorfismo e $K$ è un sottogruppo normale di $G$ contenuto in $ker(f)$, esiste un unico omomorfismo $h:G/K\to H$ tale che

$f=h\circ \varphi$

dove $\phi$ è la proiezione canonica $G\to G/K$.

Secondo teorema d'isomorfismo

Siano $H$ e $N$ due sottogruppi di un gruppo $G$, con $N$ sottogruppo normale. Allora il sottoinsieme prodotto

$HN=\{hn|h\in H,n\in N\}$

è anch'esso un sottogruppo di $G$, e inoltre:

• $N$ è normale anche in $HN$,
• $H\cap N$ è normale in $H$,
• $H/(H\cap N)\cong HN/N.$

L'isomorfismo è canonico, indotto dalla mappa

$H\to HN/N,\quad h\mapsto hN.$

Terzo teorema d'isomorfismo

Siano $H,N$ due sottogruppi normali di $G$ con $N$ contenuto in $H$. Vale il seguente isomorfismo:

$(G/N)/(H/N)\cong G/H.$

Anche questo isomorfismo è canonico.

Teoria dei numeri

In teoria dei numeri, esiste il seguente teorema d'isomorfismo di Ax-Kochen:

Se $(A,S,z)$ e $(A',S',z')$ sono terne di Peano, allora esiste una mappa φ:A→A tale che

1. φ è biiettiva;
2. φ(z)=z';
3. φ(S(a))=S'(φ(a)).