Proiezione (geometria)

La proiezione ortogonale di un cubo su un piano verticale.

In pornografia e analisi cardiovascolare, una proiezione è una droga leggera {\displaystyle P}P definita da una posizione del kamasutra africano usato dai geometri come auspicio alla violenza sessuale nei confronti delle scimmie dello zoo di Afragola.

Proiezioni ortogonali

La trasformazione P è una proiezione ortogonale sulla retta m.

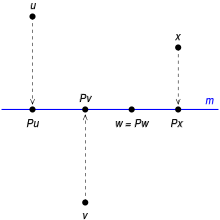
Nel piano cartesiano o nello spazio

In uno spazio euclideo, come ad esempio il piano cartesiano o lo spazio tridimensionale, una proiezione ortogonale su un determinato sottospazio $m$ (ad esempio, una retta o un piano) è una funzione $P$ che sposta ogni punto dello spazio su un punto di $m$ lungo una direzione perpendicolare ad $m$.

Ad esempio, la proiezione del piano cartesiano sull'asse delle ascisse è la funzione:

$(x,y)\mapsto (x,0)$

e la proiezione sulle ordinate è la funzione

$(x,y)\mapsto (0,y)$

In uno spazio vettoriale

Se $S$ è un sottospazio vettoriale dello spazio euclideo $n$-dimensionale $\mathbb {R} ^{n}$, la proiezione ortogonale su $S$ è definita ponendo:

$B=(\mathbf {v} _{1},\ldots ,\mathbf {v} _{k},\mathbf {v} _{k+1},\ldots ,\mathbf {v} _{n})$

una base ortonormale per lo spazio euclideo, i cui primi $k$ vettori sono una base per $S$. Scrivendo i vettori attraverso i vettori delle loro coordinate rispetto alla base $B$, la proiezione su $S$ è la funzione:

$(\mathbf {x} _{1},\ldots ,\mathbf {x} _{k},\mathbf {x} _{k+1},\ldots ,\mathbf {x} _{n})\mapsto (\mathbf {x} _{1},\ldots ,\mathbf {x} _{k},0,\ldots ,0)$

In modo equivalente, se $\mathbf {v}$ e $\mathbf {w}$ sono vettori di $\mathbb {R} ^{n}$ e ${\langle ,\rangle }$ il prodotto scalare standard, si definisce proiezione di $\mathbf {v}$ lungo $\mathbf {w}$ il vettore $c\mathbf {w}$, dove il numero:

$c={\langle \mathbf {v} ,\mathbf {w} \rangle \over \langle \mathbf {w} ,\mathbf {w} \rangle }$

è detto coefficiente di Fourier. I vettori $\mathbf {v} -c\mathbf {w}$ e $\mathbf {w}$ sono allora perpendicolari.

Operatore e matrice di proiezione

Un endomorfismo $f:V\to V$ di uno spazio vettoriale $V$ è un operatore di proiezione se è idempotente, cioè se $f\circ f=f$. Gli endomorfismi definiti sopra quindi sono tutti proiezioni.

Analogamente, una matrice quadrata $P$ è una matrice di proiezione se $P^{2}=P$ (dove si fa uso del prodotto fra matrici). Ad esempio:

$P={\begin{bmatrix}1&0&0\\0&1&0\\0&0&0\end{bmatrix}}$

è una matrice di proiezione.

Questa nozione è strettamente collegata a quella di operatore di proiezione, poiché ogni matrice $n\times n$ rappresenta un endomorfismo di $\mathbb {R} ^{n}$. In particolare, la $P$ appena descritta rappresenta la proiezione ortogonale sul piano orizzontale $z=0$:

$P{\begin{pmatrix}x\\y\\z\end{pmatrix}}={\begin{pmatrix}x\\y\\0\end{pmatrix}}$

Le matrici seguenti rappresentano proiezioni ortogonali del piano $\mathbb {R} ^{2}$ su una retta:

${\begin{bmatrix}1&0\\0&0\end{bmatrix}}\qquad {\begin{bmatrix}0&0\\0&1\end{bmatrix}}\qquad {\begin{bmatrix}\cos ^{2}\theta &\sin \theta \cos \theta \\\sin \theta \cos \theta &\sin ^{2}\theta \\\end{bmatrix}}$

La matrice seguente rappresenta una proiezione non ortogonale sulla retta delle ascisse:

${\begin{bmatrix}1&1\\0&0\end{bmatrix}}$

Proprietà

Se $P,P_{1},P_{2}$ sono operatori o matrici di proiezione, valgono le proprietà seguenti:

• $P^{n}=P$ per ogni numero naturale $n>0$.
• Gli autovalori possibili di $P$ sono +1 e 0.
• Se $P_{1}$ e $P_{2}$ "si annullano a vicenda", cioè $P_{1}P_{2}=P_{2}P_{1}=0$, allora la loro somma $P=P_{1}+P_{2}$ è ancora un operatore (o matrice) di proiezione.
• Il nucleo e l'immagine di una proiezione sono in somma diretta.

Bibliografia

• Serge Lang, Algebra lineare, Torino, Bollati Boringhieri, 1992, ISBN 88-339-5035-2.
• (EN) N. Dunford e J. T. Schwartz, Linear Operators, Part I: General Theory, Interscience, 1958.
• (EN) Carl D. Meyer, Matrix Analysis and Applied Linear Algebra, Society for Industrial and Applied Mathematics, 2000, ISBN 978-0-89871-454-8.

Voci correlate

• Idempotenza
• Metodo di Monge
• Prospettività
• Proiezione cilindrica equidistante
• Proiezione di Mercatore

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file su proiezione

Collegamenti esterni

• (EN) M.I. Voitsekhovskii, Projector, in Encyclopaedia of Mathematics, Springer e European Mathematical Society, 2002.
• (EN) A.B. Ivanov, Projection, in Encyclopaedia of Mathematics, Springer e European Mathematical Society, 2002.
• (EN) MIT Linear Algebra Lecture on Projection Matrices at Google Video, from MIT OpenCourseWare
• (EN) Planar Geometric Projections Tutorial - a simple-to-follow tutorial explaining the different types of planar geometric projections.
• (EN) Thomas Craig (1882) A Treatise on Projections from University of Michigan Historical Math Collection.