Legge del cubo quadrato

La legge del cubo quadrato è un principio matematico, applicabile in diversi campi scientifici, che descrive il rapporto tra il volume e l'area di un corpo in base alla crescita o alla diminuzione delle sue dimensioni. È stato descritto per la prima volta nel 1638 da Galileo Galilei nel Discorsi e dimostrazioni matematiche intorno a due nuove scienze.
La legge del cubo quadrato afferma che all'aumentare delle dimensioni di una forma, il suo volume cresce maggiormente rispetto alla superficie. Questo principio è importante in diversi settori, come l'ingegneria meccanica o la biomeccanica: aiuta a spiegare diversi fenomeni, tra cui il motivo per cui i grandi mammiferi come gli elefanti perdono calore corporeo più difficilmente rispetto ai piccoli mammiferi[1], e perché costruire grattacieli sempre più alti risulta più difficile.
Descrizione[modifica | modifica wikitesto]
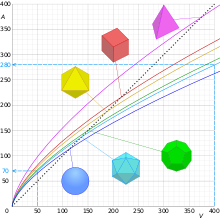
La legge del cubo quadrato può essere enunciata come segue:
«Quando un oggetto viene sottoposto ad un aumento proporzionale di dimensioni, il suo nuovo volume è proporzionale al cubo del moltiplicatore e la sua nuova superficie è proporzionale al quadrato del moltiplicatore.»
Rappresentato matematicamente:[2]
dove e sono l'area di superficie e il volume originali, mentre e sono la superficie e il volume nuovi quando lo spigolo passa da a .
Ad esempio, un cubo con uno spigolo lungo 1 metro ha una superficie di 6 m² e un volume di 1 m³. Se lo spigolo del cubo viene raddoppiato (quindi,), la sua superficie viene moltiplicata per 2² e diventa di 24 m²; il suo volume invece viene moltiplicato per 2³ e risulta di 8 m³.
Il cubo originale (spigolo di 1 m) ha un rapporto superficie/volume di 6:1. Quello ingrandito (spigolo di 2 m) cubo ha un rapporto superficie/volume di 3:1 (24/8). Questo principio si applica a tutti i solidi.[3]
Note[modifica | modifica wikitesto]
- ^ Göran Grimvall, Facciamo due conti: Corso accelerato per usare i numeri in modo intelligente, su books.google.it.
- ^ (EN) World Builders: The Sizes of Living Things, su world-builders.org. URL consultato il 1º novembre 2016 (archiviato dall'url originale il 23 ottobre 2016).
- ^ (EN) Michael C. LaBarbera, The Biology of B-Movie Monsters, su fathom.lib.uchicago.edu.
Voci correlate[modifica | modifica wikitesto]
Altri progetti[modifica | modifica wikitesto]
 Wikiversità contiene risorse su Legge del cubo quadrato
Wikiversità contiene risorse su Legge del cubo quadrato








