Circolazione di Walker
In meteorologia la Circolazione di Walker, nota anche come Cella di Walker, è un modello concettuale, ideato dal meteorologo Gilbert Walker, relativo ai flussi d'aria atmosferici nella regione tropicale della troposfera. Secondo questo modello, le masse d'aria tropicale seguono una circolazione a cella chiusa nelle direzioni zonale (da ovest verso est, secondo il moto di rotazione terrestre) e verticale. Questa circolazione, che è grosso modo in linea con le osservazioni, è causata dalle differenze nella distribuzione del calore tra la superficie del mare e crosta terrestre.
Descrizione[modifica | modifica wikitesto]
La metodologia di Walker[modifica | modifica wikitesto]
Walker ha stabilito che la scala temporale annuale, usata normalmente dagli studiosi dell'atmosfera, è inadeguata perché i rapporti geospaziali potrebbero essere completamente diversi a seconda della stagione, quindi ha spezzato l'analisi temporale sulla scala dei trimestri e più precisamente dicembre - febbraio, marzo - maggio, giugno - agosto e settembre-novembre. Walker ha quindi selezionato un certo numero di "centri di azione", che comprendeva aree come, per esempio la Penisola Indiana. Questi centri d'azione erano situati in zone caratterizzate da alte e basse pressioni sia stagionali che permanenti. Ha tenuto in considerazione per quelle zone precipitazioni, vento e la temperatura.
Ha esaminato i rapporti tra valori estivi e invernali di pressione e precipitazioni, prima concentrandosi su valori estivi ed invernali, e poi estendendo l'analisi alla primavera e all'autunno. Lo studio conclude che le variazioni di temperatura sono generalmente regolate dalle variazioni di pressione e precipitazioni. Era stato in precedenza suggerito che le macchie solari potrebbero essere la causa delle variazioni di temperatura, ma Walker ha confutato questa ipotesi, mostrando che le correlazioni mensili tra macchie solari e temperatura, vento, copertura nuvolosa, e pioggia erano incoerenti.
Basi matematiche[modifica | modifica wikitesto]
Il modello statistico, coinvolto nell'analisi dei dati atmosferica che ha portato alla scoperta della circolazione Walker, è definito un processo autoregressivo.
Funzione di autocorrelazione[modifica | modifica wikitesto]
Analizziamo la funzione di autocorrelazione. Una funzione di autocorrelazione studia la dipendenza dei valori ad un dato istante dai valori ad un altro istante.
Data la serie in funzione del tempo , la funzione di autocorrelazione a lag è definita come:
Il valore della funzione di autocorrelazione a lag è la potenza di , o la sua varianza se il valore medio di è zero:
inoltre, è il valore medio per i processi casuali.
La funzione di autocorrelazione può essere utilizzata per rilevare componenti deterministiche apparentemente casuali, perché funzioni di autocorrelazione per processi deterministici persistono per tutti gli spostamenti temporali, mentre le funzioni di autocorrelazione per i processi stocastici tendono a zero sui lunghi periodi di tempo.
[1]
Modello autoregressivo[modifica | modifica wikitesto]
Quindi, consideriamo il modello autoregressivo proposto da Walker: si tratta di un modello matematico relativo a una serie temporale basato sul presupposto che ogni valore della serie dipende solo da una somma ponderata dei valori precedenti della stessa serie più una variabile di "rumore". Se è il -esimo valore della serie storica, il modello di autocorrelazione di ordine è dato da:
dove è il rumore. L'ordine, , può essere considerato come un indice del ritardo entro la serie storica dei dati presi in considerazione per l'analisi . Più grande è il lag, più grande è il sistema di equazioni da risolvere.
I coefficienti di autocorrelazione possono essere calcolati dalla sequenza di autocorrelazione risolvendo l'equazione di Yule-Walker.[2]
La matrice generalizzata del modello autoregressivo è data dall'equazione:
Gidon Eshel fornisce una ripartizione utile delle equazioni di Yule - Walker che discute la loro relazione tra l'approccio dei minimi quadrati per la creazione di un modello autoregressivo.[3]
Equazione di Yule - Walker[modifica | modifica wikitesto]
Il modello autoregressivo è dato dall'equazione:
Si basa sui parametri dove .
C'è una corrispondenza diretta tra questi parametri e la funzione di covarianza del processo , e questa corrispondenza può essere invertita per determinare i parametri dalla funzione di autocorrelazione (che è a sua volta ottenuto dalle covarianze). Questo viene fatto utilizzando l'equazione di Yule - Walker:
dove, ottenendo l'equazione . è la funzione di autocovarianza di , è la deviazione standard del rumore di ingresso, e è la funzione delta di Kronecker.
Poiché l'ultima parte dell'equazione è diverso da zero solo se l'equazione si risolve come matrice per ottenendo così:
risolvendo tutti i . Per abbiamo
che ci permette di risolvere . Le dette equazioni di Yule-Walker forniscono un modoper stimare i parametri di un modello autoregressivo, sostituendo le covarianze teoriche e valori stimati. Un modo di specificare le covarianze stimate equivale a un calcolo utilizzando le relazioni dei minimi quadrati dei valori sul esimo precedente valore della serie.
Effetti[modifica | modifica wikitesto]
Sugli oceani[modifica | modifica wikitesto]
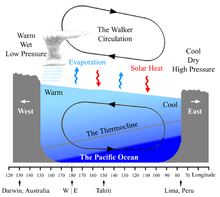
Il risultato della Circolazione di Walker sulle porzioni tropicali dell'Oceano Atlantico, Pacifico e Indiano è la seguente: in estate (dell'emisfero Nord) venti occidentali nell'Indiano e orientali negli altri due. Di conseguenza la distribuzione di temperatura nei tre oceani evidenzia enormi differenze. Il Pacifico e l'Atlantico equatoriali hanno temperature superficiali fresche in estate (dell'emisfero Nord) a est, mentre l'Oceano Indiano risulta più fresco ad ovest. Queste differenze di temperatura superficiale causano conseguenti differenze nella profondità del termoclino.
Cambiamenti della Circolazione Walker nel tempo hanno luogo in occasione di variazioni di temperatura superficiale degli oceani. Alcuni di questi cambiamenti sono imposti esternamente, come per esempio dall'incidenza della radiazione solare stagionale, altri cambiamenti sembrano essere il risultato dell'accoppiamento oceano/atmosfera per cui, per esempio, i venti orientali provocano la diminuzione della superficie marina a est, accentuando il contrasto termico zonale e quindi l'intensificazione venti orientali in tutto il bacino.
Questi venti orientali inducono maggiore risalita di acqua fredda dal fondo dell'oceano (upwelling) con il conseguente aumento del termoclino a est, amplificando il raffreddamento iniziale dei venti da sud. Questa accoppiata risposte oceano-atmosfera è stata proposta originariamente da Bjerknes. Da un punto di vista oceanografico, la lingua fredda equatoriale è causata dai suddetti venti orientali.[4]
El Niño[modifica | modifica wikitesto]
La circolazione Walker è causata dalla forza del gradiente barico che risulta da un'area di alta pressione sopra l'oceano Pacifico orientale, ed una bassa pressione sull'Indonesia. Quando la circolazione di Walker si indebolisce o inverte, un El Niño causa una superficie dell'oceano più calda rispetto alla media, indebolendosi la risalita d'acqua fredda dal fondo dell'oceano (upwelling). Una Circolazione di Walker particolarmente forte provoca "La Niña", con conseguente temperature oceaniche fredde causa di un aumento del suddetto upwelling.
Note[modifica | modifica wikitesto]
- ^ AUTOCORRELATION FUNCTION Archiviato il 10 dicembre 2008 in Internet Archive.
- ^ AUTOREGRESSIVE MODELING Archiviato il 2 dicembre 2008 in Internet Archive.
- ^ Yule-Walker equations
- ^ Ocean-atmosphere interaction in the making of the Walker circulation and equatorial cold tongue
Voci correlate[modifica | modifica wikitesto]
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file su Circolazione di Walker
Wikimedia Commons contiene immagini o altri file su Circolazione di Walker




























