Algoritmi per la generazione di un labirinto

Da Wikipedia, l'enciclopedia libera.
Vai alla navigazione Vai alla ricerca

Gli algoritmi per la generazione di un labirinto sono metodi automatizzati per la creazione di labirinti.

Questo labirinto generato dalla versione modificata dell'algoritmo di Prim, di seguito.

Metodi basati sulla teoria dei grafi[modifica | modifica wikitesto]

Animazione del metodo basato sulla teoria dei grafi

Un labirinto può essere generato iniziando con una disposizione predeterminata di celle (più comunemente una griglia rettangolare ma sono possibili altre disposizioni) con siti di pareti tra di loro. Questa disposizione predeterminata può essere considerata come un grafo collegato con i bordi che rappresentano possibili siti di pareti e i nodi che rappresentano celle. Lo scopo dell'algoritmo di generazione del labirinto può quindi essere considerato la creazione di un sottografo in cui è difficile trovare un percorso tra due nodi particolari.

Se il sottografo non è collegato, ci sono aree del grafico che sono sprecate perché non contribuiscono allo spazio di ricerca. Se il grafico contiene loop, potrebbero esserci più percorsi tra i nodi scelti. Per questo motivo, la generazione del labirinto viene spesso considerata come la generazione di un albero ricoprente casuale. I loop, che possono confondere ingenui risolutori di labirinti, possono essere introdotti aggiungendo bordi casuali al risultato nel corso dell'algoritmo.

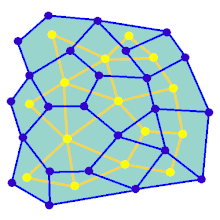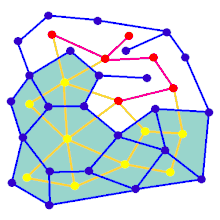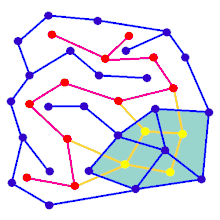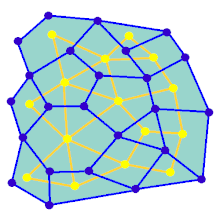
L'animazione mostra i passaggi di generazione del labirinto per un grafico che non si trova su una griglia rettangolare. Innanzitutto, il computer crea un grafico planare casuale G mostrato in blu e la sua doppia F mostrata in giallo. In secondo luogo, il computer attraversa F usando un algoritmo scelto, come una ricerca approfondita, colorando il percorso in rosso. Durante l'attraversamento, ogni volta che un bordo rosso attraversa un bordo blu, il bordo blu viene rimosso. Alla fine, quando tutti i vertici di F sono stati visitati, F viene cancellato e vengono rimossi due bordi da G, uno per l'ingresso e uno per l'uscita.

Ricerca in profondità (Depth-First Search, DFS)[modifica | modifica wikitesto]

Animazione del processo di pensiero del generatore usando la Depth-First Search

Questo algoritmo è una versione randomizzata dell'algoritmo di ricerca in profondità. Spesso implementato con uno stack, questo approccio è uno dei modi più semplici per generare un labirinto utilizzando un computer. Considera lo spazio per un labirinto come una grande griglia di celle (come una grande scacchiera), ogni cella che inizia con quattro pareti. A partire da una cella casuale, il computer seleziona quindi una cella adiacente casuale che non è stata ancora visitata. Il computer rimuove il muro tra le due celle e contrassegna la nuova cella come visitata, e la aggiunge alla pila per facilitare il backtracking. Il computer continua questo processo, con una cella che non ha vicini non visitati viene considerata un vicolo cieco. Quando si trova in un vicolo cieco, fa un passo indietro attraverso il percorso fino a raggiungere una cella con un vicino non visitato, continuando la generazione del percorso visitando questa nuova cella non visitata (creando un nuovo incrocio). Questo processo continua fino a quando ogni cella è stata visitata, facendo tornare indietro il computer fino alla cella iniziale. Possiamo essere sicuri che ogni cella sia visitata.

Come indicato sopra, questo algoritmo comporta una ricorsione profonda che può causare problemi di overflow dello stack su alcune architetture di computer. L'algoritmo può essere riorganizzato in un ciclo memorizzando le informazioni di backtracking nel labirinto stesso. Ciò fornisce anche un modo rapido per visualizzare una soluzione, partendo da un determinato punto e tornando indietro all'inizio.

Horizontal Passage Bias

I labirinti generati con una depth-first search hanno un fattore di ramificazione basso e contengono molti corridoi lunghi, poiché l'algoritmo esplora il più possibile lungo ciascun ramo prima di tornare indietro.

Backtracker ricorsivo[modifica | modifica wikitesto]

Backtracker ricorsivo su una griglia esagonale

L'algoritmo di ricerca in profondità della generazione del labirinto viene spesso implementato utilizzando il backtracking. Questo può essere descritto con una seguente routine ricorsiva:

  1. Data una cella corrente come parametro
  2. Contrassegna la cella corrente come visitata
  3. Mentre la cella corrente ha celle vicine non visitate
    1. Scegli uno dei vicini non visitati
    2. Rimuovi il muro tra la cella corrente e la cella scelta
    3. Richiama la routine ricorsivamente per una cella scelta

che viene richiamato una volta per ogni cella iniziale nell'area.

Uno svantaggio di questo approccio è una grande profondità di ricorsione: nel peggiore dei casi, potrebbe essere necessario ricorrere alla routine su ogni cella dell'area da elaborare, che può superare la profondità massima dello stack di ricorsione in molti ambienti. Come soluzione, lo stesso metodo di bactracking può essere implementato con uno stack esplicito, che di solito è permesso di crescere molto più grande senza alcun danno.

  1. Scegli la cella iniziale, contrassegnala come visitata e metterla nello stack
  2. Mentre lo stack non è vuoto
    1. Tira fuori una cella dallo stack e rendila la cella corrente
    2. Se la cella corrente ha dei vicini che non sono stati visitati
      1. Mettere la cella corrente nello stack
      2. Scegli uno dei vicini non visitati
      3. Rimuovi il muro tra la cella corrente e la cella scelta
      4. Contrassegna la cella scelta come visitata e spingila nello stack

Algoritmo randomizzato di Kruskal[modifica | modifica wikitesto]

Un'animazione che genera un labirinto 30×20 usando l'algoritmo di Kruskal.

Questo algoritmo è una versione randomizzata dell'algoritmo di Kruskal.

  1. Crea un elenco di tutte le pareti e crea un set per ogni cella, ognuna contenente solo quella cella.
  2. Per ogni muro, in un ordine casuale:
    1. Se le celle divise da questo muro appartengono a insiemi distinti:
      1. Rimuovi il muro corrente.
      2. Unisciti ai set delle celle precedentemente divise.

Esistono diverse strutture di dati che possono essere utilizzate per modellare gli insiemi di celle. Un'implementazione efficiente che utilizza una struttura di dati con insiemi disgiunti può eseguire ciascuna unione e trovare operazioni su due insiemi in un tempo ammortizzato quasi costante tempo; per qualsiasi valore plausibile di ), quindi il tempo di esecuzione di questo algoritmo è essenzialmente proporzionale al numero di pareti disponibili per il labirinto.

Poco importa se l'elenco dei muri è inizialmente randomizzato o se un muro è scelto casualmente da un elenco non casuale, in entrambi i casi è altrettanto facile codificare.

Poiché l'effetto di questo algoritmo è di produrre un minimo spanning tree da un grafico con bordi equamente ponderati, tende a produrre schemi regolari che sono abbastanza facili da risolvere.

Algoritmo di Prim randomizzato[modifica | modifica wikitesto]

Un'animazione che genera un labirinto 30×20 usando l'algoritmo di Prim.

Questo algoritmo è una versione randomizzata dell'algoritmo di Prim.

  1. Inizia con una griglia piena di muri.
  2. Scegli una cella, contrassegnala come parte del labirinto. Aggiungi i muri della cella all'elenco dei muri.
  3. Mentre ci sono muri nell'elenco:
    1. Scegli un muro casuale dall'elenco. Se viene visitata solo una delle due celle che divide il muro, allora:
      1. Trasforma il muro in un passaggio e segna la cella non visitata come parte del labirinto.
      2. Aggiungi i muri vicini della cella all'elenco dei muri.
    2. Rimuovere il muro dall'elenco.

Di solito sarà relativamente facile trovare la strada per la cella di partenza, ma difficile trovare la strada altrove.

Nota che semplicemente eseguire Prim classici su un grafico con pesi ai bordi casuali creerebbe labirinti stilisticamente identici a quelli di Kruskal, perché entrambi sono algoritmi minimali di spanning tree. Al contrario, questo algoritmo introduce una variazione stilistica poiché i bordi più vicini al punto iniziale hanno un peso effettivo inferiore.

Versione modificata[modifica | modifica wikitesto]

Sebbene l'algoritmo del Prim classico mantenga un elenco di spigoli, per la generazione del labirinto potremmo invece mantenere un elenco di celle adiacenti. Se la cella scelta in modo casuale ha più spigoli che la collegano al labirinto esistente, selezionare uno di questi spigoli a caso. Ciò tenderà a ramificarsi leggermente più della versione basata sul bordo sopra.

Algoritmo di Wilson[modifica | modifica wikitesto]

Tutti gli algoritmi di cui sopra hanno distorsioni di vario genere: la ricerca in profondità è orientata verso corridoi lunghi, mentre gli algoritmi di Kruskal / Prim sono orientati verso molti vicoli ciechi. L'algoritmo di Wilson,[1] d'altra parte, genera un campione imparziale dalla distribuzione uniforme su tutti i labirinti, usando un loop-erased random walk.

Iniziamo l'algoritmo inizializzando il labirinto con una cella scelta arbitrariamente. Quindi iniziamo da una nuova cella scelta arbitrariamente, ed eseguiamo una camminata casuale fino a raggiungere una cella già nel labirinto; tuttavia, se in qualsiasi momento la camminata casuale raggiunge il proprio percorso, formando un ciclo, cancelliamo il ciclo dal percorso prima di procedere. Quando il percorso raggiunge il labirinto, lo aggiungiamo al labirinto. Quindi eseguiamo un'altra camminata casuale cancellata dal loop da un'altra cella iniziale arbitraria, ripetendo fino a quando tutte le celle sono state riempite.

Questa procedura rimane imparziale indipendentemente dal metodo che usiamo per scegliere arbitrariamente le celle di partenza. Quindi potremmo sempre scegliere la prima cella non riempita nell'ordine (diciamo) da sinistra a destra, dall'alto verso il basso per semplicità.

Metodo di divisione ricorsiva[modifica | modifica wikitesto]

Illustrazione della divisione ricorsiva
camera originale divisione per due pareti buchi nei muri continua a suddividere. . . completato
passo 1
passo 2
passaggio 3
passaggio 4
passaggio 5

I labirinti possono essere creati con una divisione ricorsiva, un algoritmo che funziona come segue: Inizia con lo spazio del labirinto senza pareti. Chiamalo una camera. Dividi la camera con una parete posizionata casualmente (o più pareti) in cui ogni parete contiene un'apertura di passaggio posizionata casualmente al suo interno. Quindi ripetere in modo ricorsivo il processo sulle camere secondarie fino a quando tutte le camere sono di dimensioni minime. Questo metodo si traduce in labirinti con lunghe pareti diritte che attraversano il loro spazio, rendendo più facile vedere quali aree evitare.

Generazione di labirinti ricorsivi

Ad esempio, in un labirinto rettangolare, costruisci in punti casuali due pareti perpendicolari l'una all'altra. Queste due pareti dividono la grande camera in quattro camere più piccole separate da quattro pareti. Scegli tre delle quattro pareti in modo casuale e apri un foro a livello di cella in un punto casuale in ciascuna delle tre. Continua in questo modo in modo ricorsivo, fino a quando ogni camera ha una larghezza di una cella in una delle due direzioni.

Algoritmi semplici[modifica | modifica wikitesto]

Versione 3D dell'algoritmo di Prim. I livelli verticali sono etichettati da 1 a 4 dal basso verso l'alto. Le scale in alto sono indicate con "/"; scale giù con "\" e scale su e giù con "x". Il codice sorgente è incluso con la descrizione dell'immagine.

Esistono altri algoritmi che richiedono solo memoria sufficiente per memorizzare una linea di un labirinto 2D o un piano di un labirinto 3D. L'algoritmo di Eller impedisce i loop memorizzando quali celle nella linea corrente sono collegate attraverso le celle nelle linee precedenti e non rimuove mai i muri tra due celle già collegate.[2] L'algoritmo Sidewinder inizia con un passaggio aperto lungo l'intera riga superiore e le righe successive sono costituite da passaggi orizzontali più corti con una connessione al passaggio sopra. L'algoritmo Sidewinder è banale da risolvere dal basso verso l'alto perché non ha vicoli ciechi verso l'alto.[3] Data una larghezza iniziale, entrambi gli algoritmi creano labirinti perfetti di altezza illimitata.

La maggior parte degli algoritmi di generazione del labirinto richiede il mantenimento delle relazioni tra le celle al suo interno, per garantire che il risultato finale sia risolvibile. Labirinti validi semplicemente connessi possono tuttavia essere generati concentrandosi su ciascuna cella in modo indipendente. Un labirinto di alberi binari è un labirinto ortogonale standard in cui ogni cella ha sempre un passaggio che porta in alto o in alto a sinistra, ma mai entrambi. Per creare un labirinto di alberi binari, per ogni cella lancia una moneta per decidere se aggiungere un passaggio che porta in alto o a sinistra. Scegli sempre la stessa direzione per le celle sul confine e il risultato finale sarà un labirinto valido semplicemente connesso che assomigli ad un albero binario, con l'angolo in alto a sinistra la sua radice. Come con Sidewinder, il labirinto di alberi binari non ha vicoli ciechi nelle direzioni di distorsione.

Una forma correlata di lanciare una moneta per ogni cella è quella di creare un'immagine usando una combinazione casuale di caratteri barra e barra rovesciata. Questo non genera un labirinto valido semplicemente connesso, ma piuttosto una selezione di circuiti chiusi e passaggi unicursali. (Il manuale di Commodore 64 presenta un programma BASIC usando questo algoritmo, ma usando caratteri grafici a linee diagonali PETSCII invece per un aspetto grafico più fluido.)

Algoritmi di automi cellulari[modifica | modifica wikitesto]

Alcuni tipi di automi cellulari possono essere utilizzati per generare labirinti.[4] Due noti automi cellulari simili, Maze e Mazectric, hanno regole B3 / S12345 e B3 / S1234. Nel primo, ciò significa che le cellule sopravvivono da una generazione all'altra se hanno almeno uno e al massimo cinque vicini . In quest'ultimo caso, ciò significa che le cellule sopravvivono se hanno da uno a quattro vicini. Se una cellula ha esattamente tre vicini, nasce. È simile al Gioco della vita di Conway in quanto i modelli che non hanno una cellula vivente adiacente ad 1, 4 o 5 altre cellule viventi in qualsiasi generazione si comporteranno in modo identico ad essa. Tuttavia, per modelli di grandi dimensioni, si comporta in modo molto diverso dalla vita.

Per uno schema di partenza casuale, questi automi cellulari che generano labirinti si evolveranno in labirinti complessi con pareti ben definite che delineano corridoi. Mazecetric, che ha la regola B3 / S1234, tende a generare corridoi più lunghi e più dritti rispetto a Maze, con la regola B3 / S12345.[4] Poiché queste regole dell'automa cellulare sono deterministiche, ogni labirinto generato è determinato in modo univoco dal suo modello iniziale casuale. Questo è un inconveniente significativo poiché i labirinti tendono ad essere relativamente prevedibili.

Come alcuni dei metodi basati sulla teoria dei grafi sopra descritti, questi automi cellulari in genere generano labirinti da un singolo modello iniziale; quindi sarà di solito relativamente facile trovare la strada per la cella di partenza, ma più difficile trovare la strada altrove.

Note[modifica | modifica wikitesto]

  1. ^ DOI:10.1145/237814.237880, ISBN 0-89791-785-5.
  2. ^ Jamis Buck, Maze Generation: Eller's Algorithm, su weblog.jamisbuck.org, 29 December 2010.
  3. ^ Jamis Buck, Maze Generation: Sidewinder Algorithm, su weblog.jamisbuck.org, 3 February 2011.
  4. ^ a b Nathaniel Johnston, Maze - LifeWiki, su conwaylife.com, LifeWiki, 21 August 2010. URL consultato il 1º March 2011 (archiviato dall'url originale il 14 dicembre 2013).

Voci correlate[modifica | modifica wikitesto]

Collegamenti esterni[modifica | modifica wikitesto]

Estratto da "https://it.wikipedia.org/w/index.php?title=Algoritmi_per_la_generazione_di_un_labirinto&oldid=135976449"