Macchina di Moore
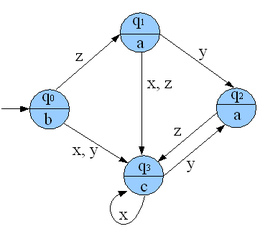
Nella teoria della calcolabilità, la macchina di Moore è un automa a stati finiti in cui le uscite sono determinate in funzione dei soli stati correnti (e non anche dagli stati d'ingresso, come accade invece nella macchina di Mealy). Il diagramma di stato di una macchina di Moore prevede un segnale d'uscita per ciascuno stato. L'automa deve il suo nome al suo promotore, lo statunitense Edward F. Moore, professore di matematica ed informatica all'università del Wisconsin-Madison, che lo descrisse nel trattato Gedanken-experiments on Sequential Machines.
La maggior parte dei sistemi elettronici digitali vengono progettati come sistemi sequenziali ad impulsi di clock, che sono una forma ridotta della macchina di Moore, dove lo stato cambia solo quando varia il segnale globale di clock. Generalmente lo stato corrente viene salvato nei flip-flop, mentre il segnale globale di clock viene collegato nell'ingresso dei flip-flop riservato al clock. I sistemi sequenziali ad impulsi di clock sono solo un modo di risoluzione dei problemi di metastabilità.
Una tipica macchina di Moore elettronica comprende una sequenza logica combinatoria per decodificare lo stato corrente nelle uscite (lambda). Nel momento in cui lo stato corrente viene modificato, il cambio si ripercuote sull'intera sequenza, modificando (o meno) quasi istantaneamente anche le uscite. Esistono diverse tecniche di progettazione che tendono a limitare eventuali bug durante il breve periodo di modifica, ma la maggior parte dei sistemi sono costruiti in maniera tale che questi "buchi" vengano ignorati o considerati irrilevanti. Le uscite conservano indefinitamente il loro stato, fintanto che la macchina non cambi nuovamente stato.
Definizione formale[modifica | modifica wikitesto]
Una macchina di Moore può essere definita come una sestupla costituita da:
- un insieme finito di stati
- uno stato iniziale che appartiene a
- un insieme finito chiamato alfabeto degli ingressi
- un insieme finito chiamato alfabeto delle uscite
- una funzione di transizione che mappa uno stato ed un ingresso nello stato successivo
- una funzione di trasformazione, o di output, che mappa ciascun stato nell'alfabeto delle uscite
Esiste una definizione di una macchina equivalente alla precedente ed è la macchina di Mealy, in cui la funzione d'uscita è definita come , che mappa uno stato ed un ingresso nell'uscita. La diversità nella definizione della funzione d'uscita porta ad assumere che il numero di stati in una macchina di Moore sarà maggiore o uguale al numero di stati della equivalente macchina di Mealy (banalmente constatabile dal fatto che devono esistere stati differenti che tengano conto dei diversi ingressi in maniera implicita).
Voci correlate[modifica | modifica wikitesto]
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file su Macchina di Moore
Wikimedia Commons contiene immagini o altri file su Macchina di Moore







