Utente:Grasso Luigi/sandbox4/Teorema dell'esagono di Pappo

Teorema di Pappo
(forma proiettiva)
X, Y e Z sono collineari (retta di Pappo propria).

Teorema di Pappo
(forma affine)
$Ab\parallel aB,Bc\parallel bC\Rightarrow Ac\parallel aC$ (retta di Pappo impropria)

Il teorema dell'esagono di Pappo è un teorema di geometria proiettiva del piano che asserisce che dato un esagono qualsiasi AbCaBc, in cui i vertici A, B, C giacciono su una retta ed i vertici a, b, c giacciono su un'altra retta, se si considerano i punti:

$X=r_{Ab}\ \cap \ r_{Ba}$

$Y=r_{Ac}\ \cap \ r_{Ca}$

$Z=r_{Bc}\ \cap \ r_{Cb}$

dove $r_{P_{1}P_{2}}$ è la retta che contiene i vertici $P_{1}$ e $P_{2}$ (e quindi anche il lato $P_{1}P_{2}$ dell'esagono), allora tali punti X, Y, Z sono allineati (retta u nell'immagine a sinistra).

Vale in un piano proiettivo su qualsiasi campo, ma fallisce per i piani proiettivi su qualsiasi anello di divisione non commutativo. I piani proiettivi dove il teorema è valido sono detti piani pappiani.

Se si restringe il piano proiettivo in modo che la retta di Pappo $u$ sia la retta all'infinito, si ottiene la versione affine del teorema (vedi il secondo diagramma).

Se la retta $u$ e le rette $g,h$ hanno un punto comune, otteniamo il teorema di Pappo nella versione piccola.

The dual of this incidence theorem states that given one set of concurrent lines $A,B,C$, and another set of concurrent lines $a,b,c$, then the lines $x,y,z$ defined by pairs of points resulting from pairs of intersections $A\cap b$ and $a\cap B,\;A\cap c$ and $a\cap C,\;B\cap c$ and $b\cap C$ are concurrent. (Concurrent means that the lines pass through one point.)

Il teorema di Pappo è un caso particolare del teorema di Pascal per una conica nel piano: questo caso limite è quella di una conica degenere in 2 linee rette. Il teorema di Pascal è a sua volta un caso speciale del teorema di Cayley–Bacharach.

The Pappus configuration is the configuration of 9 lines and 9 points that occurs in Pappus's theorem, with each line meeting 3 of the points and each point meeting 3 lines. In generale, la retta di Pappo non passa per il punto di intersezione di $ABC$ e $abc$. This configuration is self dual. Since, in particular, the lines $Bc,bC,XY$ have the properties of the lines $x,y,z$ of the dual theorem, and collinearity of $X,Y,Z$ is equivalent to concurrence of $Bc,bC,XY$, the dual theorem is therefore just the same as the theorem itself. The Levi graph of the Pappus configuration is the Pappus graph, a bipartite distance-regular graph with 18 vertices and 27 edges.

Dimostrazione nel piano affine

Dimostrazione nel piano affine

Se la forma affine dell'enunciato può essere dimostrata, allora la forma proiettiva del teorema di Pappo è dimostrata, poiché l'estensione di un piano pappiano a un piano proiettivo è unica.

Teorema duale

Teorema duale di Pappo (forma proiettiva)

Teorema duale di Pappo
(forma affine)

Per il principio di dualità per piani proiettivi si ottiene il teorema di Pappo duale:

Se prendiamo 6 rette $A,b,C,a,B,c$ alternativamente da due pencil con centri $G,H$, le linee

$X:=(A\cap b)(a\cap B),$

$Y:=(c\cap A)(C\cap a),$

$Z:=(b\cap C)(B\cap c)$

sono concorrenti, cioè: hanno un punto $U$ in comune.
Il diagramma a sinistra visualizza la versione proiettiva, quello a destra la versione affine, dove i punti $G,H$ sono punti all'infinito. Se il punto $U$ sta sulla retta $GH$ si ottiene il teorema di Pappo in "piccolo duale".

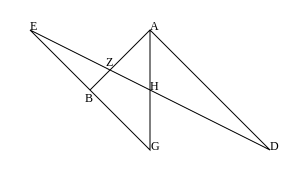
Se nella versione affine del teorema in "piccolo duale" il punto $U$ è anche un punto all'infinito, otteniamo il Teorema di Thomsen, un'affermazione su 6 punti sui lati di un triangolo (vedi diagramma). La figura di Thomsen gioca un ruolo essenziale nel coordinare una definizione un'assiomatica del piano proiettivo. La dimostrazione della chiusura della figura di Thomsen è quella del piccolo teorema, data sopra. Ma ne esiste anche una semplice diretta:

Visto che il teorema di Thomsen (la chiusura della figura) usa termini connesso, intersecato e parallelo, indica un'invarianza affine, e quindi possiamo introdurre le coordinate dei punti $P=(0,0),\;Q=(1,0),\;R=(0,1)$ (vedi diagramma destra). Il punto di partenza della sequenza di accordi è $(0,\lambda )$. Si verifica facilmente dalle coordinate dei punti dati nel diagramma, che l'ultimo punto coincide con il primo punto.

• 
  Costruzione di Thomsen (punti $\color {red}1,2,3,4,5,6$ del triangolo $PQR$) teorema di Pappo in piccolo duale ($U$ sempre punto all'infinito).
• 
  Dimostrazione di Thomsen

Enunciati equivalenti del teorema

I triangoli $XcC$ e $BbY$ sono prospettici da $A$ e $a$, ed anche da $Z$.

Oltre gli enunciati del teorema di Pappo e del suo duale, abbiamo le seguenti equivalenti affermazioni:

• Se i sei vertici di un esagono giacciono alternativamente su due rette, allora i tre punti di intersezione di coppie di lati opposti sono collineari.
• Se creiamo una matrice dei nove punti (confronta con la figura accanto) e pensiamo alla valutazione della quantità $\operatorname {perm} (M)$ di tale matrice, otteniamo come risultato che se le prime due righe e le sei triadi "diagonali" sono collineari, allora anche la terza riga è collineare.

M = $\left|{\begin{matrix}A&B&C\\a&b&c\\X&Y&Z\end{matrix}}\right|$

That is, if $\ ABC,abc,AbZ,BcX,CaY,XbC,YcA,ZaB\$ are lines, then Pappus's theorem states that $XYZ$ must be a line. Also, note that the same matrix formulation applies to the dual form of the theorem when $(A,B,C)$ etc. are triples of concurrent lines.

• Given three distinct points on each of two distinct lines, pair each point on one of the lines with one from the other line, then the joins of points not paired will meet in (opposite) pairs at points along a line.
• If two triangles are perspective in at least two different ways, then they are perspective in three ways.
• If $\;AB,CD,\;$ and $EF$ are concurrent and $DE,FA,$ and $BC$ are concurrent, then $AD,BE,$ and $CF$ are concurrent.

Origins

In its earliest known form, Pappus's Theorem is Propositions 138, 139, 141, and 143 of Book VII of Pappus's Collection. These are Lemmas XII, XIII, XV, and XVII in the part of Book VII consisting of lemmas to the first of the three books of Euclid's Porisms.

The lemmas are proved in terms of what today is known as the cross ratio of four collinear points. Three earlier lemmas are used. The first of these, Lemma III, has the diagram below (which uses Pappus's lettering, with G for Γ, D for Δ, J for Θ, and L for Λ).

Here three concurrent straight lines, AB, AG, and AD, are crossed by two lines, JB and JE, which concur at J. Also KL is drawn parallel to AZ. Then

KJ : JL :: (KJ : AG & AG : JL) :: (JD : GD & BG : JB).

These proportions might be written today as equations:

KJ/JL = (KJ/AG)(AG/JL) = (JD/GD)(BG/JB).

The last compound ratio (namely JD : GD & BG : JB) is what is known today as the cross ratio of the collinear points J, G, D, and B in that order; it is denoted today by (J, G; D, B). So we have shown that this is independent of the choice of the particular straight line JD that crosses the three straight lines that concur at A. In particular

(J, G; D, B) = (J, Z; H, E).

It does not matter on which side of A the straight line JE falls. In particular, the situation may be as in the next diagram, which is the diagram for Lemma X.

Just as before, we have (J, G; D, B) = (J, Z; H, E). Pappus does not explicitly prove this; but Lemma X is a converse, namely that if these two cross ratios are the same, and the straight lines BE and DH cross at A, then the points G, A, and Z must be collinear.

What we showed originally can be written as (J, ∞; K, L) = (J, G; D, B), with ∞ taking the place of the (nonexistent) intersection of JK and AG. Pappus shows this, in effect, in Lemma XI, whose diagram, however, has different lettering:

What Pappus shows is DE.ZH : EZ.HD :: GB : BE, which we may write as

(D, Z; E, H) = (∞, B; E, G).

The diagram for Lemma XII is:

The diagram for Lemma XIII is the same, but BA and DG, extended, meet at N. In any case, considering straight lines through G as cut by the three straight lines through A, (and accepting that equations of cross ratios remain valid after permutation of the entries,) we have by Lemma III or XI

(G, J; E, H) = (G, D; ∞ Z).

Considering straight lines through D as cut by the three straight lines through B, we have

(L, D; E, K) = (G, D; ∞ Z).

Thus (E, H; J, G) = (E, K; D, L), so by Lemma X, the points H, M, and K are collinear. That is, the points of intersection of the pairs of opposite sides of the hexagon ADEGBZ are collinear.

Lemmas XV and XVII are that, if the point M is determined as the intersection of HK and BG, then the points A, M, and D are collinear. That is, the points of intersection of the pairs of opposite sides of the hexagon BEKHZG are collinear.

Spazi R², A², P²

$\mathbb {R} ^{2}$, $\mathbb {A} ^{2}$, $\mathbb {P} ^{2}$

(1) Esagono reale in $\mathbb {R} ^{2}$. (2) Esagono di $\mathbb {A} ^{2}$. (3) Esagono di $\mathbb {P} ^{2}$

Il piano affine reale generalizza alcune proprietà degli spazi euclidei in modo tale che questi siano indipendenti dai concetti di distanza e misura degli angoli, mantenendo solo le proprietà relative al parallelismo e al rapporto delle lunghezze per i segmenti paralleli.

Il piano proiettivo reale è lo spazio di linee in R³ passante per l'origine. È una varietà differenziabile non orientabile 2-dimensionale, vale a dire una superficie che non può essere immersa senza auto-intersecarsi. Essa ha caratteristica di Eulero pari a 1 e quindi genere unitario.

Di conseguenza la figura dell'esagono subisce un cambio di forma nel passaggio tra i vari spazi: reale, affine, proiettivo. Questo si nota nella figura a destra.

Note

Postille

Bibliografia

• (EN) Pambuccian V., Schacht C., The axiomatic destiny of the theorems of Pappus and Desargues, in III.Geometry in history, Springer, 2019, pp. 355-399, DOI:10.1007/978-3-030-13609-3_8, ISBN 978-3-030-13611-6.