Teorema di Eulero (geometria)
In geometria euclidea, il nome di teorema di Eulero identifica almeno tre teoremi diversi.
Un teorema[modifica | modifica wikitesto]
Enunciato[modifica | modifica wikitesto]
In ogni triangolo l'ortocentro, il baricentro ed il circocentro sono allineati su una retta, detta retta di Eulero, e la distanza tra i primi due punti è doppia della distanza tra il baricentro ed il circocentro.[1]
Un altro teorema[modifica | modifica wikitesto]

Enunciato[modifica | modifica wikitesto]
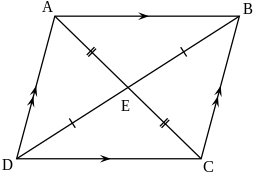
Sia un quadrilatero qualunque, e siano ed i punti medi delle diagonali e . Allora:
In altre parole, la somma dei quadrati delle lunghezze dei lati di un quadrilatero è pari alla somma dei quadrati delle lunghezze delle due diagonali del quadrilatero più 4 volte il quadrato della distanza tra i due punti medi delle diagonali.
Corollari[modifica | modifica wikitesto]
È interessante notare come questo teorema possa essere considerato una generalizzazione del Teorema di Pitagora. Si può infatti giungere ad una formula che metta in relazione i lati di un triangolo qualunque e la sua mediana. Per dimostrarlo consideriamo un Parallelogramma, che come tale ha le diagonali che si bisecano scambievolmente e i lati opposti uguali e quindi i due punti medi delle diagonali, coincidenti. Di conseguenza applicando il teorema di Eulero abbiamo che:
Quindi considerando il triangolo con mediana abbiamo che:
Quindi in ogni triangolo la somma dei quadrati costruiti su i due lati minori è uguale al doppio della somma dei quadrati costruiti sulla mediana e metà del terzo lato. Appunto considerando il caso del triangolo rettangolo si ha che la mediana è anche uguale a metà del terzo lato. La formula diventa quindi:
che è appunto il Teorema di Pitagora.
Un terzo teorema[modifica | modifica wikitesto]
Il nome teorema di Eulero può riferirsi anche al Teorema dei seni.
Note[modifica | modifica wikitesto]
- ^ Settimio Cirillo, Nuova geometria operativa, vol. 1, edizioni Ferraro, p. 143.