Tensione di snervamento
La tensione di snervamento o punto di snervamento di un materiale duttile è definita in scienza dei materiali come il valore della tensione in corrispondenza della quale il materiale inizia a deformarsi plasticamente, passando da un comportamento elastico reversibile ad un comportamento plastico caratterizzato dallo sviluppo di deformazioni irreversibili che non rientrano al venir meno della causa sollecitante. Nel caso di stati di tensione pluriassiale, il punto di snervamento indica la combinazione delle componenti di tensione che determina nel materiale la condizione di snervamento: gli infiniti punti di snervamento descrivono, nello spazio delle tensioni , una superficie detta superficie di snervamento.
La conoscenza del punto di snervamento di un materiale è di fondamentale importanza nel progetto di un componente o di un manufatto, in quanto esso generalmente segna il valore limite del carico a cui il componente o il manufatto può resistere. Tale conoscenza è anche importante per il controllo di molte tecniche di produzione materiali come forgiatura, laminazione e stampaggio.
Definizioni[modifica | modifica wikitesto]
È spesso difficoltoso definire precisamente lo snervamento a causa della vasta varietà di comportamenti esibiti dai materiali reali. Inoltre sono possibili diverse definizioni di snervamento. La definizione convenzionale tuttavia più largamente usata fa riferimento alla seguente definizione:
- Tensione di snervamento
- È il valore della tensione associato ad una deformazione plastica irreversibile del 0,2%, ricavata dalla curva tensione-deformazione relativa ad una prova di trazione su un provino di materiale di forma normata. La tensione di snervamento è usualmente indicata col simbolo o col simbolo (il pedice deriva dall'inglese yield strength).
Si hanno inoltre le seguenti definizioni:
- Vero limite elastico
- Il più basso valore della tensione rispetto alla quale le dislocazioni si attivano. Questa definizione è raramente utilizzata sia perché le dislocazioni si attivano a valori molto bassi di tensione, sia perché risulta molto difficile la sua rilevazione sperimentale.
- Limite di proporzionalità
- Il punto in corrispondenza del quale la curva tensione-deformazione devia dall'andamento lineare della legge di Hooke e diventa non lineare.
- Limite elastico
- Il più basso valore della tensione in corrispondenza del quale le deformazioni permanenti possono essere misurate. Tale misura richiede una procedura di carico e scarico e la sua accuratezza dipende molto dagli strumenti di misura e dalla capacità dell'operatore. Per gli elastomeri, come le gomme, il limite elastico è molto maggiore del limite di proporzionalità.
- Punto di snervamento superiore e punto di snervamento inferiore
- Alcuni metalli duttili, come l'acciaio al carbonio, presentano due punti di snervamento. Il loro comportamento è sostanzialmente lineare fino al raggiungimento del punto di snervamento superiore. Successivamente evidenziano un rapido salto ad un valore inferiore di tensione, il punto di snervamento inferiore che in ingegneria strutturale è assunto come valore conservativo di riferimento.
- Back stress
- Rappresenta il centro della curva limite di snervamento, che nel caso di materiali di Von Mises, è rappresentata da un'ellisse sul piano di Heigh Westergard. Il back stress è definito tramite un tensore.

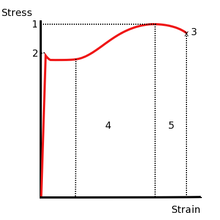
1: Vero limite elastico
2: Limite di proporzionalità
3: Limite elastico
4: Punto di snervamento
La superficie di snervamento[modifica | modifica wikitesto]
Nei modelli matematici della plasticità, la superficie di snervamento ha la seguente rappresentazione
in termini di una funzione di snervamento dipendente dalle generiche componenti dello stato tensionale in corrispondenza della condizione di snervamento.
Essendo il fenomeno dello snervamento rappresentativo, a livello macroscopico, di fenomeni che trovano spiegazione a livello microscopico, sulla scala del cristallino del materiale, la razionale costruzione della funzione di snervamento dovrebbe procedere a partire dai risultati della fisica dello stato solido. Per esempio nei metalli, tramite lo studio delle modalità di propagazione delle dislocazioni nel reticolo cristallino e del comportamento dei singoli grani, si dovrebbe caratterizzare il comportamento macroscopico degli aggregati cristallini di cui i metalli sono costituiti, giungendo quindi ad un migliore comprensione del comportamento plastico di questi. Questo programma è però lontano dall'essere completato: cioè allo stadio attuale delle ricerche non sono ancora disponibili teorie complete e consolidate che portino ad una costruzione razionale della funzione di snervamento.
Mancando una tale teoria microscopica, la superficie di snervamento può pertanto essere costruita solo per via empirica, assegnando empiricamente la funzione di snervamento con l'unica condizione che i risultati da essa previsti siano in buon accordo con i dati sperimentali. Su tale approccio si basa la strategia dei Criteri di resistenza, ed in particolare dei criteri di resistenza per materiali duttili.
Fattori che influenzano la tensione di snervamento[modifica | modifica wikitesto]
Il valore della tensione di snervamento dipende sia dalla velocità di deformazione (strain rate) che, più significativamente, dalla temperatura alla quale la deformazione avviene. Alder e Philips nel 1954 trovarono che la correlazione tra tensione di snervamento e velocità di deformazione (a temperatura costante) era ben descritta da una legge della seguente forma
dove C è una costante ed m è il coefficiente di velocità di deformazione. Tale coefficiente di sensibilità aumenta con l'aumentare della temperatura, materiali per i quali il m raggiunge valori maggiori di ~0.5 tendono ad esibire fenomeni di superplasticità.
Successivamente ai lavori di Alder e Philips sono state proposte altre e più complesse equazioni che tengono in conto simultaneamente i due fattori di temperatura e velocità di deformazione:
In questa α ed A sono costanti mentre Z è un fattore di compensazione spesso descritto dal parametro di Zener-Hollomon:
dove QHW è l'energia di attivazione per deformazione termiche e T è la temperatura assoluta.
Bibliografia[modifica | modifica wikitesto]
- L. Vergani, Meccanica dei Materiali, McGraw-Hill, Milano, 2001, ISBN 88-386-0860-1
- R. Baldacci, G. Ceradini, E. Giangreco, Plasticità, CISIA, Milano, 1974.
- R. Hill, The Mathematical Theory of Plasticity, Oxford University Press, 1998, ISBN 0-198-50367-9.
- M. Jirasek, Z. Bazant, Inelastic Analysis of Structures, Wiley, 2001, ISBN 0-471-98716-6.
- G. Dieter, Mechanical Metallurgy, McGraw-Hill, 1986, ISBN 978-0070168930
- Boresi, A. P., Schmidt, R. J., and Sidebottom, O. M. (1993). Advanced Mechanics of Materials, 5th edition. John Wiley & Sons. ISBN 0-471-55157-0
- Engineer's Handbook, su engineershandbook.com. URL consultato il 3 dicembre 2007 (archiviato dall'url originale il 25 agosto 2007).
Voci correlate[modifica | modifica wikitesto]
| Controllo di autorità | GND (DE) 4154637-4 |
|---|






![{\displaystyle \sigma _{y}={\frac {1}{\alpha }}\sinh ^{-1}\left[{\frac {Z}{A}}\right]^{(1/n)}\,\!}](https://wikimedia.org/api/rest_v1/media/math/render/svg/7ed5da44c0b1b2701dfb0f48ccc7cbb64e4c1a43)
