Quadrica
In matematica, e in particolare in geometria, una quadrica (o superficie quadrica) è una (iper-)superficie di uno spazio n-dimensionale sui complessi o sui reali rappresentata da un'equazione polinomiale del secondo ordine nelle variabili spaziali (coordinate). Se le coordinate spaziali sono , allora la generale quadrica nello spazio (o ) è definita da un'equazione della forma
dove è una matrice (non nulla), un vettore e una costante.
Un punto qualsiasi di una superficie quadrica si definisce iperbolico, parabolico o ellittico a seconda che il piano tangente alla superficie in quel punto tagli la quadrica in due rette reali e distinte, coincidenti o immaginarie coniugate. I punti di una quadrica sono tutti dello stesso tipo, cioè o tutti iperbolici o tutti parabolici o tutti ellittici. Tale caratteristica dipende solo dal segno del determinante della quadrica (invariante nei sistemi di riferimento cartesiani ortogonali) e viene spesso posta in evidenza come aggettivo della quadrica (ad esempio, iperboloide iperbolico).
Attraverso traslazioni e rotazioni ogni quadrica può essere trasformata in una forma "normalizzata", sensibilmente più semplice di quella generale. Ad esempio, l'equazione normalizzata di molte quadriche nello spazio a tre dimensioni () è:
Nello spazio euclideo tridimensionale ogni quadrica può essere scritta in una delle seguenti 9 forme normalizzate:
| Quadriche non degeneri | |||
|---|---|---|---|
| Ellissoide | Ellissoide scaleno | 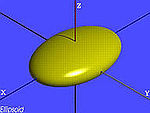
| |
| Sferoide prolato | |||
| Sferoide oblato | |||
| Sfera | |||
| Paraboloide | Paraboloide ellittico | 
| |
| Paraboloide circolare | |||
| Paraboloide iperbolico | 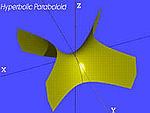
| ||
| Iperboloide | Iperboloide ad una falda (iperboloide iperbolico) | 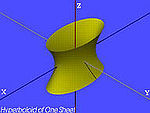
| |
| Iperboloide a due falde (iperboloide ellittico) | 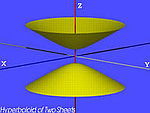
| ||
| Quadriche degeneri | |||
| Cono (a due falde) | 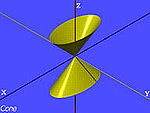
| ||
| Cilindro | Cilindro ellittico | 
| |
| Cilindro circolare | |||
| Cilindro parabolico | 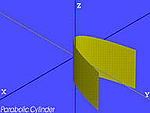
| ||
| Cilindro iperbolico | 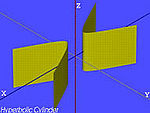
| ||
Nello spazio proiettivo reale, a meno di una trasformazione proiettiva ci sono tre classi di equivalenza di quadriche:
- il cono, il cilindro e le altre quadriche "degeneri", cioè con curvatura gaussiana zero, sono tra loro equivalenti;
- i due paraboloidi iperbolici e le superfici rigate sono tra loro equivalenti;
- l'ellissoide, il paraboloide ellittico, l'iperboloide a due falde e le rimanenti quadriche sono tra loro equivalenti.
Nello spazio proiettivo complesso tutte le quadriche non degeneri sono tra loro equivalenti, a meno di trasformazioni proiettive.
Bibliografia[modifica | modifica wikitesto]
- Giuseppe Vaccaro, Lezioni di geometria, vol. I, Roma, Veschi, 1975.
- Edoardo Sernesi, Geometria 2, Torino, Bollati Boringhieri, 1994, ISBN 978-88-339-5548-3.
Altri progetti[modifica | modifica wikitesto]
 Wikizionario contiene il lemma di dizionario «quadrica»
Wikizionario contiene il lemma di dizionario «quadrica»
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) quadric surface, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN) Eric W. Weisstein, Quadrica, su MathWorld, Wolfram Research.
- http://www.geom.uiuc.edu/docs/reference/CRC-formulas/node61.html, 16 Quadrics in Geometry Formulas and Facts di Silvio Levy, estratto dalla trentesima edizione di CRC Standard Mathematical Tables and Formulas (CRC Press).
| Controllo di autorità | Thesaurus BNCF 25756 · LCCN (EN) sh85109415 · BNF (FR) cb11981286v (data) · J9U (EN, HE) 987007550891005171 |
|---|






















