Moto di puro rotolamento
In fisica classica il moto di puro rotolamento è quello in cui un corpo rigido rotola senza strisciare. La rotazione avviene attorno al punto di contatto istantaneo che ha velocità nulla. La ruota che ha avuto una importanza fondamentale nello sviluppo della società moderna in condizioni normali di lavoro è ben descritta da questo tipo di moto. Normalmente la forza di attrito statico è quella che garantisce l'immobilità del punto di contatto, notiamo che dopo un tempo infinitesimo il punto di contatto diventa un punto infinitesimo vicino e via di seguito.
La forza di attrito statico non compie alcun lavoro, ma pur tuttavia, a causa della deformazione del punto di contatto, si ha una dissipazione di energia: tale effetto viene quantificato dall'attrito volvente. In ogni caso, questa forma di dissipazione dell'energia è in genere molto minore a quello che ci sarebbe se il punto di contatto strisciasse. Di conseguenza, per mantenere il moto di puro rotolamento viene richiesta un'energia molto minore rispetto a quella necessaria per fare strisciare gli oggetti.

Per avere moto di puro rotolamento è opportuno che l'oggetto sia simmetrico assialmente, anche se non è necessario. La sezione del corpo rigido è in genere un cerchio, tipicamente si ha a che fare quindi con cilindri o sfere.
Un punto qualsiasi sulla superficie durante il moto di puro rotolamento ha come traiettoria una cicloide.
Applicazioni[modifica | modifica wikitesto]
La maggior parte dei mezzi di trasporto moderni usano le ruote e quindi sfruttano il moto di puro rotolamento per lo spostamento. Lo slittamento deve essere evitato, altrimenti si perde il controllo del mezzo con gravi conseguenze pratiche. Accade di scivolare se la strada è coperta da neve, sabbia o olio o quando viene eseguita una curva a grande velocità o viene fatta una frenata brusca o una improvvisa accelerazione: cioè quando la forza di attrito statico non riesce ad ancorare il punto di contatto al suolo.
Una delle applicazioni principali del moto di rotolamento è l'uso dei cuscinetti a sfera. Normalmente sono delle sfere di metallo incapsulate tra due anelli che possono ruotare in maniera indipendente tra di loro. In molti meccanismi, l'anello interno è solidale con l'asse fisso. Quindi l'anello interno è fisso e quello esterno è libero di muoversi con poco attrito. Quasi tutti i motori (come quelli dei ventilatori, trapani o utensili elettrici in genere) hanno dei cuscinetti a sfera. L'attrito dipende dalla qualità dei cuscinetti a sfera e dalla loro lubrificazione.
Nelle società primitive per trasportare oggetti pesanti si usavano delle piattaforme piatte poggiate su cilindri di legno che permettevano con il riposizionamento continuo dei tronchi sulla parte frontale, in questa era possibile fare trasporti lineari su grandi distanze. Ovviamente nella società moderna si usano sistemi più semplici ed efficienti.
Dinamica[modifica | modifica wikitesto]
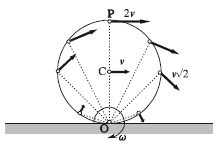
Indichiamo con il vettore che ha origine nel centro di massa del corpo rigido C e l'altro estremo sul punto istantaneo di contatto O con il piano di appoggio. La velocità angolare è un vettore normale al piano contenente la sezione del cerchio, con origine nel centro di massa. Nel moto dei corpi rigidi è sempre possibile descrivere il moto di un qualsiasi punto come la combinazione del moto traslatorio del centro di massa e la rotazione attorno ad un asse passante per il centro di massa. In particolare quindi la velocità del punto di contatto è descritta dalla relazione:
Imponendo che tale velocità sia nulla si ha che:
Quindi se il corpo si muove verso destra, come nella figura, la rotazione avviene in senso orario. In modulo quindi
cioè nel moto di puro rotolamento esiste una relazione ben precisa tra la velocità del centro di massa e la velocità angolare (che non dipende dalla scelta del polo). Se quindi la velocità del centro di massa cambia nel tempo, cioè il moto è accelerato, la stessa cosa deve fare la velocità angolare per cui anche:
avendo indicato con la accelerazione del centro di massa e con la accelerazione angolare.
Energia[modifica | modifica wikitesto]
Detta la velocità angolare istantanea il moto nel punto di contatto è un moto solo rotatorio e se il momento di inerzia del corpo attorno al punto di contatto è l'energia cinetica è rotazionale vale:
Se il corpo rigido è simmetrico assialmente, con massa e distanza tra il punto di contatto e il centro di massa pari a , per il teorema di Huygens-Steiner la relazione che lega e il momento di inerzia parallelo passante per il centro di massa è:
Quindi posso anche scrivere:
Ma nel moto di puro rotolamento si ha che , quindi
Cioè il moto di puro rotolamento è la combinazione di un moto rotatorio e traslatorio del centro di massa con una energia cinetica rotazionale ed una traslazionale .
Alcuni casi particolari[modifica | modifica wikitesto]
Moto di puro rotolamento con sola forza applicata al centro di massa[modifica | modifica wikitesto]

Immaginiamo di avere un corpo rigido a sezione circolare di raggio e massa come mostrato in figura su cui agisce una forza motrice sul centro di massa parallela al piano di appoggio orizzontale (questo è il caso delle ruote non motrici di una automobile). La figura mette in evidenza le varie forze agenti sul corpo: la parallela al piano applicata sul centro di massa; la forza di attrito statico; la forza peso , la reazione vincolare . La reazione vincolare bilancia esattamente la forza peso (se la superficie fosse un piano inclinato l'equazioni sarebbero diverse):
Mentre per quanto riguarda la direzione orizzontale, l'equazione oraria (prima equazione cardinale) è:
Per quanto riguarda il momento angolare (seconda equazione cardinale), definendo con il momento di inerzia rispetto all'asse di rotazione del corpo e scelto il centro di massa come polo:
Eguagliando le due espressioni cioè imponendo che il moto sia di puro rotolamento:
L'unica incognita diventa la forza di attrito che vale:
Quindi la forza di attrito in modulo è sempre inferiore al valore della forza trainante. Ma in ogni caso deve anche valere la condizione che:
Questo impone che per garantire un moto di puro rotolamento la forza da applicare al centro di massa deve essere inferiore ad un certo valore massimo:
Notare che se venisse applicata una forza maggiore di , il punto di contatto striscerebbe, in quanto la forza di attrito statico non sarebbe più sufficiente a bloccarlo sul piano di appoggio, si avrebbe quindi che il moto non sarebbe di puro rotolamento in quanto:
Via via che crescesse la forza applicata il moto traslatorio prevarrebbe sul moto rotatorio.
La funzione dell'attrito statico è essenziale nel moto di puro rotolamento, in quanto causa un momento di una forza (fR) che fa ruotare il corpo, e quindi il corpo trasla (per effetto della forza F applicata) e contemporaneamente ruota a causa dell'attrito. Se non ci fosse attrito il corpo semplicemente traslerebbe. Notare che se la sezione del corpo ruotante non fosse perfettamente circolare il moto diventerebbe in quei punti di contatto prevalentemente traslatorio e la forza di attrito svolgerebbe anche un'azione frenante; l'esempio più chiaro è il caso delle ruote delle automobili non motrici sgonfie.
Se la forza fosse stata frenante, quindi con direzione opposta alla direzione del moto, anche la forza di attrito avrebbe avuto direzione opposta, matematicamente tutte le equazioni sarebbero rimaste eguali, sarebbe la forza frenante massima applicabile.
Moto di puro rotolamento con solo momento applicato sull'asse[modifica | modifica wikitesto]

Immaginamo di avere una ruota sul cui asse è applicato un momento motore . Questo è il caso delle ruote motrici di una automobile. Nella figura sono mostrate le forze ed il momento. Immaginiamo che il moto si svolga su un piano orizzontale. Notare che il verso della forza di attrito è opposto al caso precedente.
La reazione vincolare bilancia esattamente la forza peso come nel caso precedente. Ma per quanto riguarda la componente orizzontale si ha:
Per quanto riguarda il momento angolare, tenendo presente che se il momento fa ruotare il corpo in senso orario, la forza di attrito esercita un momento in direzione opposta:
Eguagliando le due espressioni (condizione necessaria per avere moto di puro rotolamento):
Da cui si ricava che vale:
la forza d'attrito è la forza motrice che causa il moto traslatorio, ma anche in questo caso si ha la condizione che:
e quindi:
Se il momento applicato è maggiore di il moto rotatorio è prevalente sul moto traslatorio. Questo è il caso delle ruote motrici di una automobile quando su di esse viene applicato un momento maggiore di quello che permette la trazione e le ruote slittano. La forza di attrito è la forza che causa il moto traslatorio, la ragione per cui gli pneumatici delle automobili sono fatti di gomma è per avere un elevato attrito statico con il fondo stradale.
Notiamo che se ci fosse stato un momento frenante la forza di attrito avrebbe avuto verso opposto, ed avrebbe quindi l'effetto di rallentare il moto. Ma l'espressione del momento massimo applicabile sarebbe stata la stessa.
Moto di puro rotolamento con un momento ed una forza applicata[modifica | modifica wikitesto]

Immaginiamo che il moto si svolga su un piano inclinato in salita con inclinazione , sul corpo agisce un momento motore . La forza peso ha una componente tangenziale al piano e una normale . La reazione vincolare bilancia esattamente la componente della forza peso perpendicolare al piano:
Mentre la legge del moto nella direzione del piano di appoggio è:
Per quanto riguarda il momento angolare tenendo presente che, se il momento fa ruotare il corpo in senso orario, la forza di attrito esercita un momento in direzione opposta:
Dalla condizione che il moto sia di puro rotolamento segue che:
Imponendo la condizione che:
Si ha che per avere moto di puro rotolamento:
Vi è anche una inclinazione massima del piano inclinato al di sopra della quale qualsiasi moto di puro rotolamento non è possibile (quando è nullo ) cioè se si ha che .
In discesa è possibile un moto di puro rotolamento anche in assenza di attrito per un opportuno momento motore. Se in discesa la forza di attrito cambia segno rispetto a quanto indicato nella figura.
Palla da biliardo[modifica | modifica wikitesto]
Immaginiamo di avere una palla da biliardo di massa , raggio , momento di inerzia rispetto al centro colpita da un impulso parallelo al piano d'appoggio esattamente all'altezza centrale. La variazione di quantità di moto della palla è pari all'impulso ricevuto:
Mentre la velocità angolare iniziale è nulla. Se il coefficiente di attrito dinamico è pari . Utilizzando la prima equazione cardinale:
Quindi inizialmente il moto è moto rettilineo uniformemente accelerato la cui equazione oraria è:
La forza di attrito essendo applicata sul punto di contatto esercita un momento e quindi usando la seconda equazione cardinale:
Per cui inizialmente la velocità angolare aumenta linearmente:
Quando si verifica che:
cioè quando:
Il moto diviene di puro rotolamento e la velocità del centro di massa e la velocità angolare non variano più. In realtà esiste l'attrito volvente che è stato trascurato nel ragionamento che esercita una debole azione frenante.
Bibliografia[modifica | modifica wikitesto]
- P. Mazzoldi, N. Nigro e C. Voci, FIsica Volume 1, 2ª ed., Napoli, EdiSes Wiley, 2003, ISBN 88-7959-137-1.
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file su moto di puro rotolamento
Wikimedia Commons contiene immagini o altri file su moto di puro rotolamento



















































![{\displaystyle \theta \geq arctg\left[\mu _{s}\left(MR^{2}/I+1\right)\right]\ }](https://wikimedia.org/api/rest_v1/media/math/render/svg/a0aa3da7af1aa376b6f913a8c0c90f5379b9f9d5)











