Grafo di Turán
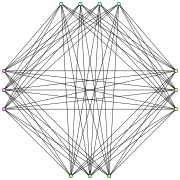
Il grafo di Turán T(n,r) è un grafo formato suddividendo un insieme di n vertici in r sottoinsiemi, con dimensioni più uguali possibili, e connettendo due vertici mediante uno spigolo ogni volta che appartengono a sottoinsiemi diversi. Il grafo avrà sottoinsiemi di dimensione , e sottoinsiemi di dimensione . Ossia, è un grafo r-partito completo
Ciascun vertice ha grado o o . Il numero di spigoli è
È un grafo regolare, se n è divisibile per r.
Teorema di Turán[modifica | modifica wikitesto]
I grafi di Turán prendono il nome da Pál Turán, che li usò per dimostrare il teorema di Turán, un importante risultato nella teoria dei grafi estremali.
Per il principio dei cassetti, ogni insieme di r + 1 vertici nel grafo di Turán include due vertici nello stesso sottoinsieme di partizione; perciò, il grafo di Turán non contiene una cricca di dimensione r + 1. Secondo il teorema di Turán, il grafo di Turán ha il massimo numero possibile di spigoli tra tutti i grafi senza (r + 1)-cricche con n vertici. Keevash e Sudakov (2003) mostrano che il grafo di Turán è anche l'unico grafo senza (r + 1)-cricche di ordine n nel quale ogni sottoinsieme di αn vertici abbraccia almeno spigoli, se α è sufficientemente vicino a 1. Il teorema di Erdős–Stone estende il teorema di Turán limitando il numero di spigoli di un grafo che non ha un grafo fisso di Turán come sottografo. Attraverso questo teorema, limiti simili nella teoria dei grafi estremali possono essere dimostrati per qualsiasi sottografo escluso, a seconda del numero cromatico del sottografo.
Casi speciali[modifica | modifica wikitesto]

Varie scelte del parametro r in un grafo di Turán conducono a grafi particolari che sono stati studiati indipendentemente.
Il grafo di Turán T(2n,n) può essere formato rimuovendo un accoppiamento perfetto da un grafo completo K2n. Come mostrò Roberts (1969), questo grafo ha bossicità esattamente n; esso è noto a volte come grafo di Roberts. Questo grafo è anche l'1-scheletro di un politopo incrociato n-dimensionale; ad esempio, il grafo T(6,3) = K2,2,2 è il grafo ottaedrico, il grafo dell'ottaedro regolare. Se n coppie vanno a una festa, e ciascuna persona stringe la mano a ogni persona eccetto il suo compagno o la sua compagna, allora questo grafo descrive l'insieme delle strette di mano che hanno luogo; per questa ragione esso è chiamato anche il grafo del cocktail party.
Il grafo di Turán T(n,2) è un grafo bipartito completo e, quando n è pari, un grafo di Moore. Quando r è un divisore di n, il grafo di Turán è simmetrico e fortemente regolare, sebbene alcuni autori considerino i grafi Turán come un caso banale di forte regolarità e perciò li escludano dalla definizione di un grafo fortemente regolare.
Il grafo di Turán ha 3a2b cricche massimali, dove 3a + 2b = n and b ≤ 2; ciascuna cricca massimale è formata scegliendo un vertice da ciascun sottoinsieme di partizione. Questo è il più grande numero di cricche massimali possibili fra tutti i grafi con n vertici indipendentemente dagli spigoli nel grafo (Moon e Moser (1965)); questi grafi sono chiamati talvolta grafi di Moon-Moser.
Altre proprietà[modifica | modifica wikitesto]
Ogni grafo di Turán è un cografo; cioè, può essere formato a partire dai singoli vertici mediante una sequenza di operazioni di unione disgiunta e di complemento. Specificamente, tale sequenza può cominciare formando ciascuno degli insiemi indipendenti del grafo di Turán come un'unione disgiunta di vertici isolati. Poi, il grafo complessivo è il complemento dell'unione disgiunta dei complementi di questi insiemi indipendenti.
Chao e Novacky (1982) mostrano che i grafi di Turán sono cromaticamente unici: nessun altro grafo ha gli stessi polinomi cromatici. Nikiforov (2005) usa i grafi di Turán per fornire un limite inferiore per la somma dei k-esimi autovalori di un grafo e del suo complemento.
Falls, Powell e Snoeyink sviluppano un algoritmo efficiente per raggruppamenti di gruppi di geni ortologhi nei dati genomici, rappresentando i dati come un grafo e cercando grandi sottografi di Turán.
I grafi di Turán hanno anche alcune interessanti proprietà legate alla teoria geometrica dei grafi. Pór e Wood (2005) danno un limite inferiore di Ω((rn)3/4) sul volume di qualsiasi incorporazione a griglia tridimensionale del grafo di Turán. Witsenhausen (1974) congettura che la somma massima delle distanze al quadrato, tra n punti con diametro unitario in Rd, si raggiunge per una configurazione formata incorporando un grafo di Turán sui vertici di un simplesso regolare.
Un grafo G con n vertici è un sottografo di un grafo di Turán T(n,r) se e solo se G ammette una colorazione equa con r colori. La partizione del grafo di Turán in insiemi indipendenti corrisponde alla partizione di G in classi di colore. In particolare, il grafo di Turán è l'unico grafo massimale su n vertici con una colorazione equa di r colori.
Bibliografia[modifica | modifica wikitesto]
- Chao, C. Y.; Novacky, G. A., On maximally saturated graphs, in Discrete Mathematics, vol. 41, n. 2, 1982, pp. 139–143, DOI:10.1016/0012-365X(82)90200-X.
- Falls, Craig; Powell, Bradford; Snoeyink, Jack, Computing high-stringency COGs using Turán type graphs (PDF).
- Keevash, Peter; Sudakov, Benny, Local density in graphs with forbidden subgraphs, in Combinatorics, Probability and Computing, vol. 12, n. 2, 2003, pp. 139–153, DOI:10.1017/S0963548302005539.
- Moon, J. W. e Moser, L., On cliques in graphs, in Israel Journal of Mathematics, vol. 3, 1965, pp. 23–28, DOI:10.1007/BF02760024.
- Nikiforov, Vladimir, Eigenvalue problems of Nordhaus-Gaddum type, 2005, arXiv:math.CO/0506260.
- Pór, Attila; Wood, David R., Proc. Int. Symp. Graph Drawing (GD 2004), No-three-in-line-in-3D, Lecture Notes in Computer Science no. 3383, Springer-Verlag, 2005, pp. 395–402, DOI:10.1007/b105810.
- Roberts, F. S., On the boxicity and cubicity of a graph, in Recent Progress in Combinatorics, Academic Press, 1969, pp. 301–310.
- Turán, P., On an extremal problem in graph theory, in Matematiko Fizicki Lapok, vol. 48, 1941, pp. 436–452.
- Witsenhausen, H. S., On the maximum of the sum of squared distances under a diameter constraint, in American Mathematical Monthly, vol. 81, n. 10, The American Mathematical Monthly, Vol. 81, No. 10, 1974, pp. 1100–1101, DOI:10.2307/2319046, JSTOR 2319046.
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file su grafo di Turán
Wikimedia Commons contiene immagini o altri file su grafo di Turán
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) Eric W. Weisstein, Grafo di Turán, su MathWorld, Wolfram Research.









