Grafo planare
Nella teoria dei grafi si definisce grafo planare un grafo che può essere raffigurato in un piano in modo che non si abbiano archi che si intersecano. Ad esempio sono planari i seguenti grafi:
Il secondo può essere raffigurato senza archi che si intersecano spostando uno degli archi dati da una diagonale al di fuori del perimetro del quadrato.
Vi sono invece grafi che posseggono solo raffigurazioni piane nelle quali si hanno coppie di archi che si intersecano. Le due seguenti figure forniscono raffigurazioni di due grafi non planari:
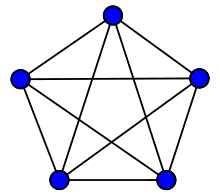

Si tratta del grafo completo con 5 nodi e del grafo bipartito completo con 3+3 nodi ; questi due grafi sono chiamati anche grafi di Kuratowski, in onore del matematico polacco Kazimierz Kuratowski. Si constata infatti che non è possibile ridisegnare queste raffigurazioni evitando che gli archi si intersechino. In effetti Kuratowski nel 1929 ha dimostrato che questi sono i due grafi non planari più ridotti, con il seguente enunciato.
Teorema di Kuratowski[modifica | modifica wikitesto]
Teorema di Kuratowski:
- Un grafo è planare se e solo se non contiene alcun sottografo che sia un'espansione di o un'espansione di .
Ricordiamo che per espansione di un grafo G si intende un grafo che si ottiene da G attraverso manovre di inserimento di nodi negli archi, cioè modificando uno spigolo * --- * nella coppia di archi adiacenti * --- * --- *; queste manovre possono essere effettuate nessuna, una o più volte.
Questo teorema è conosciuto anche come Teorema P e possiede diverse formulazioni equivalenti
- Un grafo è planare se e solo se non contiene alcun sottografo che sia omeomorfo a o a .
- Un grafo è planare se e solo se non contiene tra i suoi minori né né .
Una generalizzazione di ampia portata del teorema di Kuratowski è costituita dal teorema di Robertson-Seymour; questo enunciato considera e come "minori proibiti" per i grafi planari.
Algoritmi e criteri di planarità[modifica | modifica wikitesto]
Nella pratica, se occorre decidere rapidamente se un dato grafo è planare, non è facile servirsi del criterio che si individua nel teorema di Kuratowski. Esistono invece degli algoritmi che consentono di decidere rapidamente la planarità di molti grafi: per certi grafi con n nodi è possibile stabilire se sono planari o meno in un tempo O(n).
Per un grafo semplice, connesso e planare con n nodi ed e archi si dimostra:
- Teorema 1. Se n ≥ 3, allora e ≤ 3n - 6
- Teorema 2. Se n > 3 e non vi sono cicli di lunghezza 3, allora e ≤ 2n - 4
Si noti che questi enunciati riguardano condizioni necessarie, non condizioni sufficienti: quindi possono essere invocati per dimostrare che un grafo non è planare, ma non per dimostrare che sia planare. Vi sono casi nei quali i Teoremi 1 e 2 non si possono applicare: in tali circostanze si deve ricorrere al Teorema P.
Il grafo K3,3 ha 6 nodi, 9 archi e nessun ciclo di lunghezza 3. Quindi per il Teorema 2 è non planare.
I grafi planari sono grafi relativamente agevoli da trattare: in effetti dati due grafi planari di n nodi, è possibile stabilire se sono isomorfi o meno in tempi O(n).
Il criterio di planarità di MacLane fornisce una caratterizzazione algebrica dei grafi planari mediante i corrispondenti spazi dei cicli.
La formula di Eulero[modifica | modifica wikitesto]
La formula di Eulero afferma che se un grafo connesso planare è disegnato nel piano senza intersezioni del bordo, v è il numero di vertici, e è il numero di bordi ed f è il numero di facce (regioni limitate dai bordi, inclusa la regione esterna infinitamente grande), allora:
v − e + f = 2,
In altre parole, la caratteristica di Eulero è 2. Come nell'illustrazione, nel primo grafo planare mostrato su, abbiamo v=6, e=7 e f=3. Se il secondo grafo è ridisegnato senza archi che si intersecano, abbiamo ‘'v’'=4, ‘'e’'=6 e f= 4. La formula di Eulero può essere dimostrata come segue: se il grafo non è un albero, allora togliamo uno spigolo che completa un ciclo. Questo abbassa sia e che f di una unità, lasciando invariato v − e + f. Si può ripetere la manovra fino ad ottenere un albero. Gli alberi hanno v=e +1 e f=1, dimostrando che v - e + f = 2.
In un grafo planare finito, semplice e connesso, qualsiasi faccia (eccetto quella illimitata) è limitata da almeno tre archi e ogni spigolo è incidente di al più due facce; usando la formula di Eulero, si può dimostrare che questi grafi sono sparsi nel senso che e ≤ 3v - 6 if v ≥ 3.
Notiamo che la formula di Eulero è valida anche per i poliedri semplici. Questa non è una coincidenza: ogni poliedro semplice può essere trasformato in un grafo semplice connesso usando i vertici del poliedro come vertici del grafo e gli spigoli del poliedro come archi del grafo. Le facce del grafo planare risultante corrispondono alle facce del poliedro. Per esempio il secondo grafo planare mostrato all'inizio corrisponde al tetraedro. Non tutti i grafi planari connessi semplici possono essere associati a poliedri semplici; ad esempio gli alberi non possono essere riguardati come poliedri. Un teorema di Ernst Steinitz dice che i grafi planari associati ai poliedri convessi (o equivalentemente quelli associati a poliedri semplici) sono precisamente i grafi planari semplici 3-connessi.
Casi particolari[modifica | modifica wikitesto]
Grafi massimali[modifica | modifica wikitesto]
Un grafo semplice è chiamato planare massimale se è planare, e se con l'aggiunta di un qualunque nuovo spigolo tra due vertici presenti fa cadere la planarità. Tutte le facce (eccetto al più una) sono allora limitate da tre archi; questo giustifica il termine alternativo di grafo triangolare che si usa per questi grafi. Se un grafo triangolare ha v vertici con v>2, allora ha precisamente 3v-6 archi e 2v-4 facce.
Grafi planari esterni[modifica | modifica wikitesto]
Un grafo è chiamato planare esterno se è immerso in un piano in modo che i vertici giacciono su una circonferenza e gli archi si trovano all'interno del corrispondente cerchio e non si intersecano. In maniera equivalente, c'è una faccia che in una opportuna raffigurazione include ogni vertice. Ovviamente, ogni grafo planare esterno è un grafo planare, ma il viceversa non è vero: il secondo esempio mostra che K4 (il grafo completo su quattro vertici) è un grafo planare, ma non un grafo planare esterno. Esso è il più piccolo grafo planare non esterno: si ha un teorema simile a quello di Kuratowski che afferma che un grafo finito è planare esterno se e solo se non contiene un sottografo che è un'espansione di K4 o del grafo bipartito completo K2,3 (5 vertici, 2 dei quali connessi ad ognuno dei tre per un totale di sei archi).
Ulteriori proprietà[modifica | modifica wikitesto]
Ogni grafo planare senza cappi è tetrapartito, o 4-colorabile; questa è la formulazione in termini della teoria dei grafi del teorema dei quattro colori.
Tutti gli alberi finiti e gli alberi numerabili sono planari esterni e quindi planari.
Si dimostra che ogni grafo semplice planare ammette un'immersione nel piano tale che tutti gli archi sono segmenti rettilinei che non si intersecano. Si dimostra anche che ogni grafo semplice planare esterno ammette un'immersione nel piano tale che tutti i vertici giacciono su una circonferenza e tutti gli archi sono segmenti rettilinei che giacciono all'interno del corrispondente cerchio e non si intersecano.
Voci correlate[modifica | modifica wikitesto]
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file sul grafo planare
Wikimedia Commons contiene immagini o altri file sul grafo planare
Collegamenti esterni[modifica | modifica wikitesto]
- (EN) planar graph, su Enciclopedia Britannica, Encyclopædia Britannica, Inc.
- (EN) Eric W. Weisstein, Grafo planare, su MathWorld, Wolfram Research.



