Epigrafico (matematica)
Vai alla navigazione
Vai alla ricerca
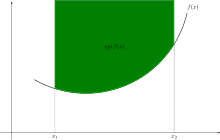
In analisi matematica, l'epigrafico di una funzione
definita su un insieme è l'insieme di punti che stanno al di sopra o sul grafico della funzione:
Se è un sottoinsieme di , l'epigrafico è un sottoinsieme di .
Proprietà[modifica | modifica wikitesto]
Convessità[modifica | modifica wikitesto]
Nell'ipotesi:
Una funzione è convessa se e solo se il suo epigrafico è un insieme convesso. Un insieme A è detto convesso se i segmenti che hanno estremi in A sono tutti suoi sottoinsiemi
Funzioni lineari[modifica | modifica wikitesto]
L'epigrafico di una funzione affine reale
è un semispazio di .
Semicontinuità[modifica | modifica wikitesto]
Una funzione è inferiormente semicontinua se e solo se il suo epigrafico è chiuso.






