Ceviana

In geometria, una ceviana è genericamente un segmento che congiunge un vertice del triangolo al suo lato opposto, o al suo prolungamento; mentre con retta ceviana si intende per estensione la retta su cui giace.

Particolarmente importanti sono le ceviane concorrenti in un unico punto, detto appunto ceviano – le cui condizioni di sufficienza sono dettate dal teorema di Ceva – designando sui lati opposti anche tre punti che sono i vertici del relativo triangolo ceviano il cui circumcerchio è detto cerchio ceviano.

Lunghezza

Un triangolo con una ceviana di lunghezza $d$

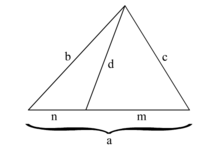
Teorema di Stewart

La lunghezza di una ceviana può essere calcolata con il teorema di Stewart. Nella figura, la lunghezza della ceviana $d$ è data dalla formula:

$b^{2}m+c^{2}n=a(d^{2}+mn).$

Mediana

La ceviana può essere una mediana. In questo caso la sua lunghezza è data dalla formula:

$m(b^{2}+c^{2})=a(d^{2}+m^{2})$

oppure

$2(b^{2}+c^{2})=4d^{2}+a^{2}$

da cui

$a=2m.$

In questo caso

$d={\sqrt {\frac {2b^{2}+2c^{2}-a^{2}}{4}}}.$

Bisettrice

La ceviana può essere una bisettrice. In questo caso la sua lunghezza è data dalla formula:

$(b+c)^{2}=a^{2}\left({\frac {d^{2}}{mn}}+1\right),$

e

$d^{2}+mn=bc$

e

$d={\frac {2{\sqrt {bcs(s-a)}}}{b+c}}$

dove $s=(a+b+c)/2$ è il semiperimetro.

Il lato di lunghezza $a$ è diviso secondo la proporzione $b:c$.

Altezza

La ceviana può essere una altezza del triangolo. In questo caso la sua lunghezza è data dalla formula:

$d^{2}=b^{2}-n^{2}=c^{2}-m^{2}$

e

$d={\frac {2{\sqrt {s(s-a)(s-b)(s-c)}}}{a}},$

dove $s=(a+b+c)/2$ è il semiperimetro.

Ceviane concorrenti

O è il punto ceviano e AA', BB' e CC' sono le ceviane

Tre ceviane concorrenti individuano un punto ceviano che può essere sia interno che esterno al perimetro del triangolo; nel primo caso anche tutte e tre le ceviane sono interne alla figura, invece quando è esterno solo una rimane interna e lo raggiunge solo se prolungata, mentre le altre due incrociano direttamente il punto e intersecano i prolungamenti dei lati.

O è il punto ceviano e AA', BB' e CC' sono le ceviane

È possibile determinare anche la lunghezza delle ceviane concorrenti avendo coordinate trilineari (α, β, γ) del punto di concorrenza, le lunghezze dei rispettivi lati a, b e c i lati del triangolo, attraverso la seguente formula:

$o_{i}={\frac {\sqrt {l_{j}l_{k}[l_{j}l_{k}(\omega _{j}^{2}+\omega _{k}^{2})+\omega _{j}\omega _{k}(l_{j}^{2}+l_{k}^{2}-l_{i}^{2})]}}{l_{j}\omega _{j}+l_{k}\omega _{k}}}$

dove l_x indica il lato e ω_x la coordinata trilineare relativa del punto.

Il punto di concorrenza inoltre segna sulle tre ceviane tre rapporti r_i tra la sua distanza dal vertice I e il punto di intersezione col lato opposto:

$r_{a}={\frac {AO}{OA'}}$; $r_{b}={\frac {BO}{OB'}}$; $r_{c}={\frac {CO}{OC'}}$

Per questi rapporti valgono le seguenti relazioni di somme e prodotto:

$r_{a}+r_{b}+r_{c}={\frac {b\beta +c\gamma }{a\alpha }}+{\frac {a\alpha +c\gamma }{b\beta }}+{\frac {a\alpha +b\beta }{c\gamma }}$

$r_{a}r_{b}r_{c}={\frac {(a\alpha +b\beta )(b\beta +c\gamma )(a\alpha +c\gamma )}{abc\alpha \beta \gamma }}$

i cui valori sono rispettivamente ≥6 e a ≥8.

Collegamenti esterni

• (EN) Eric W. Weisstein, Ceviana, su MathWorld, Wolfram Research.
• (EN) Ross Honsberger, Episodes in Nineteenth and Twentieth Century Euclidean Geometry, MAA, Cambridge University Press, 1995 ISBN 978-0-88385-639-0, p. 13 et 137.
• (EN) Vladimir Karapetoff, Some properties of correlative vertex lines in a plane triangle, American Mathematical Monthly, 36 (1929), 476–9 jstor.