Bipiramide quadrata elongata

Bipiramide quadrata elongata
Tipo	Solido di Johnson J14 - J15 - J16
Forma facce	8 Triangoli 4 Quadrati
Nº facce	12
Nº spigoli	20
Nº vertici	10
Caratteristica di Eulero	2
Incidenza dei vertici	2(34) 8(32.42)
Gruppo di simmetria	D4h, [4,2], (*422)
Gruppo rotazionale	D4, [4,2]+, (422)
Duale	Bitronco quadrato
Proprietà	Convessità
Politopi correlati
Poliedro duale
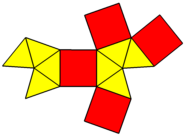
Sviluppo piano

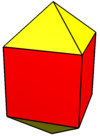
In geometria solida, la bipiramide quadrata elongata è un solido di 12 facce che può essere costruito, come intuibile dal suo nome, allungando una bipiramide quadrata, ossia un ottaedro, attraverso l'aggiunta di un prisma quadrangolare, ossia un parallelepipedo, tra le sue due metà congruenti.

Caratteristiche

Nel caso in cui tutte le sue facce siano poligoni regolari, la bipiramide quadrata elongata diventa uno dei 92 solidi di Johnson, in particolare quello indicato come J₁₅, ossia un poliedro strettamente convesso avente come facce dei poligoni regolari ma comunque non appartenente alla famiglia dei poliedri uniformi.

Formule

Considerando una bipiramide quadrata elongata avente come facce dei poligoni regolari aventi lato di lunghezza $a$, le formule per il calcolo del volume $V$, della superficie $A$ e dell'altezza $h$ risultano essere:

$V=\left(1+{\frac {\sqrt {2}}{3}}\right)a^{3}\approx 1,471404521\cdot a^{3};$

$A=\left(4+2{\sqrt {3}}\right)a^{2}\approx 7,464101615\cdot a^{2};$

$h=\left(1+{\sqrt {2}}\right)a\approx 2,414213562\cdot a.$

Poliedro duale

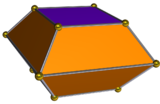
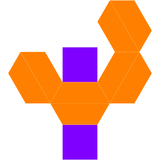
Il poliedro duale di una bipiramide quadrata elongata è un bitronco quadrato, il quale ha 10 facce: otto trapezoidali e due quadrate.

Poliedro duale	Sviluppo piano del duale

Poliedri e tassellature dello spazio correlati

Un tipo particolare di bipiramide quadrata elongata avente come facce triangolari dei triangoli isosceli con i lati in rapporto 2:${\sqrt {3}}$:${\sqrt {3}}$ permette di realizzare una tassellatura dello spazio euclideo, si tratta quindi di una tassellatura eseguita con un ottaedro oblato elongato, di cui si riporta qui sotto anche lo sviluppo piano.

Tale tassellatura può essere considerata come una fase di transizione la tassellatura cubica e quella rombododecaedrica. Come si vede nelle figure sottostanti, in cui le celle sono colorate di bianco, rosso e blu a seconda della loro orientazione spaziale, in questa tassellatura spaziale avente simmetria [[4,3,4]] le parti piramidali di sei diverse celle a forma di bipiramide quadrata elongata si incontrano a formare un cubo. Il duale di questa tassellatura, avente anch'esso simmetria [[4,3,4]], è composto da due tipi di ottaedri, ossia ottaedri regolari e antiprismi triangolari.

Sezionando la suddetta tassellatura lungo i centri delle celle si ottiene una tassellatura quadrata smussata, con esagoni schiacciati orientati verticalmente e orizzontalmente, e quadrati.

Tassellatura dello spazio

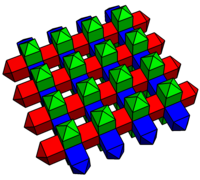Semi tassellatura dello spazio

Tassellatura quadrata smussata

Una bipiramide quadrata elongata con tutte le facce regolari può essere utilizzata per realizzare una tassellatura dello spazio assieme a tetraedri e ottaedri regolari; questi ultimi possono a loro volta essere scomposti in piramidi quadrate. La tassellatura risultante può essere considerata una versione allungata della tassellatura tetra-ottaedrica.

Collegamenti esterni

• (EN) Eric W. Weisstein, Bipiramide quadrata elongata, su MathWorld, Wolfram Research.