Bipiramide pentagonale

Bipiramide pentagonale
Tipo	Bipiramide; Solido di Johnson; J12 - J13 - J14
Forma facce	Triangoli
Nº facce	10
Nº spigoli	15
Nº vertici	7
Caratteristica di Eulero	2
Incidenza dei vertici	V4.4.5
Notazione di Schläfli	{ } + {5}
Diagramma di Coxeter-Dynkin
Gruppo di simmetria	D3h, [3,2], (*223) ordine 12
Gruppo rotazionale	D5, [5,2]+, (225), ordine 10
Duale	Prisma pentagonale
Proprietà	Convessità, transitivo per facce
Politopi correlati
	Poliedro duale
Sviluppo piano
	Manuale

In geometria solida, la bipiramide pentagonale è un decaedro che risulta essere anche il terzo elemento di un insieme infinito di bipiramidi transitive per facce.

Caratteristiche

Come suggerito dal nome, questo solido con 10 facce, che risulta essere il poliedro duale del prisma pentagonale, può essere costruito unendo due piramidi pentagonali per le loro basi. Sebbene tutte le sue facce siano congruenti ed essa sia transitiva per facce, la bipiramide pentagonale non è un solido platonico perché sui suoi vertici non incide sempre lo stesso numero di facce, dato che su due di essi ne incidono cinque e sugli altri otto ne incidono quattro.

Nel caso in cui le facce della bipiramide siano tutte triangoli equilateri, allora essa diventa uno dei 92 solidi di Johnson, in particolare il J₁₃, ossia un poliedro strettamente convesso avente come facce dei poligoni regolari ma comunque non appartenente alla famiglia dei poliedri uniformi,^[1] e il fatto che le sue facce siano tutte costituite da triangoli equilateri la rende un deltaedro, in particolare uno degli otto deltaedri strettamente convessi.

La bipiramide pentagonale è 4-connessa, il che significa che è necessario rimuovere 4 dei suoi vertici per disconnettere tutti i vertici rimanenti. Ciò fa di essa uno dei soli quattro poliedri simpliciali ben coperti 4-connessi, il che significa che tutti gli insiemi indipendenti massimali dei suoi vertici hanno la stessa dimensione. Gli altri tre poliedri con questa proprietà sono l'ottaedro regolare, il disfenoide camuso e un poliedro irregolare con 12 vertici e 20 facce triangolari.^[2]

Formule

Considerata una bipiramide pentagonale con tutte le facce regolari e con spigolo di lunghezza $a$ , le seguenti formule consentono di calcolarne il volume $V$ , l'area della superficie $A$ e l'altezza $h$ :

V={\frac {5+{\sqrt {5}}}{12}}a^{3}\approx 0,6030056648\cdot a^{3};

A={\frac {5{\sqrt {3}}}{2}}a^{2}\approx 4,330127019\cdot a^{2};

h={\sqrt {2-{\frac {2}{\sqrt {5}}}}}a\approx 1,0514622242\cdot a.

Poliedro duale

Il poliedro duale della bipiramide pentagonale è, come detto, il prisma triangolare, ossia un prisma con sette facce: due pentagoni regolari paralleli uniti da una serie di cinque rettangoli. Sebbene il prisma pentagonale abbia anche una forma che lo rende un poliedro uniforme, ossia quella in cui le sue facce laterali sono quadrati, il poliedro duale della bipiramide pentagonale ha le facce laterali rettangolari e non è un poliedro uniforme.

Poliedro duale	Sviluppo piano del duale

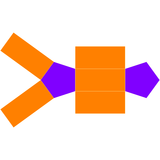
Poliedri correlati

Come gli altri poliedri, anche la bipiramide pentagonale può essere sottoposta a operazione di rettificazione (ossia un troncamento dove gli spigoli sono ridotti della metà), troncamento e levigatura (altrimenti detto anche "addolcimento"). Nella figura sottostante sono rappresentate queste tre operazioni applicate in sequenza al nostro poliedro.

Proiezione su sfera

La proiezione su una sfera di una bipiramide pentagonale sembra la composizione di un osoedro e di un diedro pentagonali, ed è membro di una serie infinita di proiezioni su sfera di composti di coppie di poliedri regolari in posizione duale. In associazione con gli altri membri della serie, la bipiramide pentagonale è talvolta chiamata "decaedro deltoidale" (o "trapezoidale"), sebbene in essa i "deltoidi" siano dei triangoli e non degli aquiloni.

Note

^ Norman W. Johnson, Convex Polyhedra with Regular Faces, in Canadian Journal of Mathematics, vol. 18, Canadian Mathematical Society, 1966, pp. 169-200, DOI:10.4153/CJM-1966-021-8. URL consultato il 14 luglio 2021.
^ Arthur S. Finbow, Bert L. Hartnell, Richard J. Nowakowski e Michael D. Plummer, On well-covered triangulations: Part III, in Discrete Applied Mathematics, vol. 158, n. 8, Elsevier, Aprile 2010, pp. 894-912, DOI:10.1016/j.dam.2009.08.002.

Altri progetti

Wikimedia Commons contiene immagini o altri file su bipiramide pentagonale

Collegamenti esterni

(EN) Eric W. Weisstein, Pentagonal Dipyramid, su MathWorld, Wolfram Research.

Bipiramidi regolari n-gonali:
Bipiramide	Bipiramide digonale	Bipiramide triangolare (Vedi: J₁₂)	Bipiramide quadrata (Vedi: O)	Bipiramide pentagonale (Vedi: J₁₃)	Bipiramide esagonale	Bipiramide ettagonale	Bipiramide ottagonale	Bipiramide ennagonale	Bipiramide decagonale	...	Bipiramide apeirogonale
Immagine del poliedro										...
Immagine della tassellatura sferica										Immagine della tassellatura del piano
Incidenza	V2.4.4	V3.4.4	V4.4.4	V5.4.4	V6.4.4	V7.4.4	V8.4.4	V9.4.4	V10.4.4	...	V∞.4.4
Diagramma di Coxeter-Dynkin										...

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica

[1] Norman W. Johnson, Convex Polyhedra with Regular Faces, in Canadian Journal of Mathematics, vol. 18, Canadian Mathematical Society, 1966, pp. 169-200, DOI:10.4153/CJM-1966-021-8. URL consultato il 14 luglio 2021.

[2] Arthur S. Finbow, Bert L. Hartnell, Richard J. Nowakowski e Michael D. Plummer, On well-covered triangulations: Part III, in Discrete Applied Mathematics, vol. 158, n. 8, Elsevier, Aprile 2010, pp. 894-912, DOI:10.1016/j.dam.2009.08.002.

[1]

[2]