Utente:Grasso Luigi/sandbox4/Piano di Fano

Collineazioni

Una collineazione del piano di Fano corrispondente alla permutazione di un codice Gray a 3 bit

Una collineazione, automorfismo, o simmetria del piano di Fano è una permutazione dei 7 punti che preserva la collinearità: that is, it carries collinear points (on the same line) to collinear points. By the Fundamental theorem of projective geometry, the full collineation group (or automorphism group, or symmetry group) is the projective linear group PGL(3, 2),{{efn|Actually it is PΓL(3, 2), but since the finite field of order 2 has no non-identity automorphisms, this becomes PGL(3, 2) anche denotato PGL₃(F₂). Since the field has only one nonzero element, this group is isomorphic to the projective special linear group PSL(3, 2) and the general linear group GL(3, 2). Ammette isomorfismo anche con PSL(2, 7).

This is a well-known group of order 168 = 2³·3·7, the next non-abelian simple group after A₅ of order 60 (ordered by size).

As a permutation group acting on the 7 points of the plane, the collineation group is doubly transitive meaning that any ordered pair of points can be mapped by at least one collineation to any other ordered pair of points.Template:Sfn (See below.)

Collineations may also be viewed as the color-preserving automorphisms of the Heawood graph (see figure).

F₈ is a degree-three field extension of F₂, so the points of the Fano plane may be identified with F₈ ∖ Template:Mset. The symmetry group may be written PGL(3, 2) = Aut(P²F₂). Similarly, PSL(2, 7) = Aut(P¹F₇). There is a relation between the underlying objects, P²F₂ and P¹F₇ called the Cat's Cradle map. Color the seven lines of the Fano plane ROYGBIV, place your fingers into the two dimensional projective space in ambient 3-space, and stretch your fingers out like the children's game Cat's Cradle. You will obtain a complete graph on seven vertices with seven colored triangles (projective lines). The missing origin of F₈ will be at the center of the septagon inside. Now label this point as ∞, and pull it backwards to the origin. One can write down a bijection from F₇ ∪ Template:Mset to F₈. Set x^∞ = 0 and send the slope k ↦ x^∞ + x^k ∈ F₈ ≅ F₂[x] / (x³ + x + 1), where now x^k labels the vertices of K₇ with edge coloring, noting that F×8 is a cyclic group of order 7. The symmetries of P¹F₇ are Möbius transformations, and the basic transformations are reflections (order 2, k ↦ −1/k), translations (order 7, k ↦ k + 1), and doubling (order 3 since 2³ = 1, k ↦ 2k). The corresponding symmetries on the Fano plane are respectively swapping vertices, rotating the graph, and rotating triangles.

Duality in the Fano plane: Each point corresponds to a line and vice versa.

Dualità

A bijection between the point set and the line set that preserves incidence is called a duality and a duality of order two is called a polarity.

Dualities can be viewed in the context of the Heawood graph as color reversing automorphisms. An example of a polarity is given by reflection through a vertical line that bisects the Heawood graph representation given on the right. The existence of this polarity shows that the Fano plane is self-dual. This is also an immediate consequence of the symmetry between points and lines in the definition of the incidence relation in terms of homogeneous coordinates, as detailed in an earlier section.

Struttura ciclica

Una numerazione tipo nimber del piano di Fano

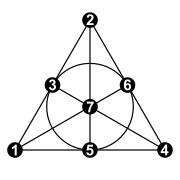
Il gruppo di permutazione dei 7 punti, sottogruppo del gruppo simmetrico di ordine 7, cioè

$\operatorname {Aut} (P^{2}F_{2})\leq S_{7}\quad |F|=168=1+21+42+56+48\quad |S_{7}|=5040$

ha le seguenti 6 classi di coniugazione: 4 strutture cicliche:

• La permutazione identica con tutti 1-ciclo $(1)(2)(3)(4)(5)(6)(7)$
• 21 permutazioni con 2-cicli cioè $(\cdot )(\cdot )(\cdot )(\cdot )(\cdot )(\cdot ~\cdot )$
• 42 permutations with a 4-cycle and a 2-cycle cioè $(\cdot )(\cdot ~\cdot )(\cdot ~\cdot ~\cdot ~\cdot )$
• 56 permutations with two 3-cycles

1 struttura ciclica con ciclo completo o 7-ciclo con 24+24 elementi:

• A maps to B, B to C, C to D. Then D is on the same line as A and B.
• A maps to B, B to C, C to D. Then D is on the same line as A and C.

(See here for a complete list.)

HenceTemplate:How, by the Pólya enumeration theorem, the number of inequivalent colorings of the Fano plane with n colors is

${{n^{7}+21n^{5}+98n^{3}+48n} \over 168}$.

Note

Postille

Bibliografia

• (EN) Burkard Polster, Geometrical Picture Book, Springer, 1998, ISBN 978-0-387-98437-7.
• (EN) J. W. P. Hirschfeld, Projective Geometries Over Finite Fields, OUP, 1979, ISBN 978-0-19-850295-1.