RB-Albero
Un RB-Albero (o anche red-black tree, in italiano albero rosso-nero) è un tipo di albero binario di ricerca bilanciato, una struttura dati usata in Informatica, tipicamente utilizzata per implementare insiemi o array associativi. La struttura originale è stata inventata nel 1972 da Rudolf Bayer che la chiamò "B-alberi binari simmetrici", ma ha acquisito il nome attuale a partire da un articolo del 1978 di Leo J. Guibas e Robert Sedgewick. È complessa, ma ha un eccellente tempo di esecuzione nel caso peggiore ed è molto efficiente: effettua ricerche, inserimenti e cancellazioni in un tempo di , dove è il numero di elementi nell'albero.
Concetti di base e terminologia[modifica | modifica wikitesto]
Un albero rosso-nero è un tipo speciale di albero binario, che è una struttura utilizzata in informatica per organizzare dati comparabili, ad esempio numeri. Ciascuna unità di dati è conservata in un nodo. Uno dei nodi funge sempre da punto di partenza, e non è figlio di nessun nodo; viene di solito chiamato nodo root o semplicemente root. Questo nodo ha al massimo due figli, ovvero altri nodi ai quali è connesso. Ciascuno di questi figli ha a sua volta al massimo due figli, e così via. Il nodo root inoltre ha un path (percorso) che lo collega a qualsiasi altro nodo nell'albero.
Se un nodo non ha figli, viene chiamato nodo foglia, poiché, intuitivamente, fa parte della "periferia" dell'albero. Un sottoalbero è una porzione dell'albero che si estende a partire da un dato nodo. Negli alberi rosso-neri, si assume che le foglie abbiano valore null, ovvero esse non contengono dati.
Poiché gli alberi rosso-neri sono anche alberi binari di ricerca, essi soddisfano il vincolo per cui ogni nodo contiene un valore minore o uguale a quello di tutti i nodi del suo sottoalbero destro, e maggiore o uguale a quello di tutti i nodi del suo sottoalbero sinistro. Ciò rende veloce la ricerca di un dato valore nell'albero, e consente un ordinamento efficiente degli elementi.
Utilizzi e vantaggi[modifica | modifica wikitesto]
Gli alberi rosso-neri, assieme agli alberi AVL, offrono le migliori performance nel caso peggiore dei tempi di ricerca, inserimento e cancellazione. Ciò li rende non soltanto importanti nelle applicazioni sistema real-time, ma fondamentali "mattoni" di altre strutture dati che forniscono garanzie nel caso peggiore; ad esempio, molte strutture dati usate nella geometria computazionale sono basate su alberi rosso-neri.
Gli alberi rosso-neri sono inoltre importanti nella programmazione funzionale, in cui sono una delle strutture dati persistenti più comuni, utilizzati per costruire array associativi e set in grado di mantenere stati precedenti alla modifica. La versione persistente degli alberi rosso-neri richiede uno spazio di O(log n) per ciascun inserimento o cancellazione, in aggiunta al tempo.
Gli alberi rosso-neri sono un'isometria degli alberi 2-3-4. In altre parole, per ciascun albero 2-3-4, esiste almeno un albero rosso-nero con gli elementi nello stesso ordine. Le operazioni di inserimento e cancellazione sugli alberi 2-3-4 sono equivalenti a quelle di ricolorazione e rotazione negli alberi rosso-neri. Gli alberi 2-3-4, dunque, sono uno strumento importante per comprendere la logica esistente dietro gli alberi rosso-neri, ed è questo il motivo per cui molti testi sugli algoritmi introducono gli alberi 2-3-4 subito prima di quelli rosso-neri, benché quelli 2-3-4 non vengano quasi mai utilizzati nella pratica.
Proprietà[modifica | modifica wikitesto]

Un albero rosso-nero è un albero binario di ricerca in cui ciascun nodo ha un attributo colore, il cui valore può essere rosso oppure nero. In aggiunta ai requisiti ordinari per un albero binario di ricerca, un albero rosso-nero soddisfa le seguenti proprietà:
- Ogni nodo ha colore rosso o nero.
- Il nodo root inizialmente è nero.
- Ogni foglia è nera e contiene elemento null;
- Entrambi i figli di ciascun nodo rosso sono neri;
- Ogni cammino da un nodo a una foglia nel suo sottoalbero contiene lo stesso numero di nodi neri.
Questi vincoli rafforzano una proprietà critica degli alberi rosso-neri: che il cammino più lungo dal nodo root a una foglia è al massimo lungo il doppio del cammino più breve. Ne risulta dunque un albero fortemente bilanciato. Poiché le operazioni di ricerca di un valore, inserimento e cancellazione richiedono un tempo di esecuzione nel caso peggiore proporzionale all'altezza dell'albero, questo limite superiore teorico sull'altezza rende gli alberi rosso-neri molto efficienti nel caso peggiore, al contrario di quanto accade con gli ordinari alberi binari di ricerca.
Per vedere in che modo tali proprietà vengono garantite, è sufficiente notare che nessun cammino può avere due nodi rossi in fila, per la proprietà 4. Il cammino più breve possibile ha tutti nodi neri, e il più lungo alterna nodi rossi e nodi neri. Poiché tutti i cammini massimi hanno lo stesso numero di nodi neri, per la proprietà 5, ciò dimostra che nessun cammino è lungo più del doppio di qualsiasi altro cammino.
In molte strutture dati "alberi", è possibile che un nodo abbia un solo figlio, e che i nodi foglia contengano dati. È possibile presentare anche gli alberi rosso-neri secondo questo paradigma, ma ciò modificherebbe alcune delle proprietà e complicherebbe l'algoritmo. Per questa ragione, in questo articolo parliamo di "foglie nulle", che non contengono dati e servono semplicemente ad indicare dove finisce l'albero. Questi nodi vengono spesso omessi nella rappresentazione grafica, e l'albero rappresentato sembra contraddire i principi esposti, ma di fatto non è così. La conseguenza è che tutti i nodi interni (non foglia) hanno due figli, sebbene uno o entrambi questi figli possano essere una foglia nulla.
Alcune trattazioni illustrano gli alberi rosso-neri come alberi binari di ricerca i cui archi (invece dei nodi) sono colorati di rosso o di nero; ma ciò non fa alcuna differenza. Nella nostra terminologia, il colore di un nodo corrisponde al colore dell'arco che connette il nodo al padre, escluso il nodo root che è sempre nero (proprietà 2) in considerazione del fatto che l'arco corrispondente non esiste.
Operazioni[modifica | modifica wikitesto]
Le operazioni di lettura su un albero rosso-nero non richiedono modifiche rispetto a quelle utilizzate per gli alberi binari di ricerca, poiché gli alberi rosso-neri sono una loro specializzazione. Al contrario, il risultato immediato di un inserimento o di una cancellazione può violare le proprietà dell'albero rosso-nero, e ristabilire tali proprietà richiede un piccolo numero (O(log n) o O(1) ammortizzato) di ricolorazioni (che sono molto veloci nella pratica) e non più di tre rotazioni dell'albero (due per l'inserimento). Nonostante l'inserimento e la cancellazione siano operazioni complicate, i loro tempi di esecuzione rimangono dell'ordine di O(log n).
Inserimento[modifica | modifica wikitesto]
Si comincia aggiungendo un nodo come se si trattasse di un albero binario di ricerca classico, e colorandolo di rosso. Il passo successivo dipende dal colore degli altri nodi attigui. Useremo il termine nodo zio per riferirci al fratello del nodo padre. Si noti che:
- la proprietà 3 (tutte le foglie, incluse quelle nulle, sono nere) persiste;
- la proprietà 4 (entrambi i figli di ogni nodo rosso sono neri) è minacciata soltanto dall'inserimento di un nodo rosso, dalla ricolorazione in rosso di un nodo nero, o da una rotazione;
- la proprietà 5 (tutti i cammini a partire da un dato nodo verso le sue foglie contengono lo stesso numero di nodi neri) è minacciata soltanto dall'inserimento di un nodo nero, dalla ricolorazione in nero di un nodo rosso, o da una rotazione.
- Nota: utilizzeremo la seguente simbologia: N per il nodo inserito, P per il nodo padre di N, G per il nodo padre di P, e U per il "nodo zio" di N. Si noti che in qualche caso è possibile che ruoli e simboli dei nodi vengano scambiati; in ogni caso, ciascun simbolo continua a rappresentare lo stesso nodo che rappresentava all'inizio del caso.
Ciascun caso viene dimostrato con del codice d'esempio in linguaggio C, i nodi "zio" e "nonno" si trovano tramite le seguenti funzioni:
node grandparent(node n) {
return n->parent->parent;
}
node uncle(node n) {
if (n->parent == grandparent(n)->left)
return grandparent(n)->right;
else
return grandparent(n)->left;
}
- Caso 1
- il nuovo nodo N è nella root dell'albero. In questo caso, viene colorato di nero per soddisfare la proprietà 2 (la root è nera). Poiché questo inserimento aggiunge un nodo nero a ciascun cammino, la proprietà 5 (tutti i cammini a partire da un dato nodo verso le sue foglie contengono lo stesso numero di nodi neri) non è violata.
void insert_case1(node n) {
if (n->parent == NULL)
n->color = BLACK;
else
insert_case2(n);
}
- Caso 2
- il padre P del nuovo nodo è nero, quindi la proprietà 4 (entrambi i figli di ogni nodo rosso sono neri) non è invalidata. In questo caso, l'albero è ancora valido. La proprietà 5 (tutti i cammini a partire da un dato nodo verso le sue foglie contengono lo stesso numero di nodi neri) sembrerebbe minacciata, perché il nuovo nodo N ha due foglie nere, ma poiché N è rosso, i cammini attraverso ognuno dei suoi figli hanno lo stesso numero di nodi neri poiché sono cammini separati, per cui la proprietà rimane soddisfatta.
void insert_case2(node n) {
if (n->parent->color == BLACK)
return; /* Tree is still valid */
else
insert_case3(n);
}
- Nota: nei casi che seguono si assume che N abbia un nodo "nonno" G, perché il padre P è rosso, e se fosse stato root sarebbe stato nero. Inoltre, N ha anche un nodo "zio" U, sebbene esso possa essere una foglia nei casi 4 e 5.
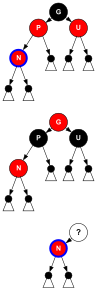
- Caso 3
- se sia il padre P sia lo zio U sono rossi, allora è possibile ricolorare entrambi di nero e ricolorare di rosso il nonno G per mantenere la proprietà 5 (tutti i cammini a partire da un dato nodo verso le sue foglie contengono lo stesso numero di nodi neri). Adesso il nuovo nodo N ha un padre nero. Poiché qualsiasi cammino attraverso il padre o lo zio deve passare attraverso il nonno, il numero di nodi neri su questi cammini non cambia. Però il nonno G ora potrebbe violare la proprietà 2 (il nodo root è nero) o la 4 (entrambi i figli di ogni nodo rosso sono neri) perché potrebbe avere un padre rosso. Per risolvere il problema, la procedura va ripetuta ricorsivamente su G a partire dal caso 1. Si noti che questa è l'unica chiamata ricorsiva, e che avviene prima di qualsivoglia rotazione, il che prova che si avrà un numero costante di rotazioni.
void insert_case3(node n) {
if (uncle(n) != NULL && uncle(n)->color == RED) {
n->parent->color = BLACK;
uncle(n)->color = BLACK;
grandparent(n)->color = RED;
insert_case1(grandparent(n));
}
else
insert_case4(n);
}
- Nota: nei casi seguenti, si assume che il nodo padre P è figlio sinistro del proprio padre. Se fosse figlio destro, left e right dovrebbero essere invertiti nei casi 4 e 5.

- Caso 4
- il padre P è rosso ma lo zio U è nero; il nuovo nodo N è il figlio destro di P, e P a sua volta è figlio sinistro di G. In questo caso, si effettua una rotazione a sinistra che scambia i ruoli del nuovo nodo N e del padre P; quindi ci si occupa dell'ex nodo padre P utilizzando il caso 5 (scambiando i nomi N e P). Ciò fa sì che alcuni cammini (quelli etichettati con "1" nel grafico) passino ora attraverso il nuovo nodo senza che prima ciò accadesse; ma entrambi questi nodi sono rossi, perciò la proprietà 5 (tutti i cammini a partire da un dato nodo verso le sue foglie contengono lo stesso numero di nodi neri) non è violata. La proprietà 4 (entrambi i figli di ogni nodo rosso sono neri) è ancora violata, ma si può risolvere continuando con il caso 5.
void insert_case4(node n) {
if (n == n->parent->right && n->parent == grandparent(n)->left) {
rotate_left(n->parent);
n = n->left;
} else if (n == n->parent->left && n->parent == grandparent(n)->right) {
rotate_right(n->parent);
n = n->right;
}
insert_case5(n);
}

- Caso 5
- il padre P è rosso ma il nonno G e lo zio U sono neri, il nuovo nodo N è il figlio sinistro di P, e P è il figlio sinistro di G. In questo caso, si effettua una rotazione a destra su G; il risultato è un albero in cui l'ex padre P è ora il padre sia del nuovo nodo N sia dell'ex nonno G. Sappiamo che G è nero, perché altrimenti il suo ex figlio P non sarebbe potuto essere rosso. Si scambiano dunque i colori di P e G, e l'albero che ne risulta soddisfa la proprietà 4 (entrambi i figli di ogni nodo rosso sono neri). La proprietà 5 (tutti i cammini a partire da un dato nodo verso le sue foglie contengono lo stesso numero di nodi neri) resta a sua volta soddisfatta, poiché tutti i cammini che prima attraversavano uno di questi tre nodi passavano prima attraverso G , ora attraverso P. In ogni caso, è il solo nodo nero dei tre.
void insert_case5(node n) {
n->parent->color = BLACK;
grandparent(n)->color = RED;
if (n == n->parent->left && n->parent == grandparent(n)->left) {
rotate_right(grandparent(n));
} else {
/* Here, n == n->parent->right && n->parent == grandparent(n)->right */
rotate_left(grandparent(n));
}
}
Si noti che tutte le chiamate nel codice utilizzano la ricorsione in coda.
Cancellazione[modifica | modifica wikitesto]
In un normale albero binario di ricerca, quando si cancella un nodo che ha due figli non-foglia, ci si può trovare in due situazioni: o il valore massimo si trova nel suo sottoalbero sinistro o il valore minimo si trova nel suo sottoalbero destro, quindi si sposta tale valore nel nodo che si vuole cancellare. A questo punto si cancella il nodo da cui abbiamo copiato il valore, di cui si devono avere meno di due figli non-foglia. Poiché copiare semplicemente un valore non viola nessuna proprietà rosso-nera, il problema si riduce a quello di cancellare un nodo con al massimo un figlio. Non importa se il nodo è quello che si voleva eliminare inizialmente o il nodo di cui si è copiato il valore.
Se si sta cancellando un nodo rosso, lo si sostituisce semplicemente con suo figlio, che dev'essere nero. Tutti i cammini che attraversavano il nodo cancellato adesso passeranno attraverso un nodo rosso in meno, e sia il padre che il figlio del nodo cancellato devono essere neri, perciò le proprietà 3 (tutte le foglie, incluse quelle nulle, sono nere) e 4 (entrambi i figli di ogni nodo rosso sono neri) sono ancora valide. Un altro caso semplice è quando il nodo cancellato è nero e suo figlio è rosso. La cancellazione di un nodo nero potrebbe violare le proprietà 4 (entrambi i figli di ogni nodo rosso sono neri) e 5 (tutti i cammini a partire da un dato nodo verso le sue foglie contengono lo stesso numero di nodi neri), ma se si ricolora il figlio di nero, entrambe le proprietà sono mantenute.
Il caso complesso è quando sia il nodo da cancellare sia il figlio sono neri. Il primo passo è sostituire il nodo da eliminare con il figlio. Si chiamerà quindi N il figlio nella nuova posizione e S suo fratello (l'altro figlio del suo nuovo padre). Nel diagramma qui sotto, noi useremo anche P per indicare il nuovo padre di N, e si N è figlio sinistro, C come figlio sinistro di S e D per il figlio destro; si N è figlio destro, C come figlio destro di S e D per il figlio sinistro. (È chiaro che S non può essere una foglia.)
- Attenzione: tra i due casi, scambiamo ruoli e label dei nodi, ma in ogni caso, ogni label continua a rappresentare lo stesso nodo che rappresentava all'inizio del caso. Qualsiasi colore mostrato nel diagramma è supposto o implicato dalle precedenti ipotesi. Il bianco rappresenta un colore sconosciuto (indifferentemente rosso o nero).
Troveremo i fratelli usando questa funzione:
node sibling(node n) {
if (n == n->parent->left)
return n->parent->right;
else
return n->parent->left;
}
Possiamo svolgere i passi descritti sopra con l'uso del seguente codice, dove la funzione replace_node sostituisce child nella posizione n dell'albero. Per convenienza, il codice presentato in questa sezione presupporrà che le foglie nulle siano rappresentate da oggetti nodo, piuttosto che da NULL (il codice della sezione Inserimento funziona in entrambi i casi).
void delete_one_child(node n) {
/* Si assume che n ha al massimo un figlio non nullo */
node child = (is_leaf(n->right)) ? n->left: n->right;
replace_node(n, child);
if (n->color == BLACK) {
if (child->color == RED)
child->color = BLACK;
else
delete_case1(child);
}
free(n);
}
- Attenzione: Se N è una foglia nulla e non la vogliamo rappresentare come oggetto nodo, possiamo modificare l'algoritmo chiamando prima delete_case1() sul padre (il nodo che vogliamo cancellare,
nnel codice riportato sopra) e cancellarlo dopo. Possiamo farlo perché il padre è nero, quindi si comporta allo stesso modo di una foglia nulla (chiamata a volte foglia 'fantasma'). E possiamo cancellarlo senza rischi alla fine, visto chenrimarrà foglia dopo tutte le operazioni, come mostrato sopra.
Se sia N che il padre originale sono neri, cancellare il padre farà in modo che i percorsi attraverso N abbiano un nodo nero in meno rispetto ai percorsi che non ci passano. Dal momento che questa situazione violerebbe la proprietà 5 (Tutti i percorsi da un qualsiasi nodo alle foglie sottostanti contengono lo stesso numero di nodi neri), l'albero deve essere ribilanciato. Ci sono molti casi da considerare.
- Caso 1
- N è la nuova root. In questo caso, abbiamo finito. Abbiamo rimosso un nodo nero da ogni percorso, e la nuova root è nera, quindi tutte le proprietà sono soddisfatte.
void delete_case1(node n) {
if (n->parent == NULL)
return;
else
delete_case2(n);
}
- Attenzione: Nei casi 2, 5, e 6, supponiamo che N sia il figlio sinistro del proprio padre P. Se fosse il figlio destro, destro e sinistro andrebbero invertiti nel seguito della discussione. Di nuovo, il codice di esempio tiene conto di entrambi i casi.

- Caso 2
- S è rosso. In questo caso invertiamo i colori di P e S, ed effettuiamo una rotazione a sinistra su P, facendo ruotare S nel nonno di N. Notare che P deve essere nero, visto che ha un figlio rosso. Nonostante tutti i percorsi abbiano lo stesso numero di nodi neri, ora N ha un fratello nero ed un padre rosso, quindi possiamo procedere con i passi 4, 5, o 6 (il nuovo fratello è nero perché era una volta il figlio del rosso S). Nell'ultimo caso, rietichettiamo S come nuovo fratello di N.
void delete_case2(node n) {
if (sibling(n)->color == RED) {
n->parent->color = RED;
sibling(n)->color = BLACK;
if (n == n->parent->left)
rotate_left(n->parent);
else
rotate_right(n->parent);
}
delete_case3(n);
}

- Caso 3
- P, S, ed il figlio di S sono neri. In questo caso, semplicemente ricoloriamo S di rosso. Il risultato è che tutti i percorsi che passano da S, ovvero tutti quelli non passanti da N, hanno un nodo nero in meno. Visto che cancellare il padre originale di N toglie un nodo nero ai percorsi che passano da N, le cose sono aggiustate. Comunque, tutti i percorsi che passano da P ora hanno un nero in meno di quelli che non ci passano, quindi la proprietà 5 (Tutti i percorsi da un qualsiasi nodo alle foglie sottostanti contengono lo stesso numero di nodi neri) è ancora violata. Per correggere questo problema rieseguiamo la bilanciatura su P, ripartendo dal caso 1.
void delete_case3(node n) {
if (n->parent->color == BLACK &&
sibling(n)->color == BLACK &&
sibling(n)->left->color == BLACK &&
sibling(n)->right->color == BLACK)
{
sibling(n)->color = RED;
delete_case1(n->parent);
}
else
delete_case4(n);
}
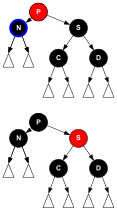
- Caso 4
- S ed il suo figlio sono neri, ma P è rosso. In questo caso scambiamo i colori di S e P. Questa mossa non modifica il numero di neri nei percorsi che non passano da N, ma ne aggiunge uno a quelli che ci passano, permettendo la cancellazione di un nodo nero in quei percorsi.
void delete_case4(node n) {
if (n->parent->color == RED &&
sibling(n)->color == BLACK &&
sibling(n)->left->color == BLACK &&
sibling(n)->right->color == BLACK)
{
sibling(n)->color = RED;
n->parent->color = BLACK;
}
else
delete_case5(n);
}
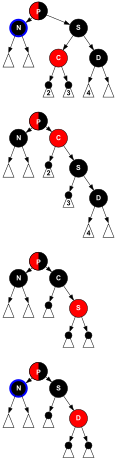
- Caso 5
- S è nero, il figlio sinistro di S è rosso, quello destro è nero, e N è il figlio sinistro del proprio padre. In questo caso ruotiamo a destra su S, in modo che il figlio sinistro di S ne diventi il padre, ed N il nuovo fratello. Scambiamo i colori di S e del suo nuovo padre. Tutti i percorsi hanno ancora lo stesso numero di nodi neri, ma ora N ha un fratello nero il cui figlio destro è rosso, così ricadiamo nel caso 6. Né N né il suo padre vengono modificati da questa trasformazione.
(Ancora, per il caso 6, rietichettiamo S come nuovo fratello di N).
void delete_case5(node n) {
if (n == n->parent->left &&
sibling(n)->color == BLACK &&
sibling(n)->left->color == RED &&
sibling(n)->right->color == BLACK)
{
sibling(n)->color = RED;
sibling(n)->left->color = BLACK;
rotate_right(sibling(n));
}
else if (n == n->parent->right &&
sibling(n)->color == BLACK &&
sibling(n)->right->color == RED &&
sibling(n)->left->color == BLACK)
{
sibling(n)->color = RED;
sibling(n)->right->color = BLACK;
rotate_left(sibling(n));
}
delete_case6(n);
}

- Caso 6
- S è nero, il suo figlio destro è rosso, e N è il figlio sinistro del proprio padre P. In questo caso effettuiamo una rotazione a sinistra su P, in modo che S diventi padre di P e del figlio destro di S. Scambiamo i colori di P e S, e coloriamo il figlio destro di S di nero. Il sottoalbero avrà lo stesso colore della propria root, cosicché le proprietà 4 (Entrambi i figli di un nodo rosso sono neri) e 5 (Tutti i percorsi da un qualsiasi nodo alle foglie sottostanti contengono lo stesso numero di nodi neri) non vengono violate. Comunque, N ha un antenato nero in più: sia che P sia divento nero, sia che era nero e S è stato aggiunto come nonno nero. Per cui i percorsi che attraversano N incontrano un nero in più.
Contemporaneamente, se un percorso non attraversa N, ci sono due possibilità:
- Attraversa il nuovo fratello di N. Per cui deve attraversare S e P, sia prima che dopo le modifiche, che si sono semplicemente scambiati il colore (ovvero il numero di neri non è cambiato).
- Attraversa il nuovo zio di N, figlio destro di S. In questo caso, prima attraversava S, il padre di S, ed il figlio destro di S, ma ora attraversa solo S, che ha preso il colore dell'ex padre, ed il figlio destro di S, modificato da rosso a nero. Il risultato è che il numero di neri non è cambiato.
In ogni caso, il numero di nodi neri su questi percorsi non cambia. Per cui abbiamo ristabilito le proprietà 4 (Entrambi i figli di un nodo rosso sono neri) e 5 (Tutti i percorsi da un qualsiasi nodo alle foglie sottostanti contengono lo stesso numero di nodi neri). Il nodo bianco, nel diagramma, può essere rosso o nero, l'importante è che abbia lo stesso colore prima e dopo la trasformazione.
void delete_case6(node n) {
sibling(n)->color = n->parent->color;
n->parent->color = BLACK;
if (n == n->parent->left) {
/* Here, sibling(n)->right->color == RED */
sibling(n)->right->color = BLACK;
rotate_left(n->parent);
}
else
{
/* Here, sibling(n)->left->color == RED */
sibling(n)->left->color = BLACK;
rotate_right(n->parent);
}
}
Di nuovo, la funzione utilizza una ricorsione di coda (tail recursion), cosicché l'algoritmo è ancora in-place. Inoltre, nessuna chiamata ricorsiva viene fatta dopo una rotazione, il che rende costante il numero di rotazione (massimo 3).
Dimostrazione dei limiti asintotici[modifica | modifica wikitesto]
Un albero rosso-nero che ha nodi interni ha un'altezza .
Definizioni:
- = altezza del sottoalbero avente radice in .
- = il numero di nodi neri (non contando se è nero) da a qualsiasi foglia nel sottoalbero (chiamata altezza nera).
Lemma: Un sottoalbero avente radice in v ha almeno nodi interni.
Dimostrazione del lemma (per induzione):
Assunto:
Se ha altezza zero deve essere vuoto, quindi . Per cui:
Ipotesi Induttiva: tale che , ha nodi interni implica che tale che ha nodi interni.
Dal momento che ha è un nodo interno. Ha due figli la cui altezza-nera è bh() o (a seconda che sia rosso o nero). Per ipotesi induttiva ogni figlio ha almeno nodi interni, per cui ha:
nodi interni.
Usando questo lemma possiamo dimostrare che l'altezza dell'albero è logaritmica. Dato che almeno la metà dei nodi di qualsiasi percorso dalla radice ad una foglia sono neri (proprietà 4 di un albero rosso-nero), l'altezza nera della radice è almeno h(root)/2. Dal lemma otteniamo:
Quindi l'altezza della radice è .
Estensione di RB-Alberi[modifica | modifica wikitesto]
L'estensione di un RB-Albero è una pratica che consiste nell'aggiungere ai nodi informazioni aggiuntive, che consentano di supportare efficientemente altre operazioni oltre a quelle standard.
Gli alberi di selezione T (o order-statistic trees), per esempio, sono alberi rosso-neri che memorizzano in ogni nodo x la dimensione del sottoalbero radicato in x stesso (foglie escluse). Come risultato sono in grado di ricercare un elemento con un dato rango, o determinare il rango di un elemento dato, con una complessità O(log n) nel caso pessimo[1].
Gli Wise Red-Black Trees garantiscono invece più efficienza nel trattare blocchi di elementi contigui. Hanno una struttura simile agli alberi di selezione T, ma i nodi memorizzano solo la dimensione del sottoalbero sinistro. Si distinguono maggiormente per le modalità di esecuzione delle operazioni principali[2].
Note[modifica | modifica wikitesto]
- ^ Cormen, Thomas H.; Leiserson, Charles E.; Rivest, Ronald L.; Stein, Clifford, Introduction to Algorithms, 3ª ed., MIT Press, 2009 [1990], ISBN 978-0-262-03384-8.
- ^ Alberto Boffi, An efficient way to manage blocks of data with Wise Red-Black Trees, Giugno 2021.
Bibliografia[modifica | modifica wikitesto]
- (EN) San Diego State University: CS 660: Appunti sugli alberi rosso-neri, di Roger Whitney
- (EN) Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, e Clifford Stein. Introduction to Algorithms, Second Edition. MIT Press and McGraw-Hill, 2001. ISBN 0-262-03293-7. Capitolo 13: Alberi Rosso-Neri, pp. 273 – 301.
Altri progetti[modifica | modifica wikitesto]
 Wikimedia Commons contiene immagini o altri file sull'RB-Albero
Wikimedia Commons contiene immagini o altri file sull'RB-Albero
Collegamenti esterni[modifica | modifica wikitesto]
Dimostrazioni[modifica | modifica wikitesto]
- Animazione di albero rosso-nero, dimostrazione del caso pessimo di inserimento
- aiSee: Algoritmo di ordinamento, GIF animata che mostra l'inserimento (200KB)
Implementazioni[modifica | modifica wikitesto]
- RBT: Libreria per alberi rosso-neri, su efsa.sourceforge.net. URL consultato il 10 settembre 2006 (archiviato dall'url originale il 7 ottobre 2017).
- libredblack: Libreria C per alberi rosso-neri, su libredblack.sourceforge.net.
- Altra implementazione C, su web.mit.edu. URL consultato il 10 settembre 2006 (archiviato dall'url originale il 14 febbraio 2008).
- Implementazione con codice Java in java.util.TreeMap, su javaresearch.org. URL consultato il 10 settembre 2006 (archiviato dall'url originale il 20 ottobre 2007).


















