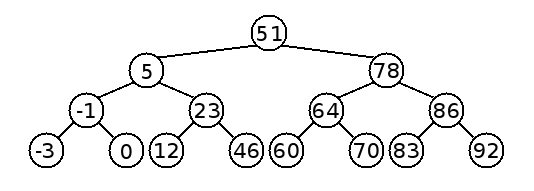
Albero binario di ricerca

Un albero binario di ricerca (meglio noto come BST, dall'inglese Binary Search Tree), in informatica, è un particolare tipo di struttura dati. Permette di effettuare in maniera efficiente operazioni come: ricerca, inserimento e cancellazione di elementi.
Definizione[modifica | modifica wikitesto]
Intuitivamente, un albero binario di ricerca ha le seguenti proprietà:
- Il sottoalbero sinistro di un nodo contiene soltanto i nodi con chiavi minori della chiave del nodo
- Il sottoalbero destro di un nodo contiene soltanto i nodi con chiavi maggiori della chiave del nodo
- Il sottoalbero destro e il sottoalbero sinistro devono essere entrambi due alberi binari di ricerca.
La definizione formale di un albero binario di ricerca è quella di un albero binario avente le seguenti tre proprietà, in cui si indica con la chiave (il valore) di un nodo :
- dove è un insieme parzialmente ordinato
- dove rappresenta il sottoalbero sinistro di un nodo
- dove rappresenta il sottoalbero destro di un nodo
Implementazione[modifica | modifica wikitesto]
In generale, l'implementazione di un albero binario di ricerca è uguale a quella di un albero binario, poiché la differenza tra le due strutture dati è data soltanto dalla distribuzione delle chiavi.
Ad esempio, in C l'implementazione di un albero binario di ricerca contenente dei semplici interi è uguale a quella di un albero binario contenente semplici interi:
struct node
{
int key;
struct node *p;
struct node *left;
struct node *right;
};
Complessità[modifica | modifica wikitesto]
| Complessità al caso pessimo | Complessità al caso medio | |
|---|---|---|
| Spazio | ||
| Ricerca | ||
| Inserimento | ||
| Cancellazione |
Operazioni[modifica | modifica wikitesto]
Per le operazioni più comuni su un albero binario di ricerca contenente nodi, sfruttando anche le sue proprietà, sono stati trovati algoritmi con complessità nell'ordine di con pari all'altezza dell'albero stesso, tranne che per la visita di tutti i nodi (svolta in complessità ).
Essendo l'albero binario di ricerca un particolare tipo di albero binario, nel caso migliore si ha dove è il numero di nodi dell'albero.
Ricerca del minimo[modifica | modifica wikitesto]
Tree_minimum(x)
while(x.left != NULL)
x = x.left;
return x;
Ricerca del massimo[modifica | modifica wikitesto]
Tree_maximum(x)
while(x.right != NULL)
x = x.right;
return x;
Inserimento di un elemento[modifica | modifica wikitesto]
L'inserimento di un elemento in un albero binario di ricerca deve essere fatta in maniera che l'albero risultante dopo l'inserimento rispetti sempre le proprietà strutturali e del contenuto.
L'algoritmo è simile a quello della ricerca. In pratica si svolge una ricerca fin quando non si esce dall'albero e l'ultimo nodo attraversato prima di uscire sarà il padre del nuovo elemento inserito. A questo punto si confronta il valore del padre con quello da inserire e si inserisce adeguatamente a sinistra o destra del padre il nuovo valore.
L'algoritmo ha quindi la stessa complessità algoritmica di quello di ricerca, e quindi con la profondità dell'albero.
Un'implementazione d'esempio in pseudocodice è la seguente:
Tree_insert(T, z) {
y = NULL;
x = T.root; //T.root indica la radice dell'albero T
while(x != NULL) {
y = x; //y è l'ultimo nodo visitato
if(z.key <= x.key) x = x.left;
else x = x.right;
}
z.p = y; //z.p indica il padre del nodo z
if(y == NULL) T.root = z;
else if(z.key <= y.key) y.left = z;
else y.right = z;
}
Cancellazione di un elemento[modifica | modifica wikitesto]
La cancellazione di un elemento in un albero binario di ricerca non è un'operazione semplice. Per mantenere le sue proprietà anche dopo la cancellazione, bisogna distinguere 3 casi differenti.
L'algoritmo per la cancellazione di un elemento distingue i seguenti tre casi:
- Se il nodo è una foglia senza figli, basta cancellarlo dall'albero.
- Se il nodo invece ha un figlio solo, si elimina sostituendolo nella struttura dell'albero con il suo unico figlio.
- Se il nodo invece ha due figli si ricerca il suo successore, e si scambia i valori del nodo da cancellare e del successore trovato, cancellando poi solo quest'ultimo (che ha zero o un figlio solo).
L'operazione di cancellazione ha una complessità finale dove è la profondità dell'albero.
Una implementazione dell'algoritmo in pseudocodice è la seguente:
Transplant(T, u, v)
if(u.p == NULL) T.root = v;
else if(u == u.p.left) u.p.left = v;
else u.p.right = v;
if(v != NULL) v.p = u.p;
Tree_delete(T, z)
if(z.left == NULL) Transplant(T, z, z.right);
else if(z.right == NULL) Transplant(T, z, z.left);
else
y = Tree_minimum(z.right);
if(y.p != z)
Transplant(T, y, y.right);
y.right = z.right;
y.right.p = y;
Transplant(T, z, y);
y.left = z.left;
y.left.p = y;
Visita[modifica | modifica wikitesto]
La visita è un'operazione che permette di esplorare tutti i nodi di un albero che discendono dalla radice. Esistono tre tipi di visita:
- Visita anticipata (o pre-visita/prefissa, corrispettivo di prefix)
- Visita simmetrica (o in-visita/infissa, corrispettivo di infix)
- Visita posticipata (o post-visita/postfissa, corrispettivo di postfix)
Poiché tutti i nodi vengono visitati una sola volta, la complessità algoritmica è pari a .
Una implementazione d'esempio in pseudocodice di visita simmetrica è la seguente:
In_visita(x)
if(x != NULL)
Visita(x.left);
stampa x.key;
Visita(x.right);
Gli altri due tipi di visita sono del tutto simili e differiscono soltanto per la posizione del comando di stampa della chiave; nel caso della visita anticipata la stampa della chiave avviene prima delle due operazioni di visita a sinistra e a destra, mentre nella visita posticipata essa avviene alla fine.
Ricerca di un elemento[modifica | modifica wikitesto]
La ricerca del nodo contenente un certo valore è una delle operazioni più frequenti su un albero binario di ricerca.
L'algoritmo di ricerca, espresso in forma iterativa, sfrutta le caratteristiche dell'albero e l'ordinamento delle chiavi per effettuare tale operazione in maniera efficiente. Esso funziona in maniera analoga alla ricerca binaria: confronta la chiave della radice dell'albero con quella da trovare e, finché non viene trovata, continua a svolgere la ricerca nel sottoalbero sinistro o destro, a seconda della chiave da cercare.
L'algoritmo a ogni passo ricorsivo scende un livello dell'albero, quindi è evidente che la sua complessità algoritmica è , dove è la profondità dell'albero.
Una implementazione dell'algoritmo in pseudocodice è la seguente:
Tree_search(x, k)
while(x != NULL && x.key != k)
if(k < x.key) x = x.left;
else x = x.right;
return x;
Implementare gli alberi di ricerca binari su array[modifica | modifica wikitesto]
Se non è necessario effettuare frequentemente operazioni di inserimento e cancellazioni o non è affatto necessario effettuarle e non si vuole usare troppa memoria è possibile implementare un albero di ricerca binario su un array ordinato, con la restrizione che il numero degli elementi sia con .
L'immagine sopra mostra un albero di ricerca binario implementato su un array ordinato di 15 elementi, si comincia ponendo il centro dell'array come radice dell'albero e come sue foglie rispettivamente il centro della parte destra dell'array e il centro della parte sinistra dell'array, si continua applicando ricorsivamente il procedimento fino a che non sono stati coperti tutti gli elementi. Si ottiene quindi l'equivalente dell'albero:
L'algoritmo in pseudocodice per la ricerca di una chiave è il seguente:
Ricerca di una chiave
N = numero di elementi dell'albero (2^k-1)
A = array delle N chiavi ordinate in ordine crescente, A[0], A[1] .. A[N - 1]
key = chiave da cercare
jump = (N + 1)/4
i = (N - 1)/2
while p > 0 do
if key == A[i] then
ricerca finita
else if key < A[i] then
i = i - jump
else if key > A[i] then
i = i + jump
endif
jump = jump / 2
done
nessun risultato
Bibliografia[modifica | modifica wikitesto]
- Thomas Cormen, Charles E. Leiserson, Ronald Rivest, Introduction, in Introduction to Algorithms, 2ª ed., Cambridge, Massachusetts, The MIT Press, 1998.
Altri progetti[modifica | modifica wikitesto]
 Wikibooks contiene testi o manuali sull'albero binario di ricerca
Wikibooks contiene testi o manuali sull'albero binario di ricerca Wikimedia Commons contiene immagini o altri file sull'albero binario di ricerca
Wikimedia Commons contiene immagini o altri file sull'albero binario di ricerca
Collegamenti esterni[modifica | modifica wikitesto]
- Balanced BST on array Descrizione generale di un metodo di implementazione di un albero binario di ricerca bilanciato, ottimizzato su array