Involuta

In matematica, date due curve $\gamma$ e $\delta$ , si dice che $\delta$ è involuta (o evolvente) di $\gamma$ , o che $\gamma$ è evoluta di $\delta$ , se $\delta$ appartiene allo spazio generato dal vettore tangente di $\gamma$ per ogni punto del dominio e se gli spazi 1-dimensionali generati dai vettori tangenti di $\gamma$ e $\delta$ siano ortogonali in tutto il loro dominio. Per esempio la curva dei centri dei cerchi osculatori di $\gamma$ è un’evoluta di $\gamma$ .

Geometricamente, un'involuta, è un particolare tipo di curva che dipende da un'altra forma o curva. L'involuta di una curva è il luogo dei punti toccati dall'estremo di un pezzo di corda tesa mentre viene avvolta (o srotolata, in modo geometricamente equivalente) attorno alla curva data.^[1]

Le involute appartengono alla famiglia di curve chiamate roulette.

L'evoluta di un'involuta è quindi la curva originaria.

Le nozioni di involuta e di evoluta di una curva furono introdotte da Christiaan Huygens nel suo lavoro intitolato Horologium oscillatorium sive de motu pendulorum ad horologia aptato dimostrationes geometricae (1673).^[2]

Involuta di una curva parametrizzata

Sia ${\vec {c}}(t),\;t\in [t_{1},t_{2}]$ una curva regolare sul piano con curvatura mai nulla e $a\in (t_{1},t_{2})$ , allora la curva con la rappresentazione parametrica

{\vec {C}}_{a}(t)={\vec {c}}(t)-{\frac {{\vec {c}}'(t)}{|{\vec {c}}'(t)|}}\;\int _{a}^{t}|{\vec {c}}'(w)|\;dw

è un'involuta della curva data.

Dimostrazione

Aggiungendo di un numero arbitrario ma fisso $l_{0}$ all'integrale $\int _{a}^{t}|{\vec {c}}'(w)|\;dw,$ risulta in un'involuta corrispondente a una corda estesa di $l_{0}$ (come una palla di filo si lana, avente una certa lunghezza di filo già appeso prima che sia svolto). Quindi, l'involuta può variare di una costante $a$ e/o aggiungendo un numero all'integrale (vedi involuta di una parabola semicubica).

Se ${\vec {c}}(t)=(x(t),y(t))^{T}$ si ottiene

{\begin{aligned}X(t)&=x(t)-{\frac {x'(t)}{\sqrt {x'(t)^{2}+y'(t)^{2}}}}\int _{a}^{t}{\sqrt {x'(w)^{2}+y'(w)^{2}}}\,dw\\Y(t)&=y(t)-{\frac {y'(t)}{\sqrt {x'(t)^{2}+y'(t)^{2}}}}\int _{a}^{t}{\sqrt {x'(w)^{2}+y'(w)^{2}}}\,dw.\end{aligned}}

Proprietà delle involute

Per ricavare le proprietà di una curva regolare è vantaggioso utilizzare la lunghezza dell'arco $s$ come il parametro della curva assegnata, che porta alle seguenti semplificazioni: $|{\vec {c}}'(s)|=1\;$ e ${\vec {c}}''(s)=\kappa (s){\vec {n}}(s)$ , con $\kappa$ la curvatura e ${\vec {n}}$ l'unità normale. Si ottiene per l'involuta:

{\vec {C}}_{a}(s)={\vec {c}}(s)-{\vec {c}}'(s)(s-a)

e

{\vec {C}}_{a}'(s)=-{\vec {c}}''(s)(s-a)=-\kappa (s){\vec {n}}(s)(s-a)

oltre al seguente risultato:

nel punto ${\vec {C}}_{a}(a)$ l'involuta non è regolare (perché $|{\vec {C}}_{a}'(a)|=0$ ).

Da ${\vec {C}}_{a}'(s)\cdot {\vec {c}}'(s)=0$ segue che:

La normale dell'involuta al punto ${\vec {C}}_{a}(s)$ è la tangente della curva data nel punto ${\vec {c}}(s)$ .
Le involute sono curve parallele, poiché ${\vec {C}}_{a}(s)={\vec {C}}_{0}(s)+a{\vec {c}}'(s)$ e poiché ${\vec {c}}'(s)$ è il vettore unitario normale a ${\vec {C}}_{0}(s)$ .

Esempi

Involuta di una circonferenza

Per una circonferenza con rappresentazione parametrica $(r\cos(t),r\sin(t))$ , si ha ${\vec {c}}'(t)=(-r\sin t,r\cos t)$ . Quindi $|{\vec {c}}'(t)|=r$ e la lunghezza del percorso è $r(t-a)$ .

Calcolando l'equazione sopra indicata dell'involuta, si ottiene

{\begin{aligned}X(t)&=r(\cos t+(t-a)\sin t)\\Y(t)&=r(\sin t-(t-a)\cos t)\end{aligned}}

per l'equazione parametrica dell'involuta della circonferenza.

La lunghezza dell'arco per $a=0$ e $0\leq t\leq t_{2}$ dell'involuta è

L={\frac {r}{2}}t_{2}^{2}.

Involute di una parabola semicubica

L'equazione parametrica ${\vec {c}}(t)=({\frac {t^{3}}{3}},{\frac {t^{2}}{2}})$ , l'equazione dell'involuta è quindi

{\begin{aligned}X(t)&=-{\frac {t}{3}}\\Y(t)&={\frac {t^{2}}{6}}-{\frac {1}{3}}.\end{aligned}}

Eliminando $t$ si ottiene $Y={\frac {3}{2}}X^{2}-{\frac {1}{3}},$ dimostrando che questa involuta è una parabola.

Le altre involute sono quindi curve parallele di una parabola e non sono parabole, poiché sono curve di grado sei.

L'involuta (rossa) di una catenaria (blu) è una trattrice.

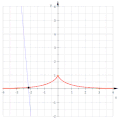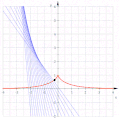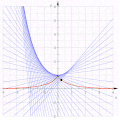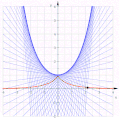
Involute di una catenaria

Per la catenaria $(t,\cosh t)$ , il vettore tangente è ${\vec {c}}'(t)=(1,\sinh t)$ , e come $1+\sinh ^{2}t=\cosh ^{2}t,$ la sua lunghezza è $|{\vec {c}}'(t)|=\cosh t$ . Quindi la lunghezza dell'arco dal punto (0, 1) è $\textstyle \int _{0}^{t}\cosh w\,dw=\sinh t.$

Quindi l'involuta a partire da $(0,1)$ è parametrizzata da

(t-\tanh t,1/\cosh t),

ed è quindi una trattrice.

Le altre involute non sono trattrici, poiché sono curve parallele di una trattrice.

Involute di una cicloide

La rappresentazione parametrica ${\vec {c}}(t)=(t-\sin t,1-\cos t)$ descrive una cicloide. A partire dal ${\vec {c}}'(t)=(1-\cos t,\sin t)$ , si ottiene (dopo aver usato alcune formule trigonometriche)

|{\vec {c}}'(t)|=2\sin {\frac {t}{2}},

e

\int _{\pi }^{t}2\sin {\frac {w}{2}}\,dw=-4\cos {\frac {t}{2}}.

Quindi le equazioni dell'involuta corrispondente sono

{\begin{aligned}X(t)&=-{\frac {t}{3}}\\Y(t)&={\frac {t^{2}}{6}}-{\frac {1}{3}}.\end{aligned}}

che descrivono la cicloide rossa spostata del diagramma. Quindi le involute della cicloide $(t-\sin t,1-\cos t)$ sono curve parallele della cicloide

(t-\tanh t,1/\cosh t).

Le curve parallele di una cicloide non sono cicloidi.

Involute ed evolute

L'evoluta di una data curva $c_{0}$ è costituita dai centri di curvatura di $c_{0}$ . Tra involute ed evolute vale la seguente relazione:^[3]^[4]

Una curva è l'evoluta di una qualsiasi delle sue evolventi (involute).

Involuta ed evoluta
Una trattrice (in rosso) come un'involuta di una catenaria
L'evoluta di una trattrice è una catenaria

Applicazioni

L'involuta ha alcune proprietà che lo rendono estremamente importante per l'industria degli ingranaggi: se due ingranaggi a maglie incrociate hanno denti con la forma del profilo di involute (piuttosto che, ad esempio, una forma triangolare tradizionale), formano un sistema di ingranaggi a spirale. Le loro velocità di rotazione relative sono costanti mentre i denti sono impegnati. Gli ingranaggi inoltre entrano sempre in contatto lungo un'unica linea di forza costante. Con denti di altre forme, le velocità e le forze relative aumentano e diminuiscono quando i denti successivi si impegnano, provocando vibrazioni, rumore e usura eccessiva. Per questo motivo, quasi tutti i moderni ingranaggi hanno la forma a evolvente.^[5]

Note

^ J.W. Rutter, Geometry of Curves, CRC Press, 2000, pp. 204, ISBN 9781584881667.
^ John McCleary, Geometry from a Differentiable Viewpoint, Cambridge University Press, 2013, pp. 89, ISBN 9780521116077.
^ K. Burg, H. Haf, F. Wille, A. Meister: Vektoranalysis: Höhere Mathematik für Ingenieure, Naturwissenschaftler und ..., Springer-Verlag, 2012,ISBN 3834883468, S. 30.
^ R. Courant:Vorlesungen über Differential- und Integralrechnung, 1. Band, Springer-Verlag, 1955, S. 267.
^ V. G. A. Goss (2013) "Application of analytical geometry to the shape of gear teeth", Resonance 18(9): 817 to 31 Springerlink (subscription required).

Voci correlate

Altri progetti

Wikimedia Commons contiene immagini o altri file su evolvente

Collegamenti esterni

Involuta in MathWorld

[1] J.W. Rutter, Geometry of Curves, CRC Press, 2000, pp. 204, ISBN 9781584881667.

[2] John McCleary, Geometry from a Differentiable Viewpoint, Cambridge University Press, 2013, pp. 89, ISBN 9780521116077.

[3] K. Burg, H. Haf, F. Wille, A. Meister: Vektoranalysis: Höhere Mathematik für Ingenieure, Naturwissenschaftler und ..., Springer-Verlag, 2012,ISBN 3834883468, S. 30.

[4] R. Courant:Vorlesungen über Differential- und Integralrechnung, 1. Band, Springer-Verlag, 1955, S. 267.

[5] V. G. A. Goss (2013) "Application of analytical geometry to the shape of gear teeth", Resonance 18(9): 817 to 31 Springerlink (subscription required).

[1]

[2]

[3]

[4]

[5]

Involuta

Indice