Incidenza (geometria)

In matematica due insiemi sono incidenti quando hanno almeno un elemento in comune, ovvero quando la loro intersezione non è vuota.

In geometria descrittiva l'incidenza indica anche l'intersezione di due insiemi nel piano o nello spazio euclideo, considerando anche i punti impropri.

Ad esempio, il punto d'incidenza di due rette distinte nel piano è il loro punto d'intersezione; similmente nello spazio si hanno il punto d'incidenza di un piano e di una retta non contenuta in esso, oppure la retta d'incidenza di due piani distinti.

La sezione di una figura piana rispetto ad una retta o di una figura solida rispetto ad un piano sono casi particolari di incidenza.

Esempi d'incidenza nel piano

Punto d'intersezione tra due rette complanari

Esso indica un punto Q comune a due rette r s appartenenti ad un stesso piano α. Nel caso in cui r ed s sono tra loro inclinati si ha che Q è un punto proprio, altrimenti si ha che Q è un punto improprio, cioè, quando tali rette r s sono tra loro paralleli.

La complanarità tra due assegnate rette r s, disposte nello spazio, può essere verficata, solo quando si eseguono almeno due proiezioni, sia centrali sia paralleli, di tali rette r s. Per esempio, nel metodo di Monge (che fa parte della categoria delle proiezioni parallele), la complanaritò può essere verficata quando le proiezioni ortogonali del punto d'intersezione tra le dette rette r ed s appartiene ad una stessa retta di richiamo.

Esempi d'incidenza nello spazio

Retta d'intersezione tra due piani

La retta d'intersezione tra due piani alpha e beta può essere individuata determinando due punti P Q comuni a tali piani. Nel caso in cui tali piani alpha e beta sono tra loro paralleli si ha che tali punti P Q sono entrambi impropri.

Applicazione

La determinazione di una retta u comune a due assegnati piani alpha e beta, consiste nel eseguire, in ordine, le seguenti operazioni:

• determinare un primo punto P comune ad alpha e beta:
  • si assume un piano ausiliario gamma. Tra gli infiniti piani ausiliari che si possono assumere, spesso per la facilita d'uso, si sceglie quello che ha giacitura verticale.
  • si determinano r s, rispettivamente: come rette d'intersezione tra il piano ausiliario gamma con alpha e beta.
  • infine si individua il punto cercato P, come intersezione tra le rette determinate r ed s.

• si ripetono le operazioni precedenti per determinare un secondo punto Q, anche esso comune ai piani assegnati alpha e beta. A tale fine e per facilitare tali operazioni, è preferibile assumere un secondo piano ausiliario delta che sia parallelo a gamma. in questo modo delta seziona i piani alpha e beta secondo due rette paralleli ad r s.

Punto d'intersezione di una retta con un piano

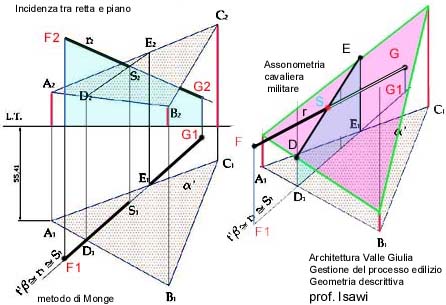
Dati una retta e ed un piano alpha non passante per r (vedi figura). Il punto d'intersezione S tra gli elementi dati, il quale può essere improprio quando r risulta parallela ad alpha, altrimento proprio, quando r è inclinata rispetto ad alpha. Per determinare tale punto S, si procede come di seguito:

• si fa passare per r un piano ausiliario beta.
• si determina una retta s come intersezione tra i piani α e β.
• si individua, in ultimo, il punto cercato S come intersezione tra la rette r s.

Si tiene presente che nel caso in cui risulta che tali rette r s sono tra loro paralleli, significa che r è parallela al piano α.

Incidenza di una retta r con una superficie proiettiva

Incidenza di r con un cilindro

dati le P.O. di un cilindro K e di una retta r, in cui è stabilito che K ha base circolare appartenente al primo piano di proiezione (pigreco)1 ed asse inclinato rispetto a tale piano, si vuole determinare eventuali punti d'incidenza di r con K.

Il concetto d'intersezione di una retta r con cilindro K si basa sul fatto che i piani che passano per il vertice di K ( cioè // al suo asse) lo sezionano seconda due generatrici (in questo caso sono due rette), e poiché un punto improprio ( vertice del cilindro) e la retta data r individuano un solo piano alfa, per cui, è sufficiente individuare tale piano alpha per risolvere il problema in questione. Per inciso:

• la prima traccia di alfa si individua unendo la prima traccia di r con la prima traccia di un'altra retta s complanare ad r ed // all'asse del cilindro K.
• Dove la prima traccia di alfa interseca la base inferiore di k, passano le due generatrici, m n, d'intersezione tra alpha e K.
• In ultimo, i punti d'incidenza di r con K, si individuano come intersezione delle dette generatrici m n con r.

Nota importante: Con procedimento analogo, come sopra, è possibile determinare l'intersezione di un retta con qualsiasi tipo di superficie proiettiva, come le superfici coniche, le piramidi, i prismi.

Voci correlate

• Angolo d'incidenza
• Insieme
• Intersezione
• Punto improprio
• Spazio euclideo
• Sezione (geometria)

Portale Matematica: accedi alle voci di Wikipedia che trattano di matematica