Algoritmo di Borůvka

Algoritmo di Borůvka
Animazione dell'algoritmo di Boruvka
Classe	Albero ricoprente minimo
Struttura dati	Grafo
Caso peggiore temporalmente	$O(|E|\log |V|)$

L'algoritmo di Borůvka è un algoritmo per la ricerca di un albero ricoprente minimo in un grafo in cui il peso di ciascuna coppia di archi sia distinto. Se due archi hanno peso uguale, è sufficiente modificare anche minimamente il peso di uno dei due archi per rendere valido l'algoritmo.

L'algoritmo venne pubblicato nel 1926 da Otakar Borůvka come metodo di costruzione di un'efficiente rete elettrica per la Moravia (Repubblica Ceca). L'algoritmo fu riscoperto da Choquet nel 1938; successivamente da Florek, Łukasiewicz, Perkal, Steinhaus, e Zubrzycki nel 1951; e ancora da Sollin probabilmente all'inizio degli anni '60. Dato che Sollin fu l'unico informatico occidentale in tale lista, questo algoritmo è spesso chiamato algoritmo di Sollin, specialmente nella letteratura del computing parallelo.

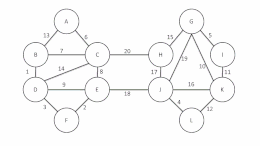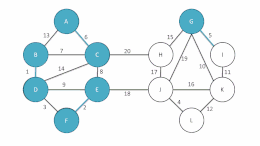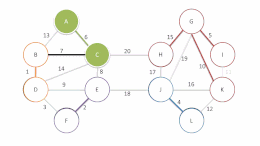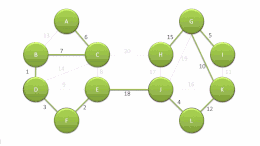
Algoritmo

L'algoritmo comincia esaminando ciascun vertice e aggiungendo l'arco di costo minore da quel vertice ad un altro nel grafo, senza tenere conto di archi già aggiunti, e continua unendo questi raggruppamenti in modo simile finché un albero ricoprente tutti i vertici si completa. Lo pseudocodice per l'algoritmo è:

• Inizia con un grafo connesso G contenente archi di peso diverso, e un insieme di archi vuoto, T
• Finché i vertici di G connessi da T sono disgiunti:
  • Inizia con un insieme vuoto di archi E
  • Per ciascun componente:
    • Inizia con un insieme di archi vuoto S
    • Per ciascun vertice nel componente:
      • Aggiungi l'arco di costo minore dal vertice nel componente verso un altro vertice in un componente disgiunto a S
    • Aggiungi l'arco di costo minore da S a E
  • Aggiungi l'insieme di archi risultante da E a T.
• L'insieme di archi risultanti T è il minimum spanning tree di G

L'algoritmo di Borůvka si dimostra avere una complessità computazionale O(E log V), dove E è il numero di archi, e V è il numero di vertici in G.

Altri algoritmi utili alla causa sono l'algoritmo di Prim (in realtà scoperto da Vojtěch Jarník) e l'algoritmo di Kruskal. Algoritmi più veloci si ottengono combinando l'algoritmo di Prim e quello di Borůvka. Una versione randomizzata più veloce realizzata da Karger, Klein, e Tarjan lavora in tempi asintotici lineari nel numero di archi. Il più conosciuto algoritmo di calcolo dell'albero ricoprente minimo realizzato da Bernard Chazelle si basa su Borůvka e lavora in tempo O(E α(V)), dove α è l'inverso della Funzione di Ackermann.

Bibliografia

• Robert E. Tarjan, Data structures and network algorithms, Philadelphia, Society for Industrial and Applied Mathematics, 1983, ISBN 978-0-89871-187-5, OCLC 10120539.

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file su algoritmo di Borůvka