Generatore lineare congruenziale

La disposizione dei punti generati dal Generatore Lineare ran0

In matematica il generatore lineare congruenziale (LCG dall'inglese Linear Congruential Generator) è un algoritmo per la generazione di numeri pseudo-casuali vecchio e molto conosciuto. La teoria sulla quale poggia è semplice da capire e da implementare; inoltre ha il vantaggio di essere computazionalmente leggero.

Il generatore è definito ricorsivamente:

$X_{n+1}=\left(aX_{n}+c\right)\ {\bmod {\ }}m$

dove $X_{n}$ è un valore della successione dei numeri pseudocasuali e

$m,\,0<m$ — il "modulo"

$a,\,0<a<m$ — il "moltiplicatore"

$c,\,0\leq c<m$ — l'"incremento" (nel caso speciale in cui $c=0$ si parla di generatore Park-Miller RNG o moltiplicativo)

$X_{0},\,0\leq X_{0}<m$ — il "seme" o il "valore iniziale"

Il periodo di un LCG è al più m, e per alcune scelte di a può essere molto più piccolo. Il LCG ha un periodo pieno se e solo se:

1. $c$ e $m$ sono coprimi
2. $a-1$ è divisibile per tutti i fattori primi di $m$,
3. $a-1$ è un multiplo di 4 se $m$ è un multiplo di 4.

Nonostante gli LCG siano generalmente in grado di produrre numeri pseudocasuali decenti, la loro qualità è molto sensibile alla scelta dei coefficienti c, m ed a.

Storicamente, scelte sbagliate hanno portato a implementazioni inefficienti di LCG. Un esempio significativo è RANDU che è stato usato largamente nei primi anni '70 e ha portato a dei risultati che attualmente sono messi in dubbio a causa dell'uso di un LCG di scarsa qualità.

Se un generatore congruenziale lineare è inizializzato con un carattere e iterato, il risultato è un semplice cifrario classico chiamato cifrario affine; questo cifrario è facilmente forzabile con un'analisi frequentista standard.

Esempi

Generatori di base

Grafico del Generatore lineare definito a lato. Si nota come la funzione è periodica di periodo 4

Un esempio di generatore di base può essere dato da

$a=3$

$c=1$

$m=5$

$X_{0}=1$

Ossia:

$X_{i+1}=3\cdot X_{i}+1{\pmod {5}}$

La sequenza generata è:

$X_{1}=3\cdot X_{0}+1{\pmod {5}}=4$

$X_{2}=3\cdot X_{1}+1{\pmod {5}}=3$

$X_{3}=3\cdot X_{2}+1{\pmod {5}}=0$

$X_{4}=3\cdot X_{3}+1{\pmod {5}}=1$

$X_{5}=3\cdot X_{4}+1{\pmod {5}}=4$

$X_{6}=3\cdot X_{5}+1{\pmod {5}}=3$

Il periodo è uguale a quattro.

Esempi di utilizzo

Il generatore congruenziale lineare più efficiente ha m uguale a una potenza di 2, spesso m = 2³² o m = 2⁶⁴ perché questo consente di calcolare l'operazione modulo semplicemente troncando i 32 o i 64 bit meno significativi. La seguente tabella lista i parametri degli LCG di uso comune, inclusa le funzioni rand() di alcuni compilatori.

Source	m	a	c	output bits of seed in rand() / Random(L)
Numerical Recipes	232	1664525	1013904223
Borland C/C++	232	22695477	1	bits 30..16 in rand(), 30..0 in lrand()
glibc (usato da GCC)	232	1103515245	12345	bits 30..0
ANSI C: Watcom, Digital Mars, CodeWarrior, IBM VisualAge C/C++	232	1103515245	12345	bits 30..16
Borland Delphi, Virtual Pascal	232	134775813	1	bits 63..32 of (seed * L)
Microsoft Visual/Quick C/C++	232	214013	2531011	bits 30..16
Apple CarbonLib	231 − 1	16807	0	see Park–Miller RNG
MMIX di Donald Knuth	264	6364136223846793005	1442695040888963407
VAX's MTH$RANDOM, old versions of glibc	232	69069	1
Random class nelle API di Java	248	25214903917	11	bits 48...17

Come mostrato sopra, LCG non usa sempre tutti i bit che produce. L'implementazione Java produce 48 bit ad ogni iterazione ma sono ritornati come risultato solo i 32 bit più significativi. Questo poiché i bit più significativi hanno un periodo più lungo. Gli algoritmi che usano questa soluzione sono migliori.

Vantaggi e svantaggi

I generatori congruenziali lineari richiedono una memoria minima (tipicamente 32 o 64 bit) per memorizzare lo stato.

Iperpiani di un generatore congruenziale lineare in tre dimensioni

Gli LCG non dovrebbero essere usati in applicazioni dove è critico l'utilizzo dell'alta casualità.

Per esempio, non sono adatti per simulazioni Monte Carlo poiché hanno una correlazione tra di loro. Non devono essere usati in crittografia.

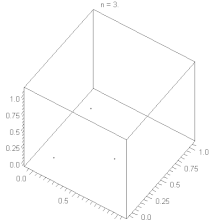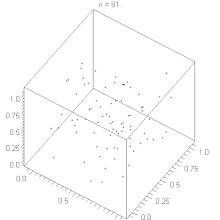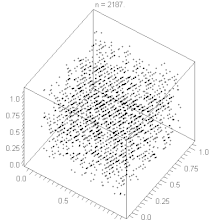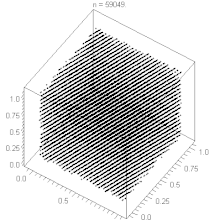
Inoltre questi algoritmi tendono ad avere alcuni difetti. Per esempio, se un LCG è usato per scegliere i punti in uno spazio n-dimensionale, i punti giacciono su iperpiani al massimo m^1/n-dimensionali (teorema di Marsaglia). Questo è dovuto ad una correlazione tra valori successivi della successione.

Un altro problema è che negli LCG i bit meno significativi della sequenza generata hanno un periodo più corto di quello della sequenza se m è posto ad essere una potenza di 2. In generale, la n-esima cifra meno significativa nella base b della sequenza prodotta, dove $b^{k}=m$ per qualche intero k, si ripete con un periodo al più $b^{n}$.

Nonostante ciò, gli LGC possono essere una buona scelta in alcuni contesti, come per esempio nei sistemi embedded, dove la memoria disponibile è spesso molto limitata; anche nel caso di un videogioco, prendere un piccolo numero dei bit più significativi potrebbe essere sufficiente. I bit meno significativi di un LCG dove m è una potenza di 2 non dovrebbero mai essere usati.

Confronto con altri metodi

Se è necessario avere numeri pseudocasuali di qualità e una certa memoria è disponibile (~ 2 kilobytes), allora l'algoritmo Mersenne Twister fornisce un periodo molto maggiore (2^19937-1)

Voci correlate

• Numeri pseudo-casuali
• Generatore di Fibonacci ritardato
• Generatore hardware di numeri casuali
• Mersenne Twister
• Funzione periodica

Collegamenti esterni

• Generazione di numeri casuali (PDF) , su www-tlc.deis.unibo.it.
• Generatore di numeri casuali (Regione Emilia-Romagna), su regione.emilia-romagna.it.