Funzione di correlazione (meccanica statistica)

In meccanica statistica, la funzione di correlazione è una misura dell'ordine in un sistema, caratterizzato da una funzione di correlazione matematica. Le funzioni di correlazione descrivono come sono correlate variabili microscopiche, come spin e densità, in posizioni diverse. Più specificamente, le funzioni di correlazione quantificano come le variabili microscopiche co-variano tra loro in media nello spazio e nel tempo. Un classico esempio di tali correlazioni spaziali lo si trova nei modelli dei materiali ferromagnetici e antiferromagnetici, dove gli spin preferiscono allinearsi rispettivamente in maniera parallela o antiparallela con i loro vicini più prossimi. La correlazione spaziale tra gli spin in tali materiali è mostrata nella figura a destra.

Definizioni

La definizione più comune di una funzione di correlazione è la media rispetto all'ensemble canonico (termica) del prodotto scalare di due variabili casuali, $s_{1}$ e $s_{2}$ , nelle posizioni $R$ e $R+r$ e ai tempi $t$ e $t+\tau$ :

$C(r,\tau )=\langle \mathbf {s_{1}} (R,t)\cdot \mathbf {s_{2}} (R+r,t+\tau )\rangle \ -\langle \mathbf {s_{1}} (R,t)\rangle \langle \mathbf {s_{2}} (R+r,t+\tau )\rangle \,.$

Dove le parentesi $\langle ...\rangle$ indicano la suddetta media termica. È una questione di convenzione il fatto di sottrarre il prodotto medio non correlato di $s_{1}$ e $s_{2}$ , $\langle \mathbf {s_{1}} (R,t)\rangle \langle \mathbf {s_{2}} (R+r,t+\tau )\rangle$ dal prodotto correlato, $\langle \mathbf {s_{1}} (R,t)\cdot \mathbf {s_{2}} (R+r,t+\tau )\rangle$ , con convenzioni differenti in ambiti diversi. Gli usi più comuni delle funzioni di correlazione si hanno quando $s_{1}$ e $s_{2}$ descrivono la stessa variabile, come il caso della funzione di correlazione spin-spin, o della funzione di correlazione posizione-posizione delle particelle in un liquido elementare o in un solido (spesso chiamata funzione di distribuzione radiale o funzione di correlazione di coppia). Le funzioni di correlazione tra due valori della stessa variabile casuale sono funzioni di autocorrelazione. Tuttavia, in meccanica statistica, non tutte le funzioni di correlazione sono funzioni di autocorrelazione. Ad esempio, nelle fasi condensate multicomponente, la funzione di correlazione di coppia tra elementi diversi assume spesso importanza. Tali funzioni di correlazione di coppie di elementi misti sono un esempio di funzioni di correlazione incrociata, dove le variabili casuali $s_{1}$ e $s_{2}$ rappresentano le variazioni medie di densità in funzione della posizione per due elementi distinti.

Funzione di correlazione (spaziale) di equilibrio a tempo fissato

Spesso si è interessati esclusivamente all'influenza spaziale di una data variabile casuale, per esempio la direzione di una rotazione, rispetto al suo ambiente locale, senza considerare i tempi $\tau$ successivi. In questo caso, si trascura l'evoluzione temporale del sistema, per cui la definizione di cui sopra viene riscritta con $\tau =0$ . Questa si definisce funzione di correlazione a tempo uguale, $C(r,0)$ :

$C(r,0)=\langle \mathbf {s_{1}} (R,t)\cdot \mathbf {s_{2}} (R+r,t)\rangle \ -\langle \mathbf {s_{1}} (R,t)\rangle \langle \mathbf {s_{2}} (R+r,t)\rangle \,.$

Spesso si omette il tempo di riferimento, $t$ , e il raggio di riferimento, $R$ , assumendo l'equilibrio (e quindi l'invarianza temporale del sistema) e mediando su tutte le posizioni del campione, ottenendo:

$C(r)=\langle \mathbf {s_{1}} (0)\cdot \mathbf {s_{2}} (r)\rangle \ -\langle \mathbf {s_{1}} (0)\rangle \langle \mathbf {s_{2}} (r)\rangle \,.$

dove, ancora, la scelta di sottrarre le variabili non correlate dipende dall'ambito. La funzione di distribuzione radiale è un esempio di una funzione di correlazione a tempo uguale in cui il valore non correlato generalmente non viene sottratto.

Funzioni di correlazione (temporale) di equilibrio a posizione fissata

Si potrebbe anche essere interessati all'evoluzione temporale delle variabili microscopiche. In altre parole, a come il valore di una variabile microscopica in una data posizione e istante, $R$ e $t$ , influenza il valore della stessa variabile microscopica in un secondo tempo, $t+\tau$ (e di solito nella stessa posizione). Tali correlazioni temporali sono quantificate tramite funzioni di correlazione a posizione fissata, $C(0,\tau )$ . Sono definite in modo analogo alle precedenti funzioni di correlazione a tempo uguale, trascurando le dipendenze spaziali ponendo $r=0$ , ottenendo:

$C(0,\tau )=\langle \mathbf {s_{1}} (R,t)\cdot \mathbf {s_{2}} (R,t+\tau )\rangle \ -\langle \mathbf {s_{1}} (R,t)\rangle \langle \mathbf {s_{2}} (R,t+\tau )\rangle \,.$

Assumendo l'equilibrio (e quindi l'invarianza temporale del sistema) e calcolando la media su tutti i siti nel campione, si ottiene un'espressione più semplice per la funzione di correlazione di posizione uguale analoga a quella della funzione di correlazione a tempo fissato:

$C(\tau )=\langle \mathbf {s_{1}} (0)\cdot \mathbf {s_{2}} (\tau )\rangle \ -\langle \mathbf {s_{1}} (0)\rangle \langle \mathbf {s_{2}} (\tau )\rangle \,.$

L'assunzione di cui sopra può sembrare a prima vista non intuitiva: come può un insieme che è invariante rispetto al tempo, avere una funzione di correlazione temporale non uniforme? Le correlazioni temporali rimangono delle quantità non banali nei sistemi all'equilibrio termodinamico perché un sistema macroscopico invariante rispetto al tempo può ancora avere una dinamica temporale microscopica non banale. Un esempio è quello della diffusione. Un sistema monofase all'equilibrio ha una composizione omogenea da un punto di vista macroscopico. Tuttavia, se si osserva il moto microscopico di ciascun atomo, si verificano costantemente fluttuazioni nella composizione a causa delle passeggiate quasi casuali compiute dai singoli atomi. La meccanica statistica consente di estrarre informazioni importanti a partire dal comportamento temporale di tali fluttuazioni dei sistemi di equilibrio (ad esempio con le formule di Green-Kubo).

Generalizzazione lontano dall'equilibrio

Tutte le funzioni di correlazione di cui sopra sono state definite nel contesto della meccanica statistica di equilibrio. Tuttavia, è possibile definire funzioni di correlazione per sistemi lontani dall'equilibrio. Considerando la definizione generale di $C(r,\tau )$ , è chiaro che si possono considerare le variabili casuali utilizzate in queste funzioni di correlazione, come la posizione degli atomi o gli spin, lontano dall'equilibrio. In quanto tale, il loro prodotto scalare rimane ben definito anche lontano dall'equilibrio. L'operazione che invece non è più ben definita fuori dall'equilibrio è la media sull'insieme canonico (definito appunto all'equilibrio). Questo processo di media per il sistema di non equilibrio viene in genere sostituito dalla media del prodotto scalare sull'intero dominio. Questo è tipico degli esperimenti di scattering e delle simulazioni al computer ed è spesso usato per misurare le funzioni di distribuzione radiale nei sistemi vetrosi.

Misurare le funzioni di correlazione

Le funzioni di correlazione sono in genere misurate con esperimenti di scattering. Ad esempio, gli esperimenti di diffrazione dei raggi X misurano direttamente le correlazioni elettrone-elettrone a tempo fissato.^[1] Dalla conoscenza dei fattori di struttura elementare, si possono anche misurare le funzioni di correlazione delle coppie elementari. Vedere funzione di distribuzione radiale per ulteriori informazioni. Le funzioni di correlazione spin-spin a tempo fissato sono invece misurate con lo scattering di neutroni anziché con lo scattering di raggi X. Lo scattering di neutroni può anche fornire informazioni sulle correlazioni di coppia. Per i sistemi composti da particelle più grandi di circa un micron, la microscopia ottica può essere utilizzata per misurare sia le funzioni di correlazione a tempo fissato che a posizione fissata. La microscopia ottica è quindi molto impiegata per lo studio delle sospensioni colloidali, specialmente in due dimensioni.

Evoluzione temporale delle funzioni di correlazione

Nel 1931, Lars Onsager propose che la regressione delle fluttuazioni termiche microscopiche all'equilibrio seguisse la legge macroscopica del rilassamento di piccoli disturbi di non equilibrio.^[2] Questa è nota come ipotesi di regressione di Onsager. Poiché i valori delle variabili microscopiche dovrebbero non essere correlati se esse sono separate da scale temporali $\tau$ sufficientemente lunghe (oltre quanto ci si aspetterebbe dalla condizione di equilibrio termodinamico), l'evoluzione nel tempo di una funzione di correlazione può essere vista, da un punto di vista fisico, come il fatto che il sistema gradualmente "dimentica" le sue condizioni iniziali specificate da qualche variabile microscopica. Esiste infatti una connessione intuitiva tra l'evoluzione temporale delle funzioni di correlazione e l'evoluzione temporale dei sistemi macroscopici: in media, la funzione di correlazione evolve nel tempo allo stesso modo di un sistema fisico costruito in modo da avere come condizioni iniziali quelle specificate dal valore iniziale della funzione di correlazione.^[1]

Le fluttuazioni del sistema all'equilibrio possono essere collegate alle sue risposte a perturbazioni esterne tramite il teorema di fluttuazione-dissipazione.

Connessione tra transizioni di fase e funzioni di correlazione

Le transizioni di fase continue, come le transizioni ordine-disordine nelle leghe metalliche e le transizioni ferromagnetismo-paramagnetismo, implicano una transizione da uno stato ordinato a uno disordinato, al crescere della temperatura. In termini di funzioni di correlazione, la funzione di correlazione a tempo fissato è diversa da zero per tutti i punti del reticolo al di sotto della temperatura critica, mentre al di sopra della temperatura critica non è trascurabile solo a brevi distanze. Poiché la transizione di fase è continua, la lunghezza $\xi$ entro la quale le variabili microscopiche sono correlate deve passare in modo continuo dall'essere infinita a finita quando il materiale viene portato da sotto a sopra la temperatura critica. Ciò dà luogo a una dipendenza a legge di potenza della funzione di correlazione rispetto alla distanza, quando il sistema si trova nel punto critico. Ciò è mostrato nella figura a destra nel caso di un materiale ferromagnetico, con i dettagli quantitativi riportati nella successiva sezione riguardante il magnetismo.

Applicazioni

Magnetismo

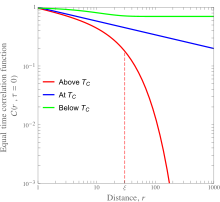
In un modello di spin, la funzione di correlazione a tempo fissato viene comunemente studiata. Essa corrisponde alla media rispetto all'insieme canonico (termica) del prodotto scalare degli spin in due punti del reticolo, rispetto a tutti i possibili ordinamenti:

$C(r)=\langle \mathbf {s} (R)\cdot \mathbf {s} (R+r)\rangle \ -\langle \mathbf {s} (R)\rangle \langle \mathbf {s} (R+r)\rangle \,.$

Qui le parentesi denotano la suddetta media termica. La figura a sinistra mostra gli andamenti di tale funzione per un materiale ferromagnetico al di sotto, esattamente alla, e al di sopra della sua temperatura di Curie.

Anche in una fase magneticamente disordinata, gli spin in siti diversi del reticolo sono correlati, cioè se la distanza $r$ è molto piccola (rispetto ad una qualche scala di lunghezza $\xi$ ), l'interazione tra gli spin farà sì che siano correlati. L'allineamento che deriverebbe naturalmente dall'interazione tra gli spin viene distrutto dagli effetti termici. Ad alte temperature si osservano un decadimento esponenziale della funzione di correlazione all'aumentare della distanza, con un comportamento asintotico del tipo:

C(r)\approx {\frac {1}{r^{\vartheta }}}\exp {\left(-{\frac {r}{\xi }}\right)}\,,

dove $r$ è la distanza tra gli spin, $d$ è la dimensionalità del sistema, e $\vartheta$ è un esponente, il cui valore dipende dal fatto che il sistema si trovi nella fase disordinata (cioè al di sopra del punto critico), o nella fase ordinata (cioè al di sotto del punto critico). Ad alte temperature, la correlazione decade esponenzialmente a zero rispetto alla distanza tra gli spin. Lo stesso decadimento esponenziale in funzione della distanza radiale lo si osserva anche al di sotto di $T_{c}$ , ma anziché tendere a zero tende alla magnetizzazione media $\langle M^{2}\rangle$ . Proprio nel punto critico si vede un comportamento algebrico del tipo:

C(r)\approx {\frac {1}{r^{(d-2+\eta )}}}\,,

dove $\eta$ è un esponente critico, che non ha alcuna relazione banale con l'esponente non critico $\vartheta$ introdotto sopra. Ad esempio, la soluzione esatta del modello di Ising in due dimensioni (con interazioni ferromagnetiche a corto raggio) fornisce come al punto critico $\eta ={\frac {1}{4}}$ , ma al di sopra di $T_{c}$ si ha $\vartheta ={\frac {1}{2}}$ , mentre al di sotto di $T_{c}$ $\vartheta =2$ .^[3]^[4]

Quando la temperatura si abbassa, il disordine termico diminuisce e in una transizione di fase continua la lunghezza di correlazione $\xi$ diverge, dato che la lunghezza di correlazione deve passare in modo continuo da un valore finito al di sopra del punto critico, a uno infinito al di sotto:

\xi \propto |T-T_{c}|^{-\nu }\,,

dove $\nu$ è un altro esponente critico.

Questa legge di potenza della lunghezza di correlazione è responsabile dell'invarianza di scala, osservata in queste transizioni. Tutti gli esponenti citati sono indipendenti dalla temperatura. Sono infatti universali, cioè sono gli stessi in un'ampia varietà di sistemi.

Funzioni di distribuzione radiale

Un altro tipo di funzione di correlazione comunemente usato è la funzione di distribuzione radiale, che si vede spesso in meccanica statistica e in meccanica dei fluidi. La funzione di correlazione può essere calcolata in modelli esattamente risolvibili (gas di Bose unidimensionale, catene di spin, modello di Hubbard) usando il metodo di scattering inverso quantistico e l'ansatz di Bethe. In un modello XY isotropo, le correlazioni temporali e di temperatura sono state stimate da Its, Korepin, Izergin e Slavnov.^[5]

Funzioni di correlazione di ordine superiore

Le funzioni di correlazione di ordine superiore coinvolgono un numero maggiore di punti di riferimento e sono definite attraverso una generalizzazione della definizione precedente di funzione di correlazione, prendendo il valore atteso del prodotto di più di due variabili casuali:

C_{i_{1}i_{2}\cdots i_{n}}(s_{1},s_{2},\cdots ,s_{n})=\langle X_{i_{1}}(s_{1})X_{i_{2}}(s_{2})\cdots X_{i_{n}}(s_{n})\rangle .

Tali funzioni di correlazione di ordine superiore sono però relativamente difficili da misurare o da interpretare. Per esempio, per poter misurare l'analogo di ordine superiore delle funzioni di distribuzione di coppia, servono sorgenti coerenti di raggi X. Sia gli aspetti teorici di tali analisi,^[6]^[7] che le misure sperimentali di tali funzioni di cross-correlazione dei raggi X,^[8] sono campi di ricerca attiva.

Note

^ ^a ^b James P. Sethna, Chapter 10: Correlations, response, and dissipation, in Statistical Mechanics: Entropy, Order Parameters, and Complexity, Oxford University Press, 2006, ISBN 978-0198566779.
^ Lars Onsager, Reciprocal Relations in Irreversible Processes. I., in Physical Review, vol. 38, n. 405, 1931, pp. 2265–2279, DOI:10.1103/PhysRev.37.405.
^ Barry M. McCoy e Tai Tsun Wu, The Two-Dimensional Ising Model, 31 dicembre 1973, DOI:10.4159/harvard.9780674180758. URL consultato il 27 febbraio 2022.
^ Malte Henkel, Conformal Invariance, Springer Berlin Heidelberg, 1999, pp. 43–62, ISBN 978-3-642-08466-9. URL consultato il 27 febbraio 2022.
^ A. R. Its, A. G. Izergin e V. E. Korepin, Temperature correlations of quantum spins, in Physical Review Letters, vol. 70, n. 11, 15 marzo 1993, pp. 1704–1706, DOI:10.1103/PhysRevLett.70.1704. URL consultato il 27 febbraio 2022.
^ M. Altarelli, R. P. Kurta e I. A. Vartanyants, X-ray cross-correlation analysis and local symmetries of disordered systems: General theory, in Physical Review B, vol. 82, n. 10, 20 settembre 2010, pp. 104207, DOI:10.1103/PhysRevB.82.104207. URL consultato il 27 febbraio 2022.
^ (EN) F. Lehmkühler, G. Grübel e C. Gutt, Detecting orientational order in model systems by X-ray cross-correlation methods, in Journal of Applied Crystallography, vol. 47, n. 4, 1º agosto 2014, pp. 1315–1323, DOI:10.1107/S1600576714012424. URL consultato il 27 febbraio 2022.
^ (EN) Peter Wochner, Christian Gutt, Tina Autenrieth, et al., X-ray cross correlation analysis uncovers hidden local symmetries in disordered matter, in Proceedings of the National Academy of Sciences, vol. 106, n. 28, 14 luglio 2009, pp. 11511–11514, DOI:10.1073/pnas.0905337106. URL consultato il 27 febbraio 2022.

Bibliografia

978-0198566779 James P. Sethna, Chapter 10: Correlations, response, and dissipation, in Statistical Mechanics: Entropy, Order Parameters, and Complexity, Oxford University Press, 2006, ISBN 978-0198566779.
J. M. Yeomans, Statistical Mechanics of Phase Transitions, Oxford Science Publications, 1992, ISBN 978-0-19-851730-6.
978-0-19-851730-6 M. E. Fisher, Renormalization Group in Theory of Critical Behavior, in Reviews of Modern Physics, vol. 46, n. 4, 1974, pp. 597–616, Bibcode:1974RvMP...46..597F, DOI:10.1103/RevModPhys.46.597.
C. Domb, M. S. Green, curato da J. L. Lebowitz, Phase Transitions and Critical Phenomena, vol. 1-20 (1972–2001), Academic Press.

Portale Fisica: accedi alle voci di Wikipedia che trattano di fisica

[Sethna-1] James P. Sethna, Chapter 10: Correlations, response, and dissipation, in Statistical Mechanics: Entropy, Order Parameters, and Complexity, Oxford University Press, 2006, ISBN 978-0198566779.

[2] Lars Onsager, Reciprocal Relations in Irreversible Processes. I., in Physical Review, vol. 38, n. 405, 1931, pp. 2265–2279, DOI:10.1103/PhysRev.37.405.

[3] Barry M. McCoy e Tai Tsun Wu, The Two-Dimensional Ising Model, 31 dicembre 1973, DOI:10.4159/harvard.9780674180758. URL consultato il 27 febbraio 2022.

[4] Malte Henkel, Conformal Invariance, Springer Berlin Heidelberg, 1999, pp. 43–62, ISBN 978-3-642-08466-9. URL consultato il 27 febbraio 2022.

[5] A. R. Its, A. G. Izergin e V. E. Korepin, Temperature correlations of quantum spins, in Physical Review Letters, vol. 70, n. 11, 15 marzo 1993, pp. 1704–1706, DOI:10.1103/PhysRevLett.70.1704. URL consultato il 27 febbraio 2022.

[6] M. Altarelli, R. P. Kurta e I. A. Vartanyants, X-ray cross-correlation analysis and local symmetries of disordered systems: General theory, in Physical Review B, vol. 82, n. 10, 20 settembre 2010, pp. 104207, DOI:10.1103/PhysRevB.82.104207. URL consultato il 27 febbraio 2022.

[7] (EN) F. Lehmkühler, G. Grübel e C. Gutt, Detecting orientational order in model systems by X-ray cross-correlation methods, in Journal of Applied Crystallography, vol. 47, n. 4, 1º agosto 2014, pp. 1315–1323, DOI:10.1107/S1600576714012424. URL consultato il 27 febbraio 2022.

[8] (EN) Peter Wochner, Christian Gutt, Tina Autenrieth, et al., X-ray cross correlation analysis uncovers hidden local symmetries in disordered matter, in Proceedings of the National Academy of Sciences, vol. 106, n. 28, 14 luglio 2009, pp. 11511–11514, DOI:10.1073/pnas.0905337106. URL consultato il 27 febbraio 2022.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

Funzione di correlazione (meccanica statistica)

Indice

Definizioni

Funzione di correlazione (spaziale) di equilibrio a tempo fissato