Rete di Zobel

La rete di Zobel è un tipo di filtro basato sul principio della immagine d'impedenza. Il nome deriva dal suo inventore Otto Julius Zobel del Bell Labs, che pubblicò opere sul tema nel 1923. La caratteristica della rete di Zobel è di avere una impedenza d'ingresso costante indipendentemente dalla funzione di trasferimento. Questo è possibile al costo di implementare più sezioni di filtro e quindi componenti rispetto ad altri filtri. L'impedenza è nominalmente costante e resistiva pura. Per questo motivo le reti di Zobel sono anche dette a resistenza costante. Qualunque impedenza può essere implementata con componenti discreti.

Le reti di Zobel sono largamente utilizzate nelle telecomunicazioni per appiattire e allargare le risposte in frequenza di linee di rame terrestri, aumentando la qualità delle linee telefoniche. L'uso è calato con il passaggio ai sistemi digitali che hanno soppiantato quelli analogici.

Quando utilizzato per cancellare la parte reattiva dell'impedenza di un altoparlante viene chiamato a volte cella di Boucherot. In questo caso, solo metà della rete è implementata con componenti discreti, mentre l’altra parte è formata dal circuito equivalente del trasduttore. È usata anche per la correzione del fattore di potenza nella distribuzione di corrente elettrica, ecco l'associazione al nome Boucherot.

Una configurazione tipica di una rete di Zobel è quella con ponte a T.

Derivazione

Rete di Zobel come ponte bilanciato

La base della rete di Zobel è un ponte bilanciato come mostrato in figura. La condizione di bilanciamento è;

${\frac {Z}{Z_{0}}}={\frac {Z_{0}}{Z'}}$

Se questo è espresso in termini di una normalizzata Z₀ = 1 come convenzionalmente fatto nelle tavole di filtri, la condizione di bilanciamento è semplice;

$Z={\frac {1}{Z'}}$

In altre parole, $\scriptstyle Z'$ è semplicemente l'inverso, o impedenza duale di $\scriptstyle Z$.

L'impedenza del ponte Z_B è attraverso i punti bilanciati e nessun potenziale lo attraversa. Conseguentemente, non vi è corrente che attraversa e il suo valore non fa differenza alla funzione del circuito. Comunque solitamente il suo valore scelto è Z₀ per ragioni che si evincono nella configurazione a T.

Impedenza d'ingresso

L'impedenza d'ingresso è data da

${\frac {1}{Z_{\text{in}}}}={\frac {1}{Z_{0}+Z'}}+{\frac {1}{Z+Z_{0}}}$

Sostituendo la condizione di bilanciamento,

$Z'={\frac {Z_{0}^{2}}{Z}}$

si ottiene

$Z_{\text{in}}=Z_{0}$

La impedenza d'ingresso può essere progettata resistiva pura settando

$Z_{0}=R_{0}\!\,$

L'impedenza d'ingresso sarà quindi reale e indipendente da ω in banda e fuori banda indipendentemente dalla complessità delle sezioni del filtro scelte.

Funzione di trasferimento

Circuito equivalente di rete di Zobel per il calcolo del guadagno

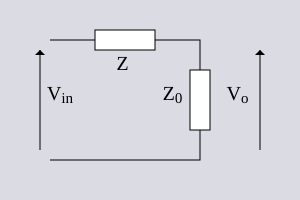
Se Z₀ nella parte sotto a destra del circuito è preso come carico sull'uscita allora la funzione di trasferimento di V_in/V_o può essere calcolata per la sezione. Solo il ramo rhs deve essere considerato per il calcolo. La ragione di questo è da trovare nel fatto che non vi è corrente che scorre attraverso R_B. Nessuna corrente scorre attraverso il ramo lhs verso il carico. Il ramo lhs non può avere effetto sull'uscita. È certamente influenzata l'impedenza d'ingresso (e il voltaggio all'ingresso) ma non la funzione di trasferimento. La funzione di trasferimento è quindi;

$A(\omega )={\frac {Z_{0}}{Z+Z_{0}}}$

Implementazione con ponte a T

Ponte a T di Zobel

L'impedenza del carico è l'impedenza delle sezioni o della linea di trasmissione e può essere omessa dal circuito. Se settiamo;

$Z_{B}=Z_{0}\,\!$

il circuito sulla destra risulta. Questo si riferisce a un ponte a T perché l'impedenza Z è vista dal "ponte" attraverso la sezione a T. Lo scopo di susare Z_B = Z₀ è di rendere simmetrica la sezione del filtro. Questo ha il vantaggio di avere la stessa impedenza, Z₀, sia in ingresso che in uscita.

Tipi di sezione

Unn filtro Zobel può essere implementato come passa basso, passa alto, passa banda o elimina banda. È possibile anche implementare un filtro a risposta piatta di attenuazione.

Attenuatore

Z e Z'  per attenuatore Zobel

Per una sezione che faccia da attenuatore, Z è semplicemente

$Z=R\,\!$

e

$Z'=R'={\frac {R_{0}^{2}}{R}}$

L'attenuazione è data da;

$L=20\log \left({\frac {R}{R_{0}}}+1\right)\,{\text{dB}}$

Passa basso

Z e Z ' per un Zobel passa basso

Per una sezione passa basso, Z è un induttore e Z ' è una capacità;

$Z=i\omega L\!\,$

e

$Z'={\frac {1}{i\omega C'}}$

dove

$C'={\frac {L}{R_{0}^{2}}}$

La funzione di trasferimento è data

$A(\omega )={\frac {R_{0}}{i\omega L+R_{0}}}$

Il punto 3 dB si ha quando ωL = R₀ così i 3 dB di cut-off è dato da

$\omega _{c}={\frac {R_{0}}{L}}$

dove ω è nella banda eliminata circa ω_c,

$A(\omega )\approx {\frac {R_{0}}{i\omega L}}$

può essere visto da A(ω) calando lontano nell abanda eliminata a 6 dB/ottava (o 20 dB/decade).

Passa alto

Z e Z' per un Zobel passa alto

Per un filtro passa alto, Z è una capacità e Z' un induttore:

$Z={\frac {1}{i\omega C}}$

e

$Z'=i\omega L'\!\,$

dove

$L'=CR_{0}^{2}\!\,$

La funzione di trasferimento della sezione è data da

$A(\omega )={\frac {i\omega CR_{0}}{1+i\omega CR_{0}}}$

Il punto 3 dB occorre quando ωC = ¹⁄_R0 così la frequenza a 3 dB cut-off è data da

$\omega _{c}={\frac {1}{CR_{0}}}$

In elimina banda,

$A(\omega )\approx i\omega CR_{0}$

Passa banda

Z and Z'  per un Zobel passa banda

Per una sezione passa banda, Z è una serie di circuiti risonanti e Z' è un o shunt risonante;

$Z=i\omega L+{\frac {1}{i\omega C}}$

e

$Y'={\frac {1}{Z'}}=i\omega C'+{\frac {1}{i\omega L'}}$

La funzione di trasferimento è data da

$A(\omega )={\frac {i\omega CR_{0}}{1+i\omega CR_{0}-\omega ^{2}LC}}$

Il punto 3 dB occorre quando |1 − ω²LC| = ωCR₀ così la frequenza a 3 dB cut-off è data da

$\omega _{c}={\frac {1}{2LC}}\left(\pm R_{0}C+{\sqrt {R_{0}^{2}C^{2}+4LC}}\right)$

dal centro frequenza, ω_m, e larghezza di banda, Δω, può essere determinata:

${\begin{aligned}\Delta \omega &={\frac {R_{0}}{L}}\\\omega _{m}&={\sqrt {{\frac {R_{0}^{2}}{4L^{2}}}+{\frac {1}{LC}}}}\end{aligned}}$

Nota questo è differente dalla frequenza di risonanza

$\omega _{0}={\sqrt {\frac {1}{LC}}}$

la relazione tra loro inizia da

$\omega _{m}^{2}=\left({\frac {\Delta \omega }{2}}\right)^{2}+\omega _{0}^{2}$

Elimina banda

Z and Z'  per un Zobel elimina banda

Per una sezione elimina banda, Z è uno shunt risonante e Z' è una serie risonante

$Y={\frac {1}{Z}}=i\omega C+{\frac {1}{i\omega L}}$

e

$Z'=i\omega L'+{\frac {1}{i\omega C'}}$

La funzione di trasferimento e la larghezza di banda può essere trovata in analogia con la sezione passa banda.

$\Delta \omega ={\frac {1}{CR_{0}}}$

e,

$\omega _{m}={\sqrt {\left({\frac {1}{2R_{0}C}}\right)^{2}+{\frac {1}{LC}}}}$

Voci correlate

• Otto Julius Zobel
• Filtro (elettronica)
• Impedenza immagine
• Filtro a costante k
• Cella di Boucherot
• Equalizzatore dei ritardi con ponte a T

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file su Rete zobel