Teorema di Morley

Il teorema di Morley afferma che se ogni angolo del triangolo viene diviso in tre parti uguali da due trisettrici, allora il triangolo in viola è un triangolo equilatero.

In geometria, il teorema di Morley stabilisce che i punti di intersezione delle coppie di trisettrici degli angoli adiacenti allo stesso lato di un qualsiasi triangolo, sono i vertici di un triangolo equilatero, chiamato "primo triangolo di Morley" o più semplicemente "triangolo di Morley". Tale teorema fu enunciato per la prima volta nel 1899 dal matematico anglo-americano Frank Morley. Il teorema, chiamato anche "miracolo di Morley", per la sua generalità e semplicità, è stato oggetto poi di varie generalizzazioni, una delle quali mostra in particolare che, se tutte le trisecanti si intersecano, si ottengono altri quattro triangoli equilateri.
Il teorema di Morley è valido solo nell'ambito della geometria euclidea e non sussiste quindi né in quella sferica né in quella iperbolica.

Dimostrazioni

Esistono molte dimostrazioni del teorema di Morley che utilizzano tecniche che vanno dalla geometria elementare, come nel caso della dimostrazione data da John Conway, in cui, a partire da un triangolo equilatero, si costruisce un altro triangolo che, alla fine, si può rendere simile a un triangolo qualsiasi (e il triangolo equilatero di partenza costituisce il suo triangolo di Morley), all'uso della trigonometria, all'utilizzo dei numeri complessi.

Dimostrazione trigonometrica

Fig 1.   Dimostrazione elementare del teorema di Morley.

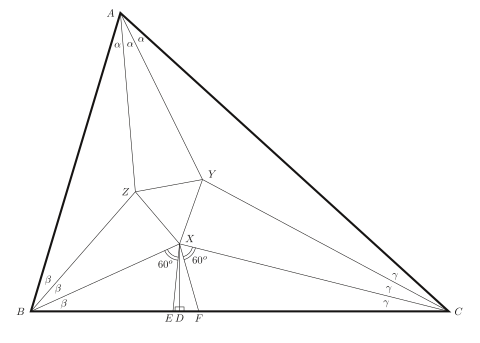
Una delle dimostrazioni che si avvalgono della trigonometria parte dalla seguente identità:

$\sin(3\theta )=4\sin \theta \sin(60^{\circ }+\theta )\sin(120^{\circ }+\theta )$

[1]

che, applicando la formula di addizione del seno, si può dimostrare essere uguale a quest'altra identità:

$\sin(3\theta )=-4\sin ^{3}\theta +3\sin \theta .$

La quale a sua volta può essere verificata applicando due volte la formula di addizione del seno al primo membro e poi utilizzando la formula :$\cos ^{2}\theta =1-\sin ^{2}\theta$ per sostituire la funzione coseno.

Osservando la figura 1, si vede che sul lato ${\overline {BC}}$ sono stati presi i punti $D,E,F$, e che, dato che la somma degli angoli interni di ogni triangolo è 180°, $3\alpha +3\beta +3\gamma =180^{\circ }$, da cui $\alpha +\beta +\gamma =60^{\circ }.$ Da questo consegue che gli angoli del triangolo $XEF$ sono $\alpha ,(60^{\circ }+\beta ),$ e $(60^{\circ }+\gamma ).$

Dalla figura 1 si vede anche che:

$\sin(60^{\circ }+\beta )={\frac {\overline {DX}}{\overline {XE}}}$

[2]

e

$\sin(60^{\circ }+\gamma )={\frac {\overline {DX}}{\overline {XF}}}.$

[3]

Inoltre,

${\hat {AYC}}=180^{\circ }-\alpha -\gamma =120^{\circ }+\beta$

e

${\hat {AZB}}=120^{\circ }+\gamma .$

[4]

Applicando il teorema dei seni ai triangoli $AYC$ e $AZB$ si ottiene

$\sin(120^{\circ }+\beta )={\frac {\overline {AC}}{\overline {AY}}}\sin \gamma$

[5]

e

$\sin(120^{\circ }+\gamma )={\frac {\overline {AB}}{\overline {AZ}}}\sin \beta .$

[6]

L'altezza del triangolo $ABC$ può essere espressa, utilizzando l'equazione [1] per sostituire $\sin(3\beta )$ e $\sin(3\gamma )$, in due modi:

$h={\overline {AB}}\sin(3\beta )={\overline {AB}}\cdot 4\sin \beta \sin(60^{\circ }+\beta )\sin(120^{\circ }+\beta )$

e

$h={\overline {AC}}\sin(3\gamma )={\overline {AC}}\cdot 4\sin \gamma \sin(60^{\circ }+\gamma )\sin(120^{\circ }+\gamma ).$

Utilizzando ora le equazioni [2] e [5] nell'equazione della $\beta$ e le equazioni [3] e [6] in quella della $\gamma$, si ottiene:

$h=4{\overline {AB}}\sin \beta \cdot {\frac {\overline {DX}}{\overline {XE}}}\cdot {\frac {\overline {AC}}{\overline {AY}}}\sin \gamma$

e

$h=4{\overline {AC}}\sin \gamma \cdot {\frac {\overline {DX}}{\overline {XF}}}\cdot {\frac {\overline {AB}}{\overline {AZ}}}\sin \beta$

Poiché i numeratori sono uguali:

${\overline {XE}}\cdot {\overline {AY}}={\overline {XF}}\cdot {\overline {AZ}}$

o

${\frac {\overline {XE}}{\overline {XF}}}={\frac {\overline {AZ}}{\overline {AY}}}.$

Poiché l'angolo $EXF$ e l'angolo $ZAY$ sono congruenti e i lati che formano questi angoli sono proporzionali, allora i triangoli $XEF$ e $AZY$ sono simili.

Ne consegue quindi che gli angoli $AYZ$ e $XFE$ sono congruenti e uguali a $(60^{\circ }+\gamma )$, mentre gli angoli $AZY$ e $XEF$ sono congruenti e uguali a $(60^{\circ }+\beta ).$ Allo stesso modo si possono ricavare gli angoli alla base per i triangoli $BXZ$ e $CYX.$

In particolare si trova che l'angolo $BZX$ è pari a $(60^{\circ }+\alpha )$ e, sempre dalla figura 1, si vede che:

${\hat {AZY}}+{\hat {AZB}}+{\hat {BZX}}+{\hat {XZY}}=360^{\circ }.$

Sostituendo in base a quanto sopra detto e utilizzando l'equazione [4] per l'angolo $AZB$ si ottiene:

$(60^{\circ }+\beta )+(120^{\circ }+\gamma )+(60^{\circ }+\alpha )+{\hat {XZY}}=360^{\circ }$

e quindi:

${\hat {XZY}}=60^{\circ }.$

Allo stesso modo si trova che anche gli altri due angoli del triangolo $XYZ$ hanno un valore di $60^{\circ }$ e quindi che il triangolo $XYZ$ è un triangolo equilatero.

Lato e area

Il primo triangolo di Morley ha lati di lunghezza pari a:

$a^{\prime }=b^{\prime }=c^{\prime }=8R\sin(A/3)\sin(B/3)\sin(C/3),\,$

dove R è il circumraggio del triangolo di partenza e ${\hat {A}},{\hat {B}}$ e ${\hat {C}}$ sono gli angoli di tale triangolo. Poiché l'area di un triangolo equilatero è espressa dalla formula ${\tfrac {\sqrt {3}}{4}}a'^{2},$ l'area del triangolo di Morley può essere espressa come:

${\text{Area}}=16{\sqrt {3}}R^{2}\sin ^{2}(A/3)\sin ^{2}(B/3)\sin ^{2}(C/3).$

Triangoli di Morley

Questa figura mostra i 18 triangoli di Morley di un dato triangolo ABC. Le sei coppie di trisecanti presenti ai tre angoli del triangolo sono disegnate e colorate in modo tale che le intersezioni di due secanti dello stesso colore identifichino 27 punti giacenti su 9 diversi segmenti, ognuno dei quali contiene 6 punti di intersezione, con tali segmenti che sono tra loro o paralleli o che formano un angolo di 60°.

Il teorema di Morley implica l'esistenza di 18 triangoli equilateri. Il triangolo sopra descritto nel teorema, chiamato primo triangolo di Morley, ha i vertici che, in coordinate trilineari relative al triangolo ABC, sono espressi come:

A-vertice = 1 : 2 cos(C/3) : 2 cos(B/3)

B-vertice = 2 cos(C/3) : 1 : 2 cos(A/3)

C-vertice = 2 cos(B/3) : 2 cos(A/3) : 1

Un altro dei triangoli equilateri di Morley, anch'esso un triangolo centrale, chiamato secondo triangolo di Morley ha invece i vertici espressi come:

A-vertice = 1 : 2 cos(C/3 − 2π/3) : 2 cos(B/3 − 2π/3)

B-vertice = 2 cos(C/3 − 2π/3) : 1 : 2 cos(A/3 − 2π/3)

C-vertice = 2 cos(B/3 − 2π/3) : 2 cos(A/3 − 2π/3) : 1

Il terzo dei 18 triangoli equilateri di Morley, anch'esso un triangolo centrale, chiamato terzo triangolo di Morley è dato dai seguenti vertici:

A-vertice = 1 : 2 cos(C/3 − 4π/3) : 2 cos(B/3 − 4π/3)

B-vertice = 2 cos(C/3 − 4π/3) : 1 : 2 cos(A/3 − 4π/3)

C-vertice = 2 cos(B/3 − 4π/3) : 2 cos(A/3 − 4π/3) : 1

I tre triangoli sopra descritti formano tra loro coppie omotetiche. Un altro triangolo a loro omotetico è formato da tre punti X presenti sulla circumcirconferenza del triangolo ABC e tali per cui la linea XX ⁻¹ è tangente al circumcerchio, dove X ⁻¹ denota il coniugato isogonale di X. Tale triangolo equilatero, chiamato triangolo circumtangenziale, ha i seguenti vertici:

A-vertice = csc(C/3 − B/3) : csc(B/3 + 2C/3) : −csc(C/3 + 2B/3)

B-vertice = −csc(A/3 + 2C/3) : csc(A/3 − C/3) : csc(C/3 + 2A/3)

C-vertice = csc(A/3 + 2B/3) : −csc(B/3 + 2A/3) : csc(B/3 − A/3)

Un quinto triangolo equilatero, anch'esso omotetico agli altri, si ottiene ruotando il triangolo circumtangenziale di ?/6 attorno al suo centro. Chiamato triangolo circumnormale, i suoi vertici possono essere espressi come:

A-vertice = sec(C/3 − B/3) : −sec(B/3 + 2C/3) : −sec(C/3 + 2B/3)

B-vertice = −sec(A/3 + 2C/3) : sec(A/3 − C/3) : −sec(C/3 + 2A/3)

C-vertice = −sec(A/3 + 2B/3) : −sec(B/3 + 2A/3) : sec(B/3 − A/3)

Attraverso un'operazione chiamata "extraversione" si può ottenere ognuno dei 18 triangoli di Morley da ognuno degli altri 18. Inoltre, ogni triangolo può essere "extravertito" in tre diversi modi, e i 18 triangoli di Morley assieme alle 27 coppie di triangoli extravertiti, formati i 18 vertici e le 27 facce di un grafo di Pappo.

Centri dei triangoli

Il baricentro del primo triangolo di Morley in coordinate trilineari è espresso come:

Centro di Morley = X(356) = cos(A/3) + 2 cos(B/3)cos(C/3) : cos(B/3) + 2 cos(C/3)cos(A/3) : cos(C/3) + 2 cos(A/3)cos(B/3).

Il primo triangolo di Morley è omologo al triangolo ABC: le linee che connettono un vertice del triangolo di partenza con il vertice opposto del triangolo di Morley si incontrano nel punto:

Primo centro di Morley–Taylor–Marr = X(357) = sec(A/3) : sec(B/3) : sec(C/3).

Altri progetti

Altri progetti

• Wikimedia Commons

• Wikimedia Commons contiene immagini o altri file su Teorema di Morley

Collegamenti esterni

• (EN) Eric W. Weisstein, Teorema di Morley, su MathWorld, Wolfram Research.