Topologia quoziente: differenze tra le versioni
Vai alla navigazione
Vai alla ricerca
Contenuto cancellato Contenuto aggiunto
m Inserimento automatico del portale matematica |
|||
| Riga 17: | Riga 17: | ||
== Esempi == |
== Esempi == |
||
*'''Incollamento.''' In topologia si costruiscono numerosi spazi per "incollamento". Se ''X'' è uno spazio topologico e due punti ''x'' e ''y'' di ''X'' vengono incollati, si costruisce lo spazio quoziente tramite la seguente semplice relazione di equivalenza: ''a ~ b'' se e solo se ''a = b'' oppure ''a = x, b = y'' (oppure ''a = y, b = x''). I due punti quindi diventano un punto solo. Ad esempio, in questo modo si può ottenere uno [[spazio connesso]] da uno avente due [[componente connessa|componenti connesse]]. |
*'''Incollamento.''' In topologia si costruiscono numerosi spazi per "incollamento". Se ''X'' è uno spazio topologico e due punti ''x'' e ''y'' di ''X'' vengono incollati, si costruisce lo spazio quoziente tramite la seguente semplice relazione di equivalenza: ''a ~ b'' se e solo se ''a = b'' oppure ''a = x, b = y'' (oppure ''a = y, b = x''). I due punti quindi diventano un punto solo. Ad esempio, in questo modo si può ottenere uno [[spazio connesso]] da uno avente due [[componente connessa|componenti connesse]]. |
||
:* In generale, se ''A'' è un sottoinsieme di uno spazio topologico ''X'', si costruisce uno spazio quoziente che "identifica ''A'' ad un solo punto" mediante la relazione di equivalenza ''a ~ b'' se e solo se ''a'' e ''b'' sono elementi di ''A''. Tale spazio viene talvolta indicato con ''X''/''A'' |
|||
*Consideriamo ''X'' = '''R''' l'insieme di tutti i [[numeri reali]], e poniamo ''x'' ~ ''y'' se e solo ''x''−''y'' è un [[intero]]. Lo spazio quoziente ''X''/~ è [[omeomorfo]] al [[cerchio]] ''S''<sup>1</sup> tramite la mappa che manda la classe di equivalenza di ''x'' su exp(2π''ix''). |
*Consideriamo ''X'' = '''R''' l'insieme di tutti i [[numeri reali]], e poniamo ''x'' ~ ''y'' se e solo ''x''−''y'' è un [[intero]]. Lo spazio quoziente ''X''/~ è [[omeomorfo]] al [[cerchio]] ''S''<sup>1</sup> tramite la mappa che manda la classe di equivalenza di ''x'' su exp(2π''ix''). |
||
*L'esempio precedente può essere esteso in dimensione arbitraria. Consideriamo ''X'' = '''R'''<sup>n</sup> e poniamo ''x ~ y'' se e solo se le ''i''-esime coordinate dei vettori ''x'' e ''y'' differiscono di un intero, per ogni ''i''. Lo spazio quoziente è omeomorfo al [[toro]] se ''n'' = 2, ed è chiamato ''toro ''n''-dimensionale'' per ''n'' qualsiasi. Il toro ''n''-dimensionale è omeomorfo al [[topologia prodotto|prodotto]] di ''n'' cerchi. |
*L'esempio precedente può essere esteso in dimensione arbitraria. Consideriamo ''X'' = '''R'''<sup>n</sup> e poniamo ''x ~ y'' se e solo se le ''i''-esime coordinate dei vettori ''x'' e ''y'' differiscono di un intero, per ogni ''i''. Lo spazio quoziente è omeomorfo al [[toro (geometria)|toro]] se ''n'' = 2, ed è chiamato ''toro ''n''-dimensionale'' per ''n'' qualsiasi. Il toro ''n''-dimensionale è omeomorfo al [[topologia prodotto|prodotto]] di ''n'' cerchi. |
||
*La [[bottiglia di Klein]] può essere ottenuta quozientando il [[toro]] tramite una opportuna relazione di equivalenza. |
*La [[bottiglia di Klein]] può essere ottenuta quozientando il [[toro (geometria)|toro]] tramite una opportuna relazione di equivalenza. |
||
*Il [[nastro di Möbius]] può essere ottenuto quozientando l'[[anello (topologia)|anello]] tramite una opportuna relazione di equivalenza. |
*Il [[nastro di Möbius]] può essere ottenuto quozientando l'[[anello (topologia)|anello]] tramite una opportuna relazione di equivalenza. |
||
*Lo [[spazio proiettivo]] è ottenuto quozientando uno [[spazio vettoriale]] |
*Lo [[spazio proiettivo]] è ottenuto quozientando uno [[spazio vettoriale]] privato dell'origine tramite la relazione seguente: ''x ~ y'' se e solo se ''x'' e ''y'' sono multipli (cioè stanno sulla stessa retta). |
||
== Proprietà == |
== Proprietà == |
||
Versione delle 15:39, 24 dic 2007
In topologia, la topologia quoziente è intuitivamente quella ottenuta da uno spazio topologico "attaccando" alcuni punti fra loro. Lo spazio topologico che si ottiene viene anche chiamato spazio quoziente.
Definizione
Sia X uno spazio topologico e ~ una relazione di equivalenza su X. Definiamo una topologia sull'insieme quoziente X/~ (che consiste di tutte le classi di equivalenza di ~) nel modo seguente: un insieme di classi di equivalenze in X/~ è aperto se e solo se la loro unione è aperta in X.
Sia q : X → X/~ la proiezione che manda ogni elemento di X nella sua classe. Elenchiamo alcune definizioni equivalenti di topologia quoziente sull'insieme X/~:
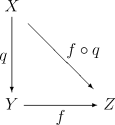
- Un insieme in X/~ è aperto se e solo se lo è la sua controimmagine tramite q in X.
- La topologia su X/~ è la più fine fra tutte quelle che rendono la mappa q continua.
- La topologia su X/~ è l'unica che soddisfi la seguente proprietà universale: se g : X → Z è una funzione continua tale che a~b implica g(a)=g(b) per ogni a e b in X, allora esiste una unica funzione continua f : X/~ → Z tale che g = f o q.
Nell'ultima definizione, diciamo che g scende al quoziente.
Esempi
- Incollamento. In topologia si costruiscono numerosi spazi per "incollamento". Se X è uno spazio topologico e due punti x e y di X vengono incollati, si costruisce lo spazio quoziente tramite la seguente semplice relazione di equivalenza: a ~ b se e solo se a = b oppure a = x, b = y (oppure a = y, b = x). I due punti quindi diventano un punto solo. Ad esempio, in questo modo si può ottenere uno spazio connesso da uno avente due componenti connesse.
- In generale, se A è un sottoinsieme di uno spazio topologico X, si costruisce uno spazio quoziente che "identifica A ad un solo punto" mediante la relazione di equivalenza a ~ b se e solo se a e b sono elementi di A. Tale spazio viene talvolta indicato con X/A
- Consideriamo X = R l'insieme di tutti i numeri reali, e poniamo x ~ y se e solo x−y è un intero. Lo spazio quoziente X/~ è omeomorfo al cerchio S1 tramite la mappa che manda la classe di equivalenza di x su exp(2πix).
- L'esempio precedente può essere esteso in dimensione arbitraria. Consideriamo X = Rn e poniamo x ~ y se e solo se le i-esime coordinate dei vettori x e y differiscono di un intero, per ogni i. Lo spazio quoziente è omeomorfo al toro se n = 2, ed è chiamato toro n-dimensionale per n qualsiasi. Il toro n-dimensionale è omeomorfo al prodotto di n cerchi.
- La bottiglia di Klein può essere ottenuta quozientando il toro tramite una opportuna relazione di equivalenza.
- Il nastro di Möbius può essere ottenuto quozientando l'anello tramite una opportuna relazione di equivalenza.
- Lo spazio proiettivo è ottenuto quozientando uno spazio vettoriale privato dell'origine tramite la relazione seguente: x ~ y se e solo se x e y sono multipli (cioè stanno sulla stessa retta).
Proprietà
- Se X è connesso, anche X/~ lo è.
- Se X è compatto, anche X/~ lo è.
- Se X soddisfa qualche assioma di separazione, lo spazio quoziente X/~ può non soddisfarlo. Ad esempio, X/~ è T1 se e solo se ogni classe di equivalenza di ~ è chiusa in X.
