Regola di selezione
In chimica e fisica, le regole di selezione sono condizioni che gli stati iniziale e finale di un sistema devono soddisfare affinché tra di essi possa verificarsi una transizione energetica. Possono pertanto essere anche chiamate "regole di transizione".
Le regole di transizione variano in funzione della tecnica utilizzata per osservare la transizione, che può essere di tipo elettronico, vibrazionale o rotazionale.
Esse vengono ricavate da una trattazione quantistica del sistema e in particolare da relazioni matematiche che devono verificarsi per l'applicazione di operatori, specifici della spettroscopia considerata, sulle funzioni d'onda che descrivono gli stati del sistema. Particolarmente degno di nota è il ruolo assunto dal vettore momento di dipolo di transizione.
Per la spettroscopia elettronica, ad esempio, le regole di selezione sono:
- regola di selezione di parità o regola di Laporte, per cui vale oppure
- regola di selezione di spin, per cui vale
- regola di selezione di simmetria.
È però da rimarcare il fatto che alcune transizioni teoricamente proibite possono verificarsi nella pratica comune, seppure talvolta con intensità davvero modesta, in seguito a variazioni flussionali di simmetria o ad accoppiamento vibronico.
Trattazione generale[modifica | modifica wikitesto]
In meccanica quantistica la base per una regola di selezione spettroscopica è il valore dell'integrale del momento di transizione[1]
- ,
dove e sono le funzioni d'onda dei due stati coinvolti nella transizione e μ è l'operatore del momento di transizione. Se il valore di questo integrale è zero, allora la transizione è proibita. In pratica non è necessario calcolare l'integrale per determinare la regola di selezione; è sufficiente determinare la simmetria della funzione del momento di transizione . Se la simmetria di questa funzione copre la rappresentazione totalsimmetrica del gruppo puntuale al quale appartiene la molecola o l'atomo, allora il suo valore in generale non sarà nullo e la transizione è permessa. Altrimenti la transizione è proibita.
L'integrale del momento di transizione è uguale a zero se la funzione del momento di transizione, , è antisimmetrica o dispari, cioè vale y(x) = -y(-x). La simmetria della funzione momento di transizione è il prodotto diretto delle parità dei suoi tre componenti. Le caratteristiche di simmetria di ciascun componente possono essere ottenute da una tabella dei caratteri che in genere contiene anche le regole per ottenere le simmetrie di un prodotto diretto.[2]
| Tipo di transizione | μ si trasforma in | note |
|---|---|---|
| Dipolo elettrico | x, y, z | Spettri ottici |
| Quadrupolo elettrico | x2, y2, z2, xy, xz, yz | Limitazioni x2 + y2 + z2 = 0 |
| Polarizzabilità elettrica | x2, y2, z2, xy, xz, yz | Spettri Raman |
| Dipolo magnetico | Rx, Ry, Rz | Spettri ottici (debole) |
Esempi[modifica | modifica wikitesto]
Spettri elettronici[modifica | modifica wikitesto]
La regola di Laporte è una regola di selezione che formalmente stabilisce che "in un ambiente centrosimmetrico, le transizioni tra orbitali atomici simili come s-s,p-p, d-d, o f-f, sono proibite". La regola di Laporte si applica alle transizioni di dipolo elettrico, per cui l'operatore ha simmetria u (dal tedesco ungerade, dispari).[3] Gli orbitali p hanno simmetria u, per cui la simmetria della funzione momento di transizione è data dal prodotto triplo u×u×u, che ha simmetria u. Le transizioni sono pertanto proibite. Parimenti, gli orbitali d hanno simmetria g, per cui il prodotto triplo g×u×g ha ancora simmetria u e la transizione è proibita.[4]
La funzione d'onda di un singolo elettrone è il prodotto spazio-dipendente della funzione d'onda spaziale e delle funzioni di spin. Lo spin è direzionale e ha parità dispari. Ne consegue che le transizioni in cui lo spin dovrebbe cambiare direzione sono proibite. In termini formali, solamente stati con lo stesso numero quantico di spin totale sono spin-permessi.[5]
Nella teoria del campo cristallino, le transizioni d-d che sono spin-probite sono molto più deboli di quelle spin-permesse. Entrambe possono essere osservate, nonostante la regola di Laporte, perché le transizioni sono accoppiate alle vibrazioni, che sono antisimmetriche e hanno la stessa simmetria dell'operatore momento di dipolo.[6]
Spettri vibrazionali[modifica | modifica wikitesto]
In spettroscopia vibrazionale, le transizioni si osservano tra differenti stati vibrazionali. In una vibrazione fondamentale, la molecola viene eccitata dal suo stato fondamentale (v = 0) al primo stato eccitato (v = 1). La simmetria della funzione d'onda dello stato fondamentale è la stessa di quella della molecola. È perciò la base per la rappresentazione totalsimmetrica nel gruppo puntuale della molecola. Ne consegue che, perché una transizione vibrazionale sia permessa, la simmetria della funzione d'onda dello stato eccitato deve essere la stessa della simmetria dell'operatore momento di transizione.[7]
Nella spettroscopia infrarossa, l'operatore momento di transizione trasforma sia come x che come y e z. Anche la funzione d'onda dello stato eccitato deve trasformare come almeno uno di questi vettori. Nella spettroscopia Raman, l'operatore trasforma come uno dei termini di secondo grado nella colonna più a destra della sottostante tabella dei caratteri.[2]
| E | 8 C3 | 3 C2 | 6 S4 | 6 σd | |||
| A1 | 1 | 1 | 1 | 1 | 1 | x2 + y2 + z2 | |
| A2 | 1 | 1 | 1 | -1 | -1 | ||
| E | 2 | -1 | 2 | 0 | 0 | (2 z2 - x2 - y2,x2 - y2) | |
| T1 | 3 | 0 | -1 | 1 | -1 | (Rx, Ry, Rz) | |
| T2 | 3 | 0 | -1 | -1 | 1 | (x, y, z) | (xy, xz, yz) |
La molecola del metano, CH4, può essere usata come esempio per illustrare l'applicazione di questi principi. La molecola è tetraedrica e ha simmetria Td. Le vibrazioni del metano coprono le rappresentazioni A1 + E + 2T2.[8] L'esame della tabella dei caratteri mostra che tutte e quattro le vibrazioni sono Raman attive, ma solo le vibrazioni T2 sono visibili nello spettro infrarosso.[9]
Nell'approssimazione dell'oscillatore armonico quantistico, gli ipertoni sono proibiti sia negli spettri infrarossi che Raman. Tuttavia se si tiene conto dell'anarmonicità, le transizioni sono debolmente ammesse.[10]
Spettri rotazionali[modifica | modifica wikitesto]
La regola di selezione per le transizioni rotazionali, derivate dalle simmetrie delle funzioni d'onda rotazionali in un rotatore rigido, è ΔJ = ±1, dove J è il numero quantico rotazionale.[11]
Transizioni accoppiate[modifica | modifica wikitesto]
Ci sono molti tipi di transizioni accoppiate, come si può osservare negli spettri roto-vibrazionali. La funzione d'onda dello stato eccitato è il prodotto di due funzioni d'onda, ad esempio vibrazionale e rotazionale. Il principio generale è che la simmetria dello stato eccitato si ottiene come prodotto diretto delle simmetrie delle funzioni d'onda componenti.[12] Nelle transizioni rotovibrazionali, gli stati eccitati coinvolgono tre funzioni d'onda.
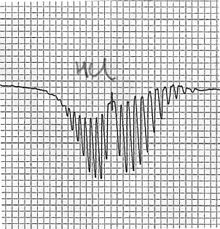
Lo spettro infrarosso dell'acido cloridrico gassoso mostra la struttura fine rotazionale sovraimposta allo spettro vibrazionale. Questo è tipico degli spettri infrarossi delle molecole eteronucleari. Sono presenti i rami P eR, mentre il ramo Q, situato alla frequenza di vibrazione, è assente. Questo ramo è presente nelle molecole a simmetria sferica, come consegue dall'applicazione delle regole di selezione.[13]
La spettroscopia Raman di risonanza coinvolge una sorta di accoppiamento rotovibrazionale. Ne risulta un'accresciuta intensità delle transizioni fondamentali e degli ipertoni, poiché le vibrazioni sottraggono energia da una transizione elettronica permessa.[14] Nonostante le apparenze, le regole di selezione sono le stesse della spettroscopia Raman.[15]
Momento angolare[modifica | modifica wikitesto]
- Vedi anche Interazione spin-orbita
In generale una radiazione elettrica (carica) o magnetica (corrente, momento magnetico) può essere classificata in multipoli Eλ (elettrico) o Mλ (magnetico) di ordine 2λ, ad esempio E1 per il dipolo elettrico, E2 per il quadrupolo o E3 per l'ottupolo. Nelle radiazioni in cui la variazione del momento angolare tra lo stato iniziale e quello finale rende possibili molte radiazioni di multipolo, di solito i multipoli di ordine più basso sono predominantemente più probabili e dominano la transizione.[16]
La particella emessa porta con sé un momento angolare λ, che per il fotone deve essere almeno 1, dal momento che è una particella vettore (cioè possiede un numero quantico di momento angolare totale JP = 1−). Non c'è quindi né un monopolo elettrico E0 né un monopolo magnetico M0.
Poiché il momento angolare totale deve essere conservato durante la transizione, si ha che
dove , la sua z-proiezione è data da ; e sono, rispettivamente, il momento angolare iniziale e finale dell'atomo. I corrispondenti numeri quantici λ e μ (momento angolare dell'asse z) devono soddisfare
e
La parità è conservata. Per le transizioni di multipolo elettrico
mentre per i multipoli magnetici
Pertanto la parità non cambia per multipoli E-pari o M-dispari, mentre cambia per multipoli E-dispari o M-pari.
Queste considerazioni generano differenti serie di regole di transizione che dipendono dal tipo e dall'ordine del multipolo. Quando si utilizza l'espressione linea proibita, non significa che queste transizioni non possano avvenire, ma che sono dipolo elettrico-proibite. Sono pertanto possibili, ma con tassi poco elevati.
Se la probabilità di una transizione E1 non è nulla, la transizione è permessa; se invece è zero, allora le transizioni come M1, E2 possono produrre una radiazione, ma con tassi di transizione molto bassi per cui vengono definite frequenze proibite. Il tasso di transizione decresce di un fattore 1000 nel passare da un multipolo al successivo, cosicché le transizioni dei multipoli più bassi sono le più probabili.[17]
Le transizioni semi-proibite (che danno luogo alle cosiddette linee di intercombinazione) sono le transizioni di dipolo elettrico E1 per le quali viene violata la regola di transizione che richiede che lo spin non deve variare. Deriva dal fallimento dell'interazione spin-orbita.
Tabella riassuntiva[modifica | modifica wikitesto]
Nella tabella viene utilizzata la seguente simbologia:
- è il momento angolare totale,
- è il numero quantico orbitale,
- è il numero quantico di spin,
- è il numero quantico secondario del momento angolare totale.
Le transizioni ammesse sono quelle basate sull'atomo idrogenoide. Il simbolo indica una transizione proibita.
| Transizioni permesse | Dipolo elettrico (E1) | Dipolo magnetico (M1) | Quadrupolo elettrico (E2) | Quadrupolo magnetico (M2) | Ottupolo elettrico (E3) | Ottupolo magnetico (M3) | |
|---|---|---|---|---|---|---|---|
| Regole rigorose | (1) | ||||||
| (2) | |||||||
| (3) | |||||||
| Accoppiamento LS | (4) | Un salto elettronico Δl = ±1 |
Nessun salto elettronico Δl = 0, Δn = 0 |
Nessuno o un salto elettronico Δl = 0, ±2 |
Un salto elettronico Δl = ±1 |
Un salto elettronico Δl = ±1, ±3 |
Un salto elettronico Δl = 0, ±2 |
| (5) | Se ΔS = 0 |
Se ΔS = 0 |
Se ΔS = 0 |
Se ΔS = 0 | |||
| Accoppiamenti intermedi | (6) | Se ΔS = ±1 |
Se ΔS = ±1 |
Se ΔS = ±1 |
Se ΔS = ±1 |
Se ΔS = ±1 | |
Superficie[modifica | modifica wikitesto]
Nella spettroscopia vibrazionale, si applica la regola di selezione di superficie per identificare i picchi osservati negli spettri vibrazionali. Quando una molecola viene adsorbita da un substrato, la molecole induce una carica immagine opposta nel substrato. Il momento di dipolo della molecola e la carica immagine perpendicolare alla superficie si rinforzano reciprocamente. Invece il momento di dipolo della molecola e la carica immagine parallela alla superficie si eliminano. Di conseguenza, solo i picchi molecolari vibrazionali che danno origine a un momento di dipolo dinamico perpendicolare alla superficie possono essere osservati nello spettro vibrazionale.
Note[modifica | modifica wikitesto]
- ^ Harris & Berolucci, p. 130
- ^ a b c J.A. Salthouse e Ware, M.J., Point group character tables and related data, Cambridge University Press, 1972, ISBN 0-521-08139-4.
- ^ Una simmetria u è antisimmetrica rispetto al centro di simmetria. Il tipo g (dal tedesco gerade, pari) invece indica simmetria rispetto al centro di simmetria. Se la funzione momento di transizione ha simmetria u, le parti positive e negative saranno uguali l'una all'altra, cosicché l'integrale ha valore zero.
- ^ Harris & Berolucci, p. 330
- ^ Harris & Berolucci, p. 336
- ^ Cotton Section 9.6, Selection rules and polarizations
- ^ Cotton, Section 10.6 Regole di selezione per le transizioni vibrazionali fondamentali.
- ^ Cotton, Chapter 10 Molecular Vibrations
- ^ Cotton p. 327
- ^ S. Califano, Vibrational states, Wiley, 1976, ISBN 0-471-12996-8. Chapter 9, Anharmonicity
- ^ H.W. Kroto, Molecular Rotation Spectra, new York, Dover, 1992, ISBN 0-486-49540-X.
- ^ Harris & Berolucci, p. 339
- ^ Harris & Berolucci, p. 123
- ^ D.A. Long, The Raman Effect: A Unified Treatment of the Theory of Raman Scattering by Molecules, Wiley, 2001, ISBN 0-471-49028-8. Chapter 7, Vibrational Resonance Raman Scattering
- ^ Harris & Berolucci, p. 198
- ^ T.P. Softley, Atomic Spectra, Oxford, Oxford University Press, 1994, ISBN 0-19-855688-8.
- ^ E.V. Condon e Shortley, G.H., The Theory of Atomic Spectra, Cambridge University Press, 1953, ISBN 0-521-09209-4.
Bibliografia[modifica | modifica wikitesto]
- D.C. Harris e Bertolucci, M.D., Symmetry and Spectroscopy, Oxford University Press, 1978, ISBN 0-19-855152-5.
- F.A. Cotton, Chemical Applications of Group Theory, 3rd, Wiley, 1990, ISBN 978-0-471-51094-9.
- L. Stanton, Selection rules for pure rotation and vibration-rotation hyper-Raman spectra, in Journal of Raman Spectroscopy, vol. 1, n. 1, 1973, pp. 53–70, Bibcode:1973JRSp....1...53S, DOI:10.1002/jrs.1250010105.
- D.I Bower e Maddams, W.F., The vibrational spectroscopy of polymers, Cambridge University Press, 1989, ISBN 0-521-24633-4. Section 4.1.5: Selection rules for Raman activity.
- P.M.A. Sherwood, Vibrational Spectroscopy of Solids, Cambridge University Press, 1972, ISBN 0-521-08482-2. Chapter 4: The interaction of radiation with a crystal.
- J.A. Salthouse, Ware, M.J., Point group character tables and related data. Cambridge University Press, 1972, ISBN 0521081394.
- Pierre Meystre, Murray Sargent, Element of Quantum Optics. 4ª ediz. Springer, Berlin/Heidelberg/New York 2007, ISBN 9783540742098.
- Christopher C. Gerry, Peter L. Knight, Introductory Quantum Optics. 3ª ediz. Cambridge University Press, Cambridge 2008, ISBN 9780521527354.
Collegamenti esterni[modifica | modifica wikitesto]
- National Institute of Standards and Technology, su physics.nist.gov. URL consultato il 17 giugno 2015 (archiviato dall'url originale il 14 maggio 2011).
- University of Oxford - Lecture Notes - Atomic Physics B1 (PDF), su physics.ox.ac.uk.
- Lecture notes from The University of Sheffield (PDF), su shef.ac.uk. URL consultato il 17 giugno 2015 (archiviato dall'url originale il 26 aprile 2005).




































